 |
3. Пост электр поле: потенциал и градиент потенциала в поле точечн ист-ка.
|
|
|
|
3. Пост электр поле: потенциал и градиент потенциала в поле точечн ист-ка.
Постоянное эл. поле применяют в неск-их методах э. р: ВЭЗ, ВП, ЭП, МЗ и др. Его возбуждают в З. гальваническим способом с помощью заземленного кабеля, к кот подведено питание от источника постоян. тока (генератора, аккумуляторов, сухих батарей). В настоящее время вместо постоян. поля чаще стали использовать перемен. поле низкой частоты, поскольку в постоян. поле труднее избавл-ся от полей-помех. Однако в перечислен. методах используют теорию постоян. поля: расчет коэффициентов установки, решение пр. и обр. задач и др. вопросы.
В случае пост эл поля ур-е Максвелла: divD=0, divB=0, rotE=0, rotH=j
div rot H = div j, div j=0 (з. Кирхгофа 1ый) –расход-ть пл-ти тока в люб точке среды, j=1/ρ *E; div 1/ρ *E =0; 1/ρ x dEx/dx+ 1/ρ y dEy/dy +1/ρ z dEz/ dz =0 (одн аниз среда)
Потенциал –энергетич хар-ка эл поля, численно = работе по перемещению заряда из беск-ти в заданную точку. rot E= rot (+- grad U)=0
E=+- grad U связь напр-ти с потенциалом
В однородно изотр среде dEx/dx+ dEy/dy + dEz/ dz =0 ур-е Лапласса
Теория электроразв-х мет-в пост тока основана на использовании стационарной модели электромагнитного поля. В этом случае электрич поле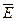 
является безвихревым и удовл-т ур-ю Лапласа. В теории поля показано, что векторная функция, удовлетворяющая этому уравнению, может быть однозначно описана скалярной функцией, называемой потенц-м. Переход от векторной хар-ки к скалярной упрощает решение многих задач. Скалярный потенциал 
связан с постоянным электрическим полем 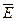соотношением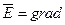 
,
Физически потенциал представляет собой работу, которую необходимо совершить в электрическом поле при переносе единичного положительного заряда из бесконечности в данную точку.
|
|
|
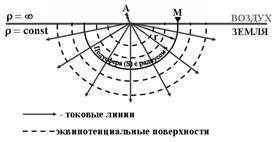Рис. Поле точ ист-ка пост тока, над однор разр-м.
Данная задача является простейшей задачей электр-ки постоянным током Пусть электрод А посылает в Землю ток силой I. Сопр-е воздуха бесконечно велико, поэтому весь ток растекается в Земле, имеющей сопр-е r. Земля однородна, следовательно, ток от источника течет равномерно по всем направлениям, т. е. линии плотности тока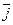 
представляют собой прямые лучи, исходящие из точки А. Окружим точку А полусферой S произвольного радиуса r с центром в точке А. Очевидно, что сила тока, проходящая через нее, равна полной силе тока I. След-но, плотность тока в любой точке M, располож на полусфере, равна силе тока, деленной на площадь полусферы: 
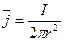, По закону Ома 
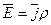, откуда, используя формулу, получим: 
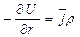. Теперь перейдем к формуле 
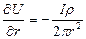Проинтегрировав это ур-е в пределах от ¥ до некот конкретного зн-я r, получ: 
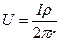: Итак, потенциал точечного ист-ка пропорционален силе тока I и сопр-ю r и обратно пропорц-н расстоянию до ист-ка r. Очевидно, что напр-ть эл поля, как производная потенциала, будет убывать при удалении от точечного ист-ка как 1/r2.
11. Понятие прямой и обратной задач элек-ки. Некорректность постановки обратных задач по Адамару и Тихонову.
Прямая задача –расчет элементов поля по заданным параметрам модели среды и положению ист-ков поля. Несмотря на слож-ть матем реализации имеет однозн реш-е.
Обратная задача – связана с определением строения и физического состояния геологической среды по значениям электрич поля, измерен на повер-ти или во внутренних точках среды (восстан-е внутр стр-ры среды по известному распределению элементов поля на ее поверхности).
Принадлежит к классу некор-х задач: неоднозначн выбор модели, влияние различн рода помех, кот в теории не всегда учтены. !!! Практическая недоопределенность обр задачи, приводящая к неоднозначн результату.
|
|
|
Усл-я корректно поставленной задачи впервые были сформ-ны Ж. Адамаром (1962г): задача считается корректно поставленной, •если априори известно, что ее решение существует, •оно единственно и •устойчиво к малым изменениям исходных данных (в противном случае плохо или некорректно поставленная).
Что касается метода эл зонд-й, то сущ-е реш-я задачи опр-ся ее физич детерминированность. Мат озм-ть получ-я единств решения для горизонтальнооднор сред оказ-ся теорема единственности ( Тихонов), из кот следует, что
•по точным значениям потенциала, заданным вдоль некоторой непрерывной прямой на поверхности наблюдения можно сделать единственно возможное закл-е об изменении проводимости с глубиной (на пр погр-ти, дискр изм-я, неуст-ть –некор!!! )
Способ регуляризации
ρ к(r)= ρ 1r∫ R1(m) J1(m) m dm
R1(m)=th (mh1+arth ρ 1/ρ 2 R2(m)); R2(m)=… Rn(m)=1
Рассмотрим горизонтально-слоистую среду: f=A*x, х (сов-ть исх пар-ов) принадл Х, f (изм-е поля) принадл F.
Отклон-е измерений поля и пар-ов модели среды inf||f-f’||=δ (нижн гр откл-я измер зн-я поля), inf||x-x’||= ε (точн-ть опр-я), А- нелин опреатор, связывает эл поле с пар-ми слоев в подинтегр выражении, неуст и неедин-ть реш-я –следствие его св-в.
Согл-но Тихонову в Х можно выделить более узкое пр-во М, для кот выпол-ся усл-е корректности, если априори изв-но, что принадлежащее М реш-е сущ-ет, оно единственно и уст к малым изм-м f. Для нее должна выполняться непрер зав-ть между погреш-тью набл-й и рез-м интер-и: lim x(δ à 0)=x’
При этом искомое зн-е должно выходить за пределы потери чувст-ти набл поля к изм-ю пар-в среды при заданной величине δ: rm=inf ||∆ f||F/||∆ x||X> C(δ )
Т. е. некор по Адамару мб корректн по Тихонову. Множ-во М (мн-во кор-ти) выбираем на основе доп инф-и. Для рег-и исп оператор, например, Ф(α, x)=||Az-f’||F2+α Ω (x)=min,
1 слаг мин-я расх-я м\ду набл и расч ф-ми, 2-минимизирует критерий отбора апр инф.
Т. о. суть регул-и –получение приближ реш-я обр задачи в рамках погр-ти, уст-го к малому изм-ю некор данных с помощью доп инф-и, вовлекаемой в процесс решения (физическое доопределение обр задачи).
Адаптивная регуляризация- позволяет детализ-ть расчленение разреза с информац возможностями анализируемого поля: исп логар масштаба; инт геоэл модели (мощность кажд слоя, больше предыдущего); обощ пар-ов (сумм прод пр-ть, сумм попер сопр-е)- более уст к малым изм-м исх данных.
|
|
|
|
|
|
