 |
10. Инт-я трехслойных и четырехслойных кривых МТЗ. Построение геоэлектрического разреза.
|
|
|
|
Конечный результат обработки полевых набл-й – кривые МТЗ (их строят на логарифмическом бланке, по x откл-т √ Т, а по y rТ. 
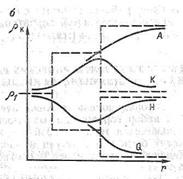 По виду или типу кривой зонд-я всегда можно опр-ть, какие породы — высокого или низкого удельного сопротивления — залегают под слоем наносов. Основной рабочей моделью при интерпретации кривых зондирования служит трехслойный геоэлектрический разрез, состоящий из двух слоев ограниченной мощности и подстилающего основания бесконечно большой мощности. Известны четыре типа трехслойных разрезов: тип А — р1< р2< р3, тип К— р1< р2> Рз, тип Н — р1> р2< рз, тип Q— р1> р2> р3. Соответствующие графики кажущихся сопротивлений, или кривые зондирования, также принято называть кривыми типа А, К, Н и Q.
По виду или типу кривой зонд-я всегда можно опр-ть, какие породы — высокого или низкого удельного сопротивления — залегают под слоем наносов. Основной рабочей моделью при интерпретации кривых зондирования служит трехслойный геоэлектрический разрез, состоящий из двух слоев ограниченной мощности и подстилающего основания бесконечно большой мощности. Известны четыре типа трехслойных разрезов: тип А — р1< р2< р3, тип К— р1< р2> Рз, тип Н — р1> р2< рз, тип Q— р1> р2> р3. Соответствующие графики кажущихся сопротивлений, или кривые зондирования, также принято называть кривыми типа А, К, Н и Q.
Кривые зондирования имеют левую, среднюю и правую ветви. Левая ветвь отражает соотношение удельных сопротивлений первых двух слоев, средняя характеризует в какой-то мере УЭС промежуточного слоя, правая — соотн-е УЭС 3го и 2го слоев. Правая ветвь, несет инф-ю об интегральных пар-х разреза: S, H и ρ L. На графике зонд-я, каж сопр-е изменяется от p1 до р3, отклоняясь в сторону макс или мин в зависимости от УЭС промежут слоя.
На кривых МТЗпри большой мощности 2го слоя образуются два экстремума, обусловленных наложением эффектов от двух промежуточных границ.
Модель трехслойной среды представляется универсальной в том смысле, что она позволяет имитировать эффекты от промеж слоя, ограниченного сверху и снизу породами иного удельного сопротивления. Эти эффекты проявляются на кривой зонд-я на фоне влияния выше- и нижележащих пород. Степень проявления эффектов от промежуточного слоя зависит от его мощности и удельного сопротивления.
|
|
|
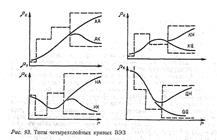 Различают восемь типов четырехслойного разреза: 1) АА—р1< p2< p3< p4, 2) АК—: р1< р2< р3> р4, 3) КН—р1< р2> р3< р4, 4) KQ—р1< р2> р3> р4, 5) НА—-р1> р2< р3< р4, 6) НК—р1> p2< p3> p4, 7) QQ—р1> p2> p3> р4, 8)QH —р1> р2 > p3< р4- Соответствующие им кривые зонд-я также им-ют кривыми типов АА, АК, КН, KQ, НА, НК, QQ, QH.
Различают восемь типов четырехслойного разреза: 1) АА—р1< p2< p3< p4, 2) АК—: р1< р2< р3> р4, 3) КН—р1< р2> р3< р4, 4) KQ—р1< р2> р3> р4, 5) НА—-р1> р2< р3< р4, 6) НК—р1> p2< p3> p4, 7) QQ—р1> p2> p3> р4, 8)QH —р1> р2 > p3< р4- Соответствующие им кривые зонд-я также им-ют кривыми типов АА, АК, КН, KQ, НА, НК, QQ, QH.
При благ-х геоэлек-х усл-х на них проявляются все слои разреза. В этом случае по типу кривой зонд-я можно качественно расчленить разрез и опр-ть послед-ть залегания пластов с различной электропроводностью. Чаще приходится встречаться с неясным типом кривых зонд-я, когда отдельные слои визуально не выделяются, хотя их влияние в какой-то-мере все же отр-ся на величине каж сопр-я. Т. о., по виду кривой зонд-я не всегда можно однозначно опр-ть тип разреза. Ошибки подобного рода иногда приводят к неправильному ист-ю рез-в полевых наблюдений.
При колич инт-и наблюденные кривые сравнивают с теорет, собранные в альбомы. Но в большинстве случаев не удается получить левые ветви кривых, связанные с высокими частотами поля (содержащие инф-ю о поверхностной части разреза). Поэтому инт-я осн-ся на исп-и правых ветвей, характ-х глубокие горизонты. Если оп горизонт обладает очень высоким сопр-м, правая ветвь имеет прямолинейную асимптоту, наклоненную к оси времен под углом 63025/.
 По этой асимптоте можно определить S надопорной толщи. Необходимо правую ветвь кривой продолжить до единичной оси, абсцисса точки пересечения TS(1-2) связана с параметром S:
По этой асимптоте можно определить S надопорной толщи. Необходимо правую ветвь кривой продолжить до единичной оси, абсцисса точки пересечения TS(1-2) связана с параметром S: 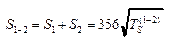 . Если опорный горизонт обл-т сопр-ем, кот сущ-но меньше сопр-я надопорной толщи, кривая МТЗ имеет правую асимптоту под углом 63025/, в этом случае можно опред-ть Н надопорной толщи:
. Если опорный горизонт обл-т сопр-ем, кот сущ-но меньше сопр-я надопорной толщи, кривая МТЗ имеет правую асимптоту под углом 63025/, в этом случае можно опред-ть Н надопорной толщи: 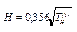 . По этим данным строят геоэлект разрез.
. По этим данным строят геоэлект разрез.
Привязку геоэл-х границ осущ-т визуально путем сопост-я рез-в зонд-я с данными бурения и ГИС. В зав-ти от сложности разреза применяют различ-е вар-ты совместной обработки.
|
|
|
Колич инт-ю кривых МТЗ в рамках модели ГСС выполняют с помощью следующих способов: 1) асимптотических; 2) алгебраических или дифференциальных трансформаций; 3) палеточных; 4) по координатам экстремальных точек; 5) методом подбора на ЭВМ.
Идея 1го состоит в том, что в случае опорного горизонта высокогоУЭС кривая T имеет восходящую ветвь, наклоненную под 63°. Проводя касательную к этой асимптоте по пересечению этой асимптоты с гориз линиями T=10 или T=1, можно определить величину S до высокоомного основания разреза.
Идея 2го состоит в преобразовании кривой 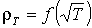 в кривую, как можно более близкую к ИСТИН=f (HИСТИН) или SИСТИН = f (HИСТИН).
в кривую, как можно более близкую к ИСТИН=f (HИСТИН) или SИСТИН = f (HИСТИН).
В основе 3го лежит графическое совмещение практических кривых МТЗ с теоретическими кривыми.. Многослойные кривые интер-ют по частям, используя принцип эквивалентных замен. Практические рез-ты интерпретации мб получены в пределах действия принципа экв-ти. Эти пределы практической неоднозн-ти в оценке параметров промежуточных слоев мб определены с помощью номограмм экв-ти Б. К. Матвеева. Установлено, что на переменном токе принцип экв-ти проявляется в более узких пределах, чем на постоянном токе. Кроме того, для разрезов типа K и Q вместо принципа экв-ти по Т2 на перем токе действует экв-ть по h2, то есть зн-е сопр-я промежут высокоомного слоя почти не влияет на оценку мощности этого слоя.
4ый интерпретации основан на теоретических и эксперимен-х связях координат характерных точек кривых МТЗ с параметрами разреза.
Интерпретация на ЭВМ наиболее распространена в Н. в.. С помощью ЭВМ параметры геоэлектрического разреза находятся путем минимизации функционала невязки: 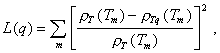 характеризующего среднеквадр отклонение эксперим кривой T от модельной кривой Tq. Минимизацию выполняют, корректируя параметры модели q. Нач значения q (нулевое приближение) выбирают с исп-м имеющейся геолого-геофизической информации.
характеризующего среднеквадр отклонение эксперим кривой T от модельной кривой Tq. Минимизацию выполняют, корректируя параметры модели q. Нач значения q (нулевое приближение) выбирают с исп-м имеющейся геолого-геофизической информации.
Определение S по МТЗ.
( N= ). В этом случае: 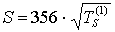 или
или 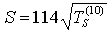 , где
, где 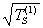 и
и 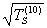 - абсциссы точки пересечения линии S с линиями Т=1 Ом·м и Т=10 Ом·м. Если кривая МТЗ имеет четкий мин, то величина S мб приближенно оценена как
- абсциссы точки пересечения линии S с линиями Т=1 Ом·м и Т=10 Ом·м. Если кривая МТЗ имеет четкий мин, то величина S мб приближенно оценена как 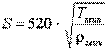
Определение удельного сопротивления опорного горизонта. Если восходящая ветвь кривой Т наклонена к оси абсцисс под углом 63°, то полагают, что N=. При меньших углах наклона восходящей ветви величину N оценивают путем кол интерпретации.
|
|
|
Определение среднего продольного сопротивления L надопорной толщи. В благоприятных условиях L может быть определено по ординате минимума кривой МТЗ L=P мин, где P - коэффициент, зависящий от соотношения параметров разреза.
В случае трехслойного разреза типа H может быть предложена более точная формула  , которая применима при известном 2. Значения q=1. 2 при 2=1-2 и q=1. 15 при 2> 2.
, которая применима при известном 2. Значения q=1. 2 при 2=1-2 и q=1. 15 при 2> 2.
Если на части кривых минимум не выражен, величина L может быть определена по корреляционной связи между нею и S. Формула Гуммеля говорит о линейной связи между этим величинами. Вместе с тем из-за логнормального распределения, которое, как известно, характерно для величин, применяемых в электроразведке, вполне возможен какой-то вариант линейной связи между логарифмами этих величин. Такую связь следует опробовать, если предположение о линейной связи L(S) приводит к противоречию с геологическими данными и здравым
Определение суммарной мощности H надопорной толщи. В случае опорного горизонта (основания разреза) высокого сопротивления, суммарная мощность надопорной толщи определяется по формуле Гуммеля 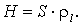 (размерность - метры). Для определения H (размерность - километры) используются также приближенные формулы Т. Н. Завадской
(размерность - метры). Для определения H (размерность - километры) используются также приближенные формулы Т. Н. Завадской  или Г. Д. Цекова
или Г. Д. Цекова 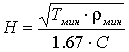 , где 2 - сопротивление второго слоя в разрезе типа H, а С - коэффициент, зависящий от 2 и 2: при 4, С=1, при 2< 4, 1< C< 2. 2.
, где 2 - сопротивление второго слоя в разрезе типа H, а С - коэффициент, зависящий от 2 и 2: при 4, С=1, при 2< 4, 1< C< 2. 2.
Мощность 1-го слоя высокого сопр-я В разрезах типа H (и А) эту величину находят по ниспадающей ветви кривой МТЗ. Если сопротивление подстилающего (2-го) проводящего слоя равно 0, то: 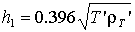 , где
, где  - абсцисса и ордината любой точки на ниспадающей под 63° амплитудной кривой МТЗ. В случае более пологой нисходящей ветви ( 2 не равно 0), мощность 1-го слоя можно оценить по двухточечной формуле Б. К. Матвеева:
- абсцисса и ордината любой точки на ниспадающей под 63° амплитудной кривой МТЗ. В случае более пологой нисходящей ветви ( 2 не равно 0), мощность 1-го слоя можно оценить по двухточечной формуле Б. К. Матвеева: 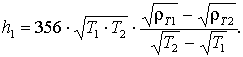 В разрезах типа H (и А) эту величину находят по ниспадающей ветви кривой МТЗ. Если сопротивление подстилающего (2-го) проводящего слоя равно 0, то:
В разрезах типа H (и А) эту величину находят по ниспадающей ветви кривой МТЗ. Если сопротивление подстилающего (2-го) проводящего слоя равно 0, то: 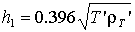 , где
, где  - абсцисса и ордината любой точки на ниспадающей под 63° амплитудной кривой МТЗ. В случае более пологой нисходящей ветви ( 2 не равно 0), мощность 1-го слоя можно оценить по двухточечной формуле Б. К. Матвеева:
- абсцисса и ордината любой точки на ниспадающей под 63° амплитудной кривой МТЗ. В случае более пологой нисходящей ветви ( 2 не равно 0), мощность 1-го слоя можно оценить по двухточечной формуле Б. К. Матвеева: 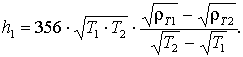
|
|
|
7. Способы вычисления высших производных. Достоинства и недостатки различных способов.
Для облегч-я реш-я теор задач в теорию грав-и был введен потенциал с. т. W. В т. А на расст-и ra от ц. З W=GM/ra, в т. в W=GM/(ra+∆ r). Разность потенц при малом ∆ r ∆ W=-GM∆ r/r2=
=-g∆ r –с. т. проив от потенциала по напр-ю к З. Проив-е W по 3м напр-я gx, gy, gz однозначно опр его полн вектор, если z направлена к центру З, dW/dx=dW/dy=0, dW/dz=g!!!!!!
В гравим-и изуч и вторые проивз-е, втор проив указ на ск-ть изм-я силы тяж-ти по осям (по х-гориз град-т с. т. ). Вторые произ-е хар-ют форму уров поверх-ти. Ед –Этвеш (10 в -9/с2) – изм-е с. т. в 0, 1 мГал на 1 км.
|
|
|


