 |
Кинетика кристаллизации стеклообразующих жидкостей.
|
|
|
|
Принципиальная возможность получения вещества в стеклообразном состоянии определяется величиной скорости кристаллизации: чем выше скорость кристаллизации переохлажденной жидкости, тем выше должна быть скорость охлаждения до стеклообразного состояния во избежание ее кристаллизации.
Процесс кристаллизации жидкости относится к фазовому переходу первого рода – т.е. это гетерогенный процесс. Возникновение новой кристаллической фазы в объеме старой не может происходить в результате непрерывного изменения структуры. В исходной системе можно выделить центры, в которых превращение прошло, а в остальной части – нет, т.е. можно определить и выделить области, за счет роста которых происходит увеличение доли объема, занимаемого превращенной фазой. Соответственно, имеют место два процесса, обусловливающих фазовое превращение: зарождение (зародышеобразование, нуклеация) и рост новой фазы.
Скорость образования центров кристаллизации (зародышей кристаллов).
Считается, что стабильные зародыши новой фазы возникают в результате тепловых флуктуаций упорядоченной структуры. Переохлажденная жидкость является метастабильной по отношению к возникновению в ней центров кристаллизации. В данном случае метастабильность означает наличие энергетического барьера, который можно определить следующим образом.
Движущей силой фазового превращения является разность свободных энергий системы в ее конечном и начальном состояниях. Однако при образовании малых частиц новой фазы свободная энергия в первый момент возрастает, что обусловлено тем, что значительная часть атомов новой фазы расположена в переходной области между фазами, т.е. на границе раздела фаз. Полагая, что малый зародыш, состоящий всего из нескольких атомов, рассматривается как макроскопическая частица (которая характеризуется соответствующими параметрами), а переходная область между жидкостью и кристаллом описывается как некоторая геометрическая поверхность, можно предложить выражение для приращения свободной энергии при образовании кристаллического зародыша в жидкой фазе как сумму двух слагаемых – изменения объемной составляющей и члена, обусловленного возникновением поверхности раздела фаз:
|
|
|
ΔG  . r3.
. r3.  + 4πr2σ, (4)
+ 4πr2σ, (4)
где r – радиус центра кристаллизации, 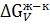 - изменение свободной энергии при переходе жидкость-кристалл (в расчете на единицу объема), σ -поверхностное натяжение на границе жидкость-кристалл.
- изменение свободной энергии при переходе жидкость-кристалл (в расчете на единицу объема), σ -поверхностное натяжение на границе жидкость-кристалл.
Были предприняты неоднократные попытки построения точных теорий, исключающих указанные приближения. Однако при этом обычно рассчитанные параметры неудовлетворительно согласуются с полученными экспериментально. Представленные же выше допущения классической теории зарождения кристаллической фазы позволяют сравнивать результаты расчета с экспериментом.
При малых значениях r второе слагаемое в уравнении (4) растет быстрее, чем уменьшается первое (для переохлажденной жидкости приращение свободной энергии  <0). Поэтому зависимость ΔG =ƒ(r) проходит через максимум (рис.4).
<0). Поэтому зависимость ΔG =ƒ(r) проходит через максимум (рис.4).
Рис.4. Зависимость изменения свободной энергии образования центра кристаллизации от его размера (а) и температурная зависимость скорости образования зародышей (б).
Соответствующий размер критического зародыша (r*) можно найти из условия (dΔG/dr)=0
r* =  (5)
(5)
Величина энергетического барьера (ΔG*) может быть найдена путем подстановки (5) в (4):
ΔG* = 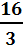 .
.  . (6)
. (6)
Вероятность того, что в результате флуктуации в переохлажденной жидкости возник зародыш критического размера, определяется уравнением
|
|
|
p = exp  .
.
Если в единице объема содержится N частиц, то число центров кристаллизации критического размера Nr в том же объеме переохлажденной жидкости будет
Nr = N. exp  .
.
Центр кристаллизации критического размера с равной вероятностью может как раствориться, так вырасти. Если к подобному центру кристаллизации присоединяются другие частицы, то он становится центром роста новой фазы; при этом скорость присоединения будет пропорциональна количеству мест на поверхности критического зародыша (Ns).
Частота переходов частиц (ν) через барьер на границе жидкость-зародыш равна
ν =  exp
exp 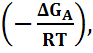
где h – постоянная Планка, ΔGA – энергия активации процесса перехода частиц из одной фазы в другую. Соответственно скорость зародышеобразования (I) можно представить как произведение двух сомножителей:
I = Ns.  exp
exp  . N. exp
. N. exp  (7)
(7)
В этом уравнении первый экспоненциальный сомножитель характеризует скорость перехода частиц из жидкой фазы в твердую кристаллическую. Величину ΔGА можно отождествить с энергией активации диффузии. Эту величину принято называть кинетическим барьером зародышеобразования.
Второй экспоненциальный сомножитель характеризует вероятность возникновения критического зародыша, которая определяется высотой энергетического барьера ΔG*. Наличие этого барьера обусловлено тем, что образование новой фазы малого размера из-за преобладающего вклада поверхностной энергии является невыгодным. В соответствии с его природой, ΔG* называют термодинамическим барьером образования зародышей.
Из уравнения (6) следует, что величина термодинамического барьера ΔG* зависит от температуры.
При температуре плавления Тпл свободная энергия жидкости и кристалла одинаковы, т.е.
 = ΔHV - Тпл ΔSV = 0, (8)
= ΔHV - Тпл ΔSV = 0, (8)
где ΔHV, ΔSV энтальпия и энтропия плавления единицы объема кристалла соответственно. Из уравнения (8) следует
ΔSV = 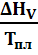 .
.
Обычно, температурным изменением энтальпии и энтропии плавления пренебрегают, но для относительно точных расчетов температурную зависимость ΔHV и ΔSV можно оценить, используя закон Кирхгофа для теплового эффекта химической реакции. В простейшем случае при любой температуре Т < Тпл имеет место следующее соотношение:
|
|
|
 = ΔHV - Тпл ΔSV = ΔHV .
= ΔHV - Тпл ΔSV = ΔHV . 
или
 =
=  , (9)
, (9)
и, с учетом (6),
ΔG* = 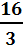 .
. 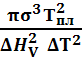 , (10)
, (10)
где ΔТ – переохлаждение жидкости относительно температуры плавления.
Из уравнения (10) следует, что высота термодинамического барьера обратно пропорциональна квадрату переохлаждения жидкости ΔТ. Иными словами, кристаллическое состояние по сравнению с жидким при понижении температуры становится все более и более выгодным.
Представленный выше вывод выражения для скорости образования зародышей кристаллической фазы является упрощенным. В частности, не нашел отражения факт возможного растворения (но не роста) возникших в жидкости центров кристаллизации, т.е. наряду с прямым возможен и обратный процесс. Возможная вероятность растворения зародыша кристаллической фазы достигшего критического размера учитывается при помощи параметра Z, который называется множителем Зельдовича. Таким образом,
I = Z.  Ns . N. exp
Ns . N. exp  . (11)
. (11)
Величину кинетического барьера образования зародышей разумно приравнять к свободной энергии активации вязкого течения, которая согласно уравнению Стокса-Эйнштейна равна энергии активации диффузии. Действительно, присоединение частиц жидкости к поверхности растущего зародыша происходит в результате термически активированного перемещения, по сути, подобного перемещению той же частицы при вязком течении или в процессе диффузии. В этой связи ΔGА либо практически не зависит от температуры (если энтропию активации принять равной нулю), либо растет с понижением температуры. Таким образом, скорость образования зародышей (I) с температурой меняется следующим образом: при температуре плавления величина термодинамического барьера бесконечна и скорость образования зародышей равна нулю. С понижением температуры высота термодинамического барьера уменьшается и скорость зародышеобразования возрастает. Однако параллельно с этим растет вязкость жидкости и это ограничивает рост до бесконечности величины скорости зародышеобразования. При дальнейшем понижении температуры уменьшается вероятность преодоления кинетического барьера, что приводит к снижению скорости образования зародышей. Таким образом, температурная зависимость скорости образования зародышей будет проходить через максимум.
|
|
|
Анализ уравнения (11) и экспериментальные данные говорят о том, что температура ТI, при которой скорость образования зародышей максимальна, близка для стеклообразующих жидкостей к температуре стеклования Тg.
Величина максимальной скорости образования зародышей зависит как от термодинамических характеристик вещества, так и от высоты кинетического барьера. Чем выше вязкость метастабильной жидкости, тем меньше максимальная скорость образования зародышей. Для стеклообразующих систем экспериментально иногда удается получить только восходящую ветвь зависимости I = ƒ(Т) (рис.4), так как в твердом стекле флуктуации упорядоченности невозможны, и, как следствие, не могут возникать и центры кристаллизации.
Если жидкость резко охладить и перевести из стабильного состояния в состояние метастабильной жидкости, а затем оценить зависимость скорости образования центров кристаллизации от времени, то оказывается, что число центров кристаллизации становится заметной величиной только по прошествии некоторого времени τ. Это время релаксациизародышеобразования. Порядок величины τ дается соотношением
τ =  ,
,
где nk – число атомов в критическом зародыше, D – коэффициент диффузии. Характерный вид получаемых экспериментальных зависимостей представлен на рис.5. Различают стационарное (скорость образования зародышей не зависит от времени I ≠ ƒ(Т)) и нестационарное зародышеобразование. Временная зависимость скорости нестационарного зародышеобразования подчиняется экспоненциальной зависимости
I = Io exp (-  ), (12)
), (12)
где Io – стационарная скорость образования зародышей, которая описывается уравнением (11).
Рис.5. Зависимость количества центров кристаллизации от времени изотермической выдержки.
Если переохладить жидкость от температуры, равной температуре плавления (Т = Тпл), до температуры Т (Т< Тg), причем этот интервал необходимо пройти с такой скоростью q, чтобы в единице объема вещества возник всего один центр кристаллизации (Nk=1), то поскольку такое количество кристаллической фазы в объеме аморфной экспериментально не определяется, считается, что материал не содержит кристаллических включений и будет считаться стеклообразным. Если при этом считать, что в процессе охлаждения температура меняется линейно и
Т = Тпл – qt,
из уравнения (12) следует, что
dN = Io. exp  dt.
dt.
При замене переменных, получается
N =  . exp
. exp 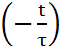 dt = -
dt = -  . (13)
. (13)
|
|
|
Если выражение (13) приравнять к единице, можно найти скорость охлаждения qкр – скорость, при которой в единице объема возникает только один кристаллический зародыш. Это означает, что если вещество охлаждать со скоростью q >qкр, то в процессе охлаждения не возникнет ни один центр кристаллизации, следовательно, получится вещество в стеклообразном состоянии.
С учетом сделанных приближений, уравнение (13) справедливо для случая гомогенного образования центров кристаллизации. Возможен однако случай гетерогенного образования кристаллов: при этом одна из сторон зародыша критического размера находится в контакте с твердой фазой, поэтому наряду с поверхностью раздела жидкость – зародыш возникает еще и поверхность раздела кристалл – зародыш. Если поверхностное натяжение на границе раздела кристалл-зародыш значительно меньше поверхностного натяжения на границе жидкость-зародыш (σкр-зар << σж-зар) то при одинаковых переохлаждениях свободная энергия образования зародыша на твердой поверхности меньше, чем в объеме расплава. Это означает, что максимум скорости образования центров кристаллизации должен сместиться в сторону более высоких температур.
|
|
|


