 |
Скорость роста кристаллов.
|
|
|
|
Считается, что размер центров кристаллизации - зародышей - лежит в пределах от 1 до 100 нм. Пусть по мере роста зародыша его размеры линейно изменяются со временем согласно выражению
r = r* + ut
где u – скорость роста, r* - критический радиус зародыша. Если r >> r*, то в дальнейшем радиусом критического зародыша можно пренебречь. Объем кристаллического включения сферической формы можно вычислить так:
V = 
πr3 = π(r* + ut)3 ≈ πu3t3.
Изменение свободной энергии частицы, находящейся в жидкости, при присоединении к поверхности растущего кристалла можно представить в виде зависимости от обобщенной координаты реакции, характеризующей расстояние от границы раздела фаз (рис.6).
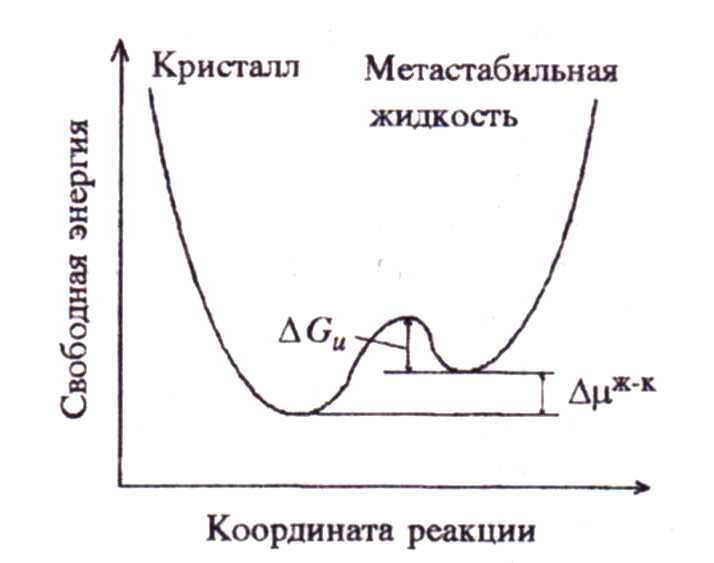
Рис.6. Зависимость свободной энергии частицы от ее положения относительно границы раздела фаз.
Тогда выражение для частоты перехода частицы из жидкости в растущий кристалл
νж-к = ν . exp 
,
где ν – частота колебаний частиц.
Растворение кристалла – частоту перехода частиц из кристалла в жидкость можно определить по уравнению
νк-ж = ν . exp 
,
где μж-к – изменение свободной энергии при переходе моля частиц из жидкого состояния в твердое (кристаллическую фазу). В предположении, что ΔHпл и ΔSпл слабо зависят от температуры,
Δμж-к =ΔHпл – TΔSпл = Δ 
. (14)
Количество частиц, присоединившихся к растущему кристаллу за единицу времени – результирующая частота перехода частиц (Δν), будет равно
Δν = νж-к + νк-ж = ν . exp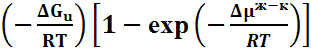 
.
Тогда выражение для скорости роста кристаллов можно описать следующим уравнением:
u = a .Δν = a . ν . exp 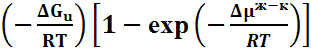, (15)
где а – размер присоединяющейся частицы.
При выводе уравнения (15) предполагается, что имеется резкая ступень роста. Кристалл растет (т.е. эта ступень перемещается) в результате двух последовательных процессов: диффузионных переходов частиц жидкости к поверхности раздела фаз (1) и присоединения частиц к ступени роста (2). При таком механизме роста граница раздела фаз непрерывно перемещается перпендикулярно плоскости роста: это так называемый нормальный рост. Если рост происходит путем присоединения частиц к поверхностной спирали винтовых дислокаций, в выражении для скорости роста появляется сомножитель ƒ, отражающий то обстоятельство, что растет не вся поверхность, а только место выхода дислокации:
|
|
|
u = a.ƒ. ν . exp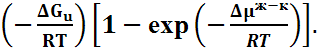 
(16)
Из уравнения (16) следует, что температурная зависимость скорости роста центров кристаллизации имеет такой же характер, как и зависимость
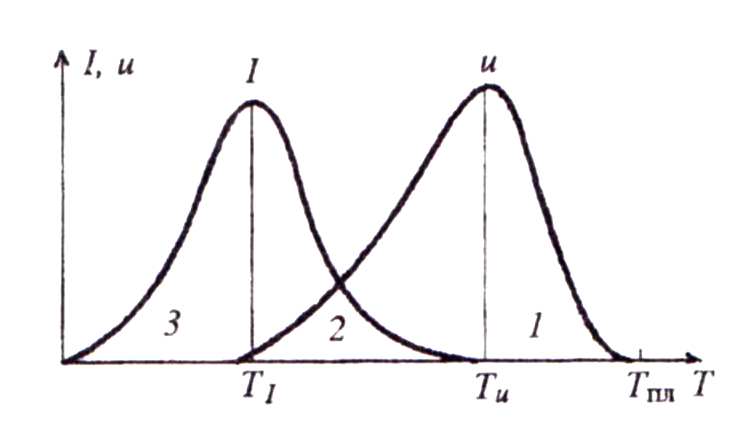
Рис.7. Температурная зависимость скорости образования зародышей (I) и скорости роста кристаллов (U).
скорости образования зародышей. При этом максимум скорости роста по отношению к максимуму скорости зародышеобразования сдвинут в сторону более высоких температур (рис.7).
На этих зависимостях можно выделить следующие области:
1. Область температур, где скорость образования центров кристаллизации равна нулю, а скорость роста кристалла отлична от нуля и имеет какое-то заметное значение (область 1). В этой области можно наблюдать стабильное переохлажденное состояние жидкости; именно в этом интервале температур выращивают монокристаллы на затравках.
2. Область температур, в которой зависимости скорости роста зародышей и скорости роста кристаллов перекрываются (область 2). В этой области температур создаются наиболее благоприятные условия для кристаллизации вещества.
3. Область температур, в которой скорость образования зародышей велика, а скорость роста кристаллов практически равна нулю (область 3). Этот температурный интервал может быть использован (путем термической обработки расплава) для создания большого числа центров кристаллизации; возникающие при этом центры кристаллизации (центры образования зародышей) могут быть выявлены термообработкой при более высокой температуре в той области температур, в которой значение скорости роста кристаллов относительно высока.
|
|
|
Если рассматривать процесс охлаждения стеклообразующей жидкости до получения из нее вещества в стеклообразном состоянии, а затем процесс нагревания полученного таким образом стекла, то можно выявить следующие закономерности. В процессе охлаждения в области температур вблизи температуры плавления (Тпл) создаются благоприятные условия для роста кристаллов, однако, поскольку центров кристаллизации в объеме метастабильной жидкости еще не образовалось, расти по существу нечему. При дальнейшем снижении температуры в объеме жидкости можно создать большое количество центров кристаллизации, но до значительных размеров они вырасти уже не смогут, т.к. в этом температурном интервале значения скорости роста уже невелики. Такая последовательность процессов благоприятствует процессам стеклообразования. При нагревании твердого стекла процесс кристаллизации его происходит в «нормальной» последовательности: сначала появляются центры кристаллизации (в том числе проявляются и те, которые образовались при охлаждении жидкости), а затем, при более высоких температурах, у них появляется возможность вырасти до заметных размеров.
Общая скорость кристаллизации.
Абсолютные величины скорости образования зародышей (центров кристаллизации) и скорости роста кристаллов экспериментально определить сложно, а зачастую, особенно при решении прикладных задач, в этом нет необходимости. Во многих случаях достаточно знать, как от времени термической обработки (термической истории) будет зависеть объемная доля кристаллической фазы в стеклообразном образце. Считается, что наличие в стекле объемной доли кристаллической фазы менее 10-4% не обнаруживается ни одним из существующих в настоящий момент методом исследования структуры стекла (возможно, кроме измерения оптических потерь в волокнах из сверхчистых стекол). Поэтому указанная величина может быть принята за абсолютный критерий стеклообразования.
|
|
|
Представляет интерес проследить изменение объемной доли кристаллической фазы в образце при изотермической выдержке, в случае, когда температура термообработки такова, что скорость образования зародышей и скорость роста кристаллической фазы имеют конечные величины.
Пусть объем системы равен Vo, причем в начальный момент времени кристаллическая фаза в образце отсутствует. Количество центров кристаллизации, возникающих за период времени от τ до τ + dτ, равно
dN = Vo. I.dτ,
где I – скорость образование центров кристаллизации, т.е. количество зародышей, возникающих в единицу времени в единице объема.
В дальнейшем эти центры кристаллизации растут со скоростью u и объем одного растущего зародыша равен
d 
= π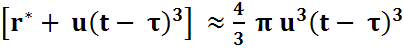 
.
Изменение объема кристаллической фазы, связанное с возникающими и растущими центрами кристаллизации, можно вычислить следующим образом:
. (17)
Если I и u не зависят от времени, т.е. устанавливается стационарный режим, тогда
= 
.
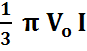
Рассмотрим два предельных случая.
1. Vкр << Vo, т.е. закристаллизовалась малая часть объема системы. Тогда доля закристаллизованного объема (α) представляется как
α =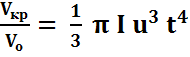 
. (18)
2. Vкр ≈ Vo. С течением времени доля закристаллизованного объема увеличивается. В этом случае образование новых центров кристаллизации возможно только в той части системы, которая не закристаллизовалась. Объем этой части системы Vo - Vкр. Тогда количество вновь образующихся зародышей определяется как
dN = I (Vo - Vкр)dτ,
а уравнение (17) можно записать в следующем виде:
.
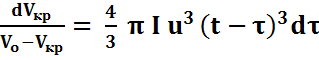После разделения переменных и интегрирования получаем
α = 1 – exp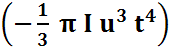 
или
α = 1 – exp 
. (19)
Уравнение (19) называется уравнением Колмогорова – Аврами. Оно позволяет на основании значений I и u рассчитать степень превращения стекла или переохлажденной жидкости в кристаллическое состояние.
Тем не менее, анализ значительного количества экспериментальных данных указывает на то, что зависимость доли закристаллизованного объема от времени в условиях изотермической выдержки описать уравнением (19) не удается. Обычно для этого применяется уравнение, обобщенный вид которого можно проедставить как
|
|
|
α = 1 – exp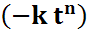 
.,
где 1 ≤ n ≤ 4, причем может принимать и нецелочисленные значения. Такое расхождение теории с экспериментом объясняется снятием ограничесний, наложенных при выводе уравнения (19).
Первое ограничение состоит в том, что кристал может расти с одинаковой скоростью во всех трех измерениях. Однако в реальных условиях скорость роста кристаллов в различных направлениях различна, поэтому вводится понятие мерности роста. При гомогенном зародышеобразования и трехмерном росте величина n изменяется в пределах от 3 до 4. В случае двумерного роста значение n изменяется в пределах 2 < n <3, так как объем кристаллической фазы пропорционален квадрату размера зародыша. Соответственно, при одномерном росте и гомогенном зародышеобразовани
1 < n < 2.
Второе ограничение при выводе уравнения (19) это гомогенное зародышеобразование. в реальной системе может происходить образование зародышей на постороннох примесях. Это означает, что число мест N, на которых возможно образование зародышей, фиксировано. В начальный момент времени изотермической выдержки образование зародышей происходит со скоростью, соответствующей скорости гетерогенного зародышеобразования, а затем, когда места для возникновения зародышей исчерпаны, падает до нуля. В конечном итоге это снижает показатель степени в уравнении Колмгорова – Аврами на единицу.
|
|
|
