 |
Задачи репродуктивного уровня
|
|
|
|
Тесты для проверки остаточных знаний.
Задания под пунктом а) для первого варианта, под пунктом б) -для второго варианта
ПРИМЕРЫ ТЕСТОВЫХ ЗАДАНИЙ
Задания приводятся в той форме, которую студенты видят на экране компьютера во время проведения тестирования. Слева от вертикальной черты расположены условия заданий, справа — варианты ответа. Правильный вариант (или варианты) ответа отмечен точкой. Некоторые тестовые задания требуют от студента ввести ответ или расставить соответствия между математическими объектами, стоящими справа и слева от вертикальной черты.
Задание 1.

 Укажите график периодической функции.
Укажите график периодической функции.
Задание 2.
Дана функция
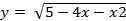 + lg (x+3)
+ lg (x+3)
Тогда ее областью определения является.
Задание 3
По формулам Крамера решить систему:
а) 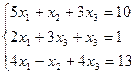
 а) (1;-1;2) б)(3:-3:5) в)(-1;2;4)
а) (1;-1;2) б)(3:-3:5) в)(-1;2;4)
б) 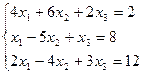
 а) (1;-1;2) б)(-3:-3:1) в)(-1;2;4)
а) (1;-1;2) б)(-3:-3:1) в)(-1;2;4)
Задание 4
Методом Гаусса решить систему:
а) 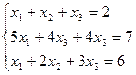
 а) (-1;2;1) б)(3:-3:5) в)(-1;2;4)
а) (-1;2;1) б)(3:-3:5) в)(-1;2;4)
б) 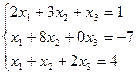
 а) (1;-1;2) б)(-3:-3:1) в)(-1;2;4)
а) (1;-1;2) б)(-3:-3:1) в)(-1;2;4)
Задание 5.
а) Если 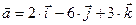 , то
, то 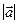 =…
=…
1) 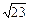 ; 2)7; 3) –1; 4)
; 2)7; 3) –1; 4)  .
.
б)Если 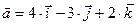 , то
, то 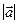 =…
=…
1)  ; 2)3; 3) –4; 4)
; 2)3; 3) –4; 4)  .
.
Задание 6
а) Даны векторы 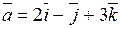
 ,
,
Их скалярное произведение 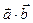 равно: 1)
равно: 1) 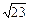 ;2)7; 3) 11; 4)
;2)7; 3) 11; 4)  .
.
в) 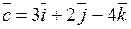

Их скалярное произведение 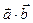 равно: 1)
равно: 1) 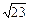 ; 2)7; 3) –11; 4)
; 2)7; 3) –11; 4)  .
.
Задание 7
а) В треугольнике с вершинами 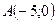 ,
, 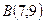 ,
, 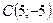
длина высоты, опущенной из вершины С на сторону АВ составит:
в) В треугольнике с вершинами 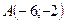 ,
, 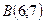 ,
, 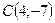
длина высоты, опущенной из вершины С на сторону АВ составит:
Задание 8
Предел функции равен:
а) 1. 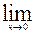
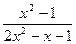 б) 1.
б) 1. 
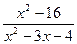
2. 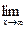
 2.
2. 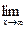
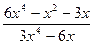
А)в) 1. 1) 2; 2) 1/4; 3) 8/5; 4)0.5
2. 1)4; 2) 2; 3) -3 4) 0
Задание 9
Точками экстремума функций
а) y=x  являются: а) -1; 2 б) 3; 1 в) -3; 2
являются: а) -1; 2 б) 3; 1 в) -3; 2
б)y=x 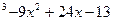 являются: а) 4; 2 б) 3: -3 в) 1; 2
являются: а) 4; 2 б) 3: -3 в) 1; 2
|
|
|
Задание 10
а) Угловой коэффициент прямой 6 x + 2 y – 5 = 0 равен …
1) 3 2) −6 3) 2 4) −3.
в) Угловой коэффициент прямой 6 x + 3 y – 2 = 0 равен …
1) 3 2) −6 3) -2 4) −3.
) Задание 11
а) Координата x 0 точки А (х 0; 1; 7), принадлежащей плоскости 5 x + y – z + 1 = 0, равна …
1) 4; 2) 1; 3) 3; 4) 2.
б) Координата x 0 точки А (х 0; 1; 7), принадлежащей плоскости 3 x - y +3 z + 1 = 0, равна …
1) 4; 2) -7; 3) 3; 4) 2.
) Задание 12
а)Производная функции  имеет вид …
имеет вид …
1) 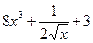 ; 2)
; 2) 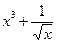 ; 3)
; 3) 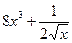 ; 4)
; 4) 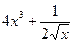 .
.
. б) Производная произведения xex равна …
1) 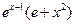 ; 2)
; 2) 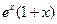 ; 3)
; 3) 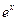 ; 4)
; 4) 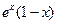 .
.
) Задание 13
а) В урне 4 белых и 6 черных шаров. Из урны вынимают сразу 2 шара.
Вероятность того, что шары разного цвета, равна...
1) 8/15; 2) 1; 3) 3/5; 4) 1/24.
,
б) Два стрелка производят по одному выстрелу. Вероятности попадания в цель для первого и ВТО рого стрелков равны 0,6 и 0,3 соответственно. Тогда вероятность того, что в цель попадут оба стрелка, равна…
1) 0,28; 2) 0,15; 3) 0,9; 4) 0,18.
) Задание 14
Вычислить площадь фигуры, ограниченной линиями:
а) 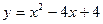
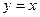
б) 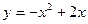
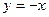
) Задание 15
Вычислить а ) 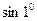 б)
б) 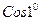 и оценить погрешность вычисления
и оценить погрешность вычисления
) Задание 16
Решить дифференциальное уравнение при 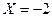
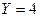
а) 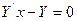
б) 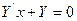
Критерии оценки:
- оценка «отлично» выставляется студенту, если выполнено верно 90% работы;
- оценка «хорошо», если выполнено 70% работы;
- оценка «удовлетворительно», если выполнено 50% работы;
- оценка «неудовлетворительно», если выполнено менее 50% работы;
- оценка «зачтено» выставляется студенту, если выполнено более 50% работы;
- оценка «не зачтено» если выполнено менее 50% работы.
Варианты индивидуальных заданий.
Комплект задач по теме: Матрицы.
(2 варианта под а)первый вариант б) второй вариант)
1. Найдите матрицу С-1, обратную к матрице С = АВ’ + 3Е:
а) А =  В=
В= 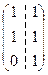 в) А =
в) А =  В=
В= 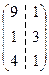
2. Определить максимальное число линейно независимых строк матрицы:
а) 

1 3 1 4 1
11 3 5 5 2
5 5 3 17 12
4 2 2 3 1
б)
 |  |
-5 1 5 2 1
6 -2 -10 -4 1
7 1 5 2 -8
|
|
|
3. Решить матричные уравнения:
а) 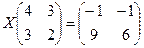
б) 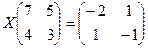
4. Привести к
диагональному виду матрицу А.
А= 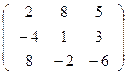
А= 
Критерии оценки:
- оценка «отлично» выставляется студенту, если студентом выполнены верно 4 задания;
- оценка «хорошо» студентом выполнены первые четыре верно или выполнено 4-е и три других;
- оценка «удовлетворительно» выставляется студенту, если студентом выполнены верно три любых задания; продемонстрирована знание материала на уровне воспроизведения, умение решать задачи по рассматриваемым темам с помощью конспекта;
- оценка «неудовлетворительно» студент не владеет материалом, пользоваться вспомогательным конспектом не умеет.
Задачи для письменного опроса.
Комплект задач
по теме: Теория вероятностей и математическая статистика.
Задачи репродуктивного уровня
1 В урне 16 шаров: 5 белых, 7 черных и 4 красных. Из урны 4 раза вынимают по одному шару, возвращая каждый раз в урну. Найти вероятность того, что первый шар будет белым, второй - черным, а третий и четвертый - красными.
2. В лаборатории имеется 15 автоматических машин и 10 полуавтоматов. Вероятность того, что за время выполнения некоторого задания автомат не выйдет из строя, равна 0,95. Для полуавтомата эта вероятность равна 0,85. Студент выполняет задание на машине, выбранной наудачу. Найти вероятность того, что до конца выполнения задания машина не выйдет из строя.
3. Определить вероятность того, что в семье, имеющей пять детей, будет три девочки и два мальчика. Вероятности рождения мальчика и девочки предполагаются одинаковыми.
4. Найти вероятность того, что событие А наступит ровно 1850 раз в 2500 испытаниях, если вероятность появления этого события в каждом испытании равна 0,75.
5.Закон распределения дискретной случайной величины
Найти математи ческое ожидание и дисперсию.
| X | -4 | -3 | -2 | ||
| р | 0,1 | 0,1 | 0,5 | 0,2 | 0,1 |
|
|
|


