 |
Расчет статических стержневых систем
|
|
|
|
Курсовая работа
Тема: Процедура расчета и создания стержней с заданными характеристиками
Содержание
1 Основные аспекты создания стержней
1.1 Растяжение в центре и по бокам
1.2 Расчет статических стержневых систем
1.3 Расчет основных переменных
2 Оценка параметров закручивания
3 Процедура создания стержней
3.1 Создание стальной балки
3.2 Выбор материала
3.3 Создание стержня определенной жесткости
Основные аспекты создания стержней
Растяжение в центре и по бокам
Для заданного ступенчатого стержня (рис. 1,а) при осевых нагрузках F1=a1qa, F2=a2qa требуется:
1. Определить реактивную осевую силу в опорном сечении.
2. Определить продольные силы Nz, нормальные напряжения sz и перемещения w в характерных точках и построить их эпюры.
3. Определить опасное сечение и подобрать необходимую площадь A стержня из условия прочности на растяжение или сжатие.
Принять: α1=3, α2=4, а=1 м, q=600 кН/м, [σр]=160 МПа, [σс]=60МПа
Решение
1. Определение опорной реакции.
Составляем уравнение равновесия в проекции на ось z:
ΣZi=0
RB - qa + 4qa + q2a + 3qa = 0
RB = qa + 4qa - q2a - 3qa = 0
2. Построение эпюр продольных сил, напряжений и перемещений.
Эпюра Nz. Строится по формуле:
N = N ± qz
Знак «плюс» соответствует погонной нагрузке, вызывающей растяжение бруса, а знак «минус» берется в случае сжатия. В сечениях где приложены сосредоточенные силы (сеч. C и E), на эпюре Nz имеют место скачки. Если сосредоточенная сила вызывает растяжение, то скачок вверх (сеч. E), в случае сжатия – скачок вниз (сеч. С). На участках BC и CD продольная сила изменяется по линейному закону (qz¹0), а на участке DE продольная сила постоянна (qz=0). Вычисляем значения продольной силы в характерных точках и строим эпюру Nz (рис. 1,б)
|
|
|
NE = 3qa
NED = NDE = 3qa
NDC = NDE + q2a = 3qa + q2a = 5qa
NC = NDC – 4qa = 5qa – 4qa = qa
NB = NC – qa = qa – qa = 0
Эпюра σz. Напряжение в поперечных сечениях связаны с продольной силой соотношением
σz = 
Учитывая, что брус имеет ступенчато – переменное сочетание, характер распределения нормальных напряжений по длине бруса остается таким же как для продольной силы. Однако в местах резкого изменения формы бруса (сеч. C и D) на эпюре σz, в отличие от Nz, возникают скачки, связанные с изменением площади поперечного сечения. Вычисляем напряжения в характерных точках и строим эпюру σz (рис. 1,в)
σE = 
σDE = σE = 
σD = 
σCD = 
σC = 
Эпюра w. Она строится по формуле
w(z) = w0 + 
где w0 - перемещение в начале участка;
wz - площадь эпюры σz от начала участка до рассматриваемого сечения.
При отсутствие погонной нагрузки (уч. DE) напряжения постоянны, а перемещения изменяются по линейному закону. На участках с погонной нагрузкой напряжения изменяютяс по линейному закону, а перемещения – по квадратичному (уч. BC и CD). Вычисляем перемещения в характерных точках и сторим эпюру w (рис. 1,г)
wB = 0
wC = wB + 
wD = wC + 
wE = wD + 
Подбор сечений.
Из условия прочности на растяжение
σmax £ [σр]
 £ [σр]
£ [σр]
Aр ³  см2
см2
Площадь сечения работающего на сжатие Ac = 0, т.к. σmin =0. Окончательно принимаем A=Aр=187,5 см2.
Исходя из найденной площади сечения, определим полное удлинение ступенчатого бруса
Dl=wE=  м =1,5 мм
м =1,5 мм
Расчет статических стержневых систем
Для заданной стержневой системы (рис. 2, а) требуется:
1. Определить усилия в стержнях и подобрать их сечения из двух равнобоких уголков по методу допускаемых напряжений, обеспечив заданное соотношение площадей A2/A1=1,6. Допускаемое напряжение принять равным [σ] = 160 МПа.
2. При принятых размерах сечений стержней определить грузоподъемность конструкции по методу допускаемых нагрузок.
|
|
|
3 Оценить в процентах дополнительный резерв грузоподъемности, получаемый при переходе от метода допускаемых напряжений к методу допускаемых нагрузок.
Принять: F=500 кН
Решение
1. Определение усилий в стержнях.
Данная система является однажды статически неопределимой (4 неизвестных при 3 уравнениях статики), поэтому в дополнение к уравнениям статики необходимо составить одно уравнение совместности деформаций.
Уравнение статики
Σm0=0
N1·2a·cos45° + N2·4a·cos30° - 3a·F = 0
N1  + N2 2
+ N2 2  =3F
=3F
Уравнение совместности деформаций. Из подобия треугольников ABB1 и BCC1 имеем:



Заменяя по закону Гука деформации через усилия и подставляя в последние уравнение, получим

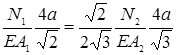
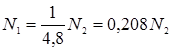
Решая совместно уравнения (1) и (2), находим усилия в стержнях




2. Подбор сечений стержней.
Следует заметить, что подобранные сечения должны одновременно удовлетворять и условию прочности, и заданному соотношению площадей. Чтобы удовлетворить обоим названым условиям, сопоставим два варианта.
По первому варианту сечение 1-го стержня подберем из условия прочности, а 2-го – исходя из заданного соотношения площадей, т.е.
 см2
см2
 см2
см2
По второму варианту из условия прочности находится сечение 2-го стержня, а из заданного соотношения – сечение 1-го
 см2
см2
 см2
см2
Окончательно принимаем второй вариант, так как он обеспечивает и прочность обоих стержней, и заданное соотношение площадей. По таблице сортамента для равнополочных уголков в соответствие с ГОСТ 8509-86 принимаем:
для 1-го стержня – 2 уголка 70´70´6 (А1=2·8,15=16,3 см2)
для 2-го стержня – 2 уголка 90´90´7 (А2=2·12,3=24,6 см2)
3. Определение грузоподъемности конструкции по методу допускаемых нагрузок.
Составляем уравнения предельного равновесия.


 кН
кН
Следовательно, при переходе от одного метода допускаемых напряжений к методу допускаемых нагрузок можно повысить грузоподъемность конструкции в
 раза или на 16 %
раза или на 16 %
|
|
|


