 |
Алгоритмы линейной структуры
|
|
|
|
Понятие алгоритма
Алгоритм - четкое описание последовательности действий, которые необходимо выполнить при решении задачи. Можно сказать, что алгоритм описывает процесс преобразования исходных данных в результаты, т.к. для решения любой задачи необходимо:
1. Ввести исходные данные.
2. Преобразовать исходные данные в результаты (выходные данные).
3. Вывести результаты.
Разработка алгоритма решения задачи - это разбиение задачи на последовательно выполняемые этапы, причем результаты выполнения предыдущих этапов могут использоваться при выполнении последующих. При этом должны быть четко указаны как содержание каждого этапа, так и порядок выполнения этапов. Отдельный этап алгоритма представляет собой либо другую, более простую задачу, алгоритм решения которой известен (разработан заранее), либо должен быть достаточно простым и понятным без пояснений. Разработанный алгоритм можно записать несколькими способами:
- на естественном языке;
- в виде блок-схемы;
- в виде R-схемы.
Рассмотрим пример алгоритма на естественном языке:
1. Ввести в компьютер числовые значения переменных а, b и с.
2. Вычислить d по формуле d = b2 - 4ас.
3. Если d < 0, то напечатать сообщение "Корней нет" и перейти к п.4. Иначе вычислить и напечатать значения x1 и x2.
4. Прекратить вычисления.
Изображение алгоритма в виде блок-схемы
Блок-схемой называется наглядное графическое изображение алгоритма, когда отдельные его этапы изображаются при помощи различных геометрических фигур - блоков, а связи между этапами (последовательность выполнения этапов) указываются при помощи стрелок, соединяющих эти фигуры. Блоки сопровождаются надписями. Типичные действия алгоритма изображаются следующими геометрическими фигурами:
Блок начала-конца алгоритма (рис. 1.1). Надпись на блоке: "начало" ("конец").
Блок ввода-вывода данных (рис. 1.2). Надпись на блоке: слово "ввод" ("вывод" или "печать") и список вводимых (выводимых) переменных.
|
|
|

| 
|
| Рис. 1.1. Блок начала-конца алгоритма | Рис. 1.2. Блок ввода-вывода данных |
Блок решения или арифметический (рис. 1.3). Надпись на блоке: операция или группа операций.
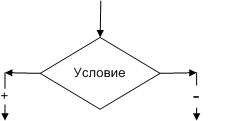
Условный блок (рис. 1.4). Надпись на блоке: условие. В результате проверки условия осуществляется выбор одного из возможных путей (ветвей) вычислительного процесса. Если условие выполняется, то следующим выполняется этап по ветви "+", если условие не выполняется, то выполняется этап по ветви "–".

| 
|
| Рис. 1.3. Арифметический блок | Рис. 1.4. Условный блок |
В качестве примера рассмотрим блок-схему алгоритма решения уравнения (рис. 1.5), описанного в предыдущем подразделе.

|
| Рис. 1.5. Блок-схема алгоритма решения квадратного уравнения |
Алгоритмы линейной структуры
Линейный алгоритм - это такой, в котором все операции выполняются последовательно одна за другой (рис. 1.6).

|
| Рис. 1.6 Размещение блоков в линейном алгоритме |
Рассмотрим несколько примеров линейных алгоритмов.
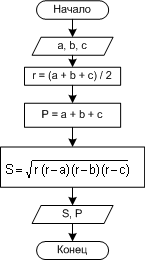
ПРИМЕР 1.1. Зная длины трех сторон треугольника, вычислить площадь и периметр треугольника.
Пусть a, b, c - длины сторон треугольника. Необходимо найти S - площадь треугольника, P - периметр.
| Для нахождения площади можно воспользоваться формулой Герона: | 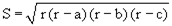
| где r - полупериметр. |
Входные данные: a, b, c.
Выходные данные: S, P.
Блок-схема алгоритма представлена на рис. 1.7.
|
| Рис. 1.7. Алгоритм примера 1.1 |
Внимание!!! В этих блоках знак "=" означает не математическое равенство, а операцию присваивания. Переменной, стоящей слева от оператора, присваивается значение, указанное справа. Причем это значение может быть уже определено или его необходимо вычислить с помощью выражения. Например, операция r = (a+b+c)/2 - имеет смысл (переменной r присвоить значение r=(a+b+c)/2), а выражение (a+b+c)/2=r - бессмыслица.
|
|
|
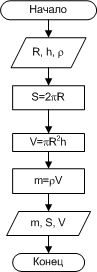
ПРИМЕР 1.2. Известны плотность и геометрические размеры цилиндрического слитка, полученного в металлургической лаборатории. Найти объем, массу и площадь основания слитка.
Входные данные: R - радиус основания цилиндра, h - высота цилиндра, ρ- плотность материала слитка.
Выходные данные: m - масса слитка, V - объем, S - площадь основания.
Блок-схема представлена на рис. 1.8.
|
| Рис. 1.8. Алгоритм примера 1.2 |
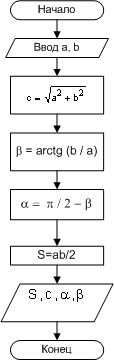
ПРИМЕР 1.3. Заданы длины двух катетов в прямоугольном треугольнике. Найти длину гипотенузы, площадь треугольника и величину его углов.
Входные данные: a, b - длины катетов.
Выходные данные: с - длина гипотенузы, S - площадь треугольника, α, β - углы.
Блок-схема представлена на рис.1.9.
|
| Рис. 1.9 Алгоритм примера 1.3 |
|
|
|


