 |
Классический метод для действительных корней.
|
|
|
|
В докоммутационном режиме источник питания был отключен, поэтому токи и напряжения схемы были равны нулю, следовательно, независимые начальные условия:
iL (0+) = iL (0-) = 0, uC (0+) = uC (0-) = 0. (3.1)
Ток в неразветвленной части цепи можно найти как сумму токов в ветвях
i (t) = i 1(t) + i 2(t)
Находим токи i 1(t) и i 2(t).
Определяем ток индуктивности в виде суммы принужденной и свободной составляющих:
i 1(t) = iL (t) = i 1 пр + i 1 св.
Принужденная составляющая – это ток в послекоммутационном установившемся режиме (при t = ∞). Для постоянного тока емкость представляет разрыв цепи, а индуктивность – короткое замыкание. Схема будет иметь вид, представленный на рис.3.4.2.
| U |
| R1 |
| L |
| iпр |
| i1пр |
| R2 |
| uCпр |
| С |
| S |
| Рис.3.4.2. |
Принужденная составляющая индуктивного тока будет равна общему току цепи в установившемся режиме. 
.
Для определения свободной составляющей составим характеристическое уравнение схемы через входное сопротивление:
Произведем замену jw → p, где 
- символ дифференцирования.
.
Дробь равняется нулю, если нулю равен числитель
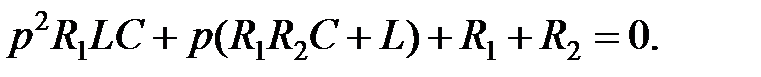
Запишем приведенное уравнение:
Получили квадратное уравнение относительно р. Корни уравнения находим из выражения:
. (3.2)
Подставляя численные значения параметров, получаем
с-1, 
с-1.
Решение для свободной составляющей определяется корнями характеристического уравнения.
В случае действительных и различных корней переходной процесс апериодический, решение ищется в виде:
В случае равных корней переходной процесс критический, решение будет иметь вид:
В случае комплексно-сопряженных корней переходной процесс периодический, решение имеет вид:
где А 1, А 2, А 3, … – постоянные интегрирования.
|
|
|
В нашем случае корни действительные и различные, переходной процесс апериодический, следовательно, свободную составляющую ищем в виде: 
.
Ток в ветви с индуктивностью определится выражением:
Для определения постоянных интегрирования А 1 и А 2необходимо найти производную от тока индуктивности:
Запишем уравнения для тока и его производной в начальный момент времени t = 0.
.
Определим i 1(0)и 
, для этого составим уравнение по второму закону Кирхгофа для контура R 2 → L → C:
, при t =0 → 
.
В первый момент после замыкания ключа емкость представляет собой короткое замыкание, а индуктивность разрыв цепи (рис.3.4.3).
| U |
| R1 |
| L |
| i (0) |
| i 1(0) |
| R2 |
| i 2(0) |
| С |
| S |
| Рис.3.4.3. |
Так как в цепи были нулевые начальные условия, то в момент времени t = 0 согласно (3.1) i 1(0+) = i 1(0-) = 0. Тогда i 1(0)· R2 = 0.
По второму закону коммутации uC (0+) = uC (0-) = 0. Cледовательно,
=0. (3.3)
Система уравнений для тока индуктивности и его производной в начальный момент времени будет иметь вид:
.
Решая эти уравнения относительно А 1 и А 2 находим:
А 1 = -1,98, А 2 = 0,29.
Ток i 1(t),будет изменяться по закону:
.
Найдем ток i 2(t). Так как начальные уравнения можно записать только для независимых переменных (iL (t) или uC (t)), то сначала определяем напряжение на емкости, которое представим в виде суммы принужденной и свободной составляющих.
uC (t) = uСсв + uCпр.
Принужденная составляющая определяется в установившемся режиме:
uCпр = i 1 прR2= 1,69·80 = 135,2 B.
Свободная составляющая:
.
Тогда 
.
Для определения постоянных интегрирования запишем производную напряжения uC (t):
.
Найдем значения напряжения на емкости и его производной в начальный момент времени t = 0.
По второму закону коммутации uC (0+) = uC (0-) = 0.
Составим уравнение по первому закону Кирхгофа: i (t) = i 1(t) +i 2(t). Учитывая, что 
, получим: 
.
В момент времени t = 0 по первому закону коммутации ток
i 1(0+)= i 1(0-) = 0, следовательно (см. рис.3.2.3), i (0+) = i 2(0+) = U/R 1.
|
|
|
Подставив числовые значения, получим:
Отсюда
(3.4)
Запишем систему уравнений для начального момента времени t = 0:
.
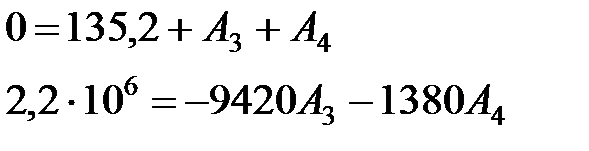Решая эту систему уравнений, находим: А3 = -250,43; А4 = 115,23.
Подставим значения постоянных интегрирования в выражения для напряжения и тока емкости.
В.
Ток в неразветвленной части цепи:
|
|
|
