 |
Операторный метод для действительных корней.
|
|
|
|
Составим операторную схему замещения (рис.3.4.4).
| S |
|
| I 1(p) |
| I (p) |
| I 2(p) |
| R2 |
| Lp |
| Li 1(0) |
| R1 |
|
|
| Рис.3.4.4. |
До коммутации тока в катушке и напряжения на конденсаторе не было. Это значит, что в цепи нулевые начальные условия uC (0) = 0 и i 1(0) = 0. Изображение тока i (t) 
I (p)запишем по законуОма:
, где р = σ+jω – оператор Лапласа.
Изображение постоянного напряжения U есть
.
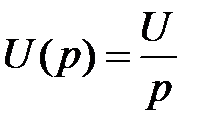Операторное сопротивление Z(p) равно
.
Тогда,
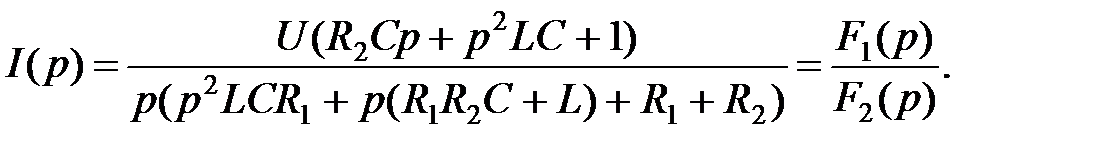(3.5)
Подставив числовые значения, получим:
Изображение тока представляет собой отношению двух функций переменного р, причем степень многочлена F 2(р)больше степени многочлена F 1(p), то есть I (p) представляет собой правильную дробь.
Для того чтобы вычислить оригинал - ток i (t), нужно воспользоваться формулой разложения. С этой целью нужно сначала найти корни знаменателя. К двум корням, которые мы вычислили в классическом методе: p 1 = -9420 р 2 = -1380, добавился третий корень р 3 = 0. Наличие нулевого корня свидетельствует о существовании принужденной составляющей.
Оригинал тока находим, используя формулу разложения:
Здесь F 3(p) = F 2 /p = 10-5 p 2 + 0,108 p + 130.
Определим производную знаменателя:
.
Подставляя в выражения для F 1(p) и F 3’(р) значения корней, подсчитаем соответственно F 1(рк)и F 3’(рк):
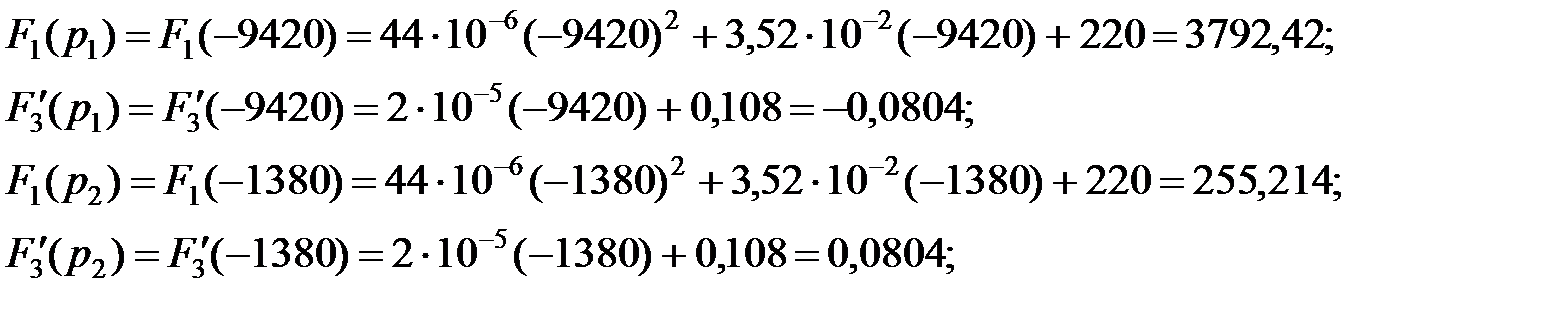
Окончательно получим:
Результат идентичен полученному классическим методом.
На примере той же схемы (рис.3.4.1) рассмотрим случай комплексно-сопряженных корней.
Параметры цепи:
U = 220 B
R1 = 50 Ом
R2 = 100 Ом
L = 50 мГн =5·10-2 Г
С = 8 мкФ = 8·10-6 Ф
Классический метод для комплексно-сопряженных корней.
Ищем решение для тока i 1(t)как сумму принужденной и свободной составляющих
|
|
|
i 1(t) = iL (t) = i 1 пр + i 1 св.
Принужденные составляющие определяются в установившемся режиме
.
Корни характеристического уравнения находим из выражения (3.2):
.
Подставляя значения параметров, получим:
p 1,2 = -2250 ± j 1561,25.
Так как корни комплексно-сопряженные, свободную составляющую ищем в виде:
Здесь δ = 2250, ωсв = 1561,25, тогда
i 1(t) = 1,467 + 
Для определения постоянных А 1 и γ запишем производную тока i 1(t)
В момент времени t = 0 согласно условий (3.1) и (3.3) имеем:
i 1(t) = 0 и 
.
Постоянные определяем, решая систему уравнений для тока и его производной в момент времени t = 0.
Из первого уравнения:
.
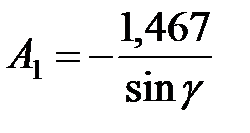Подставляем А 1 во второе уравнение:
Отсюда
, 
Ток i 1(t):
.
Для определения тока i 2(t) запишем уравнения для независимой переменной uC (t) и ее производной:
В начальный момент времени 
t = 0 по условию (3.1) uC (t) = 0, производная, согласно (3.4) равна
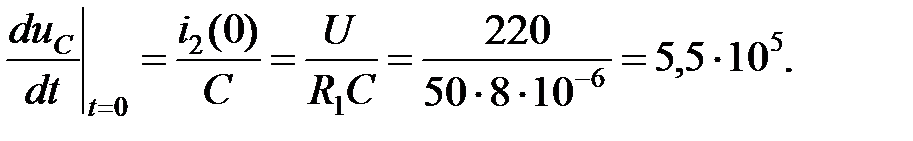
С учетом этого для t = 0 имеем:
.
Из первого уравнения:
.
Подставляем во второе уравнение
Отсюда
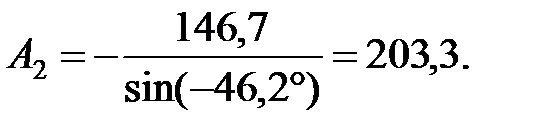
=C[ 
]=
Преобразуем выражение в квадратных скобках.
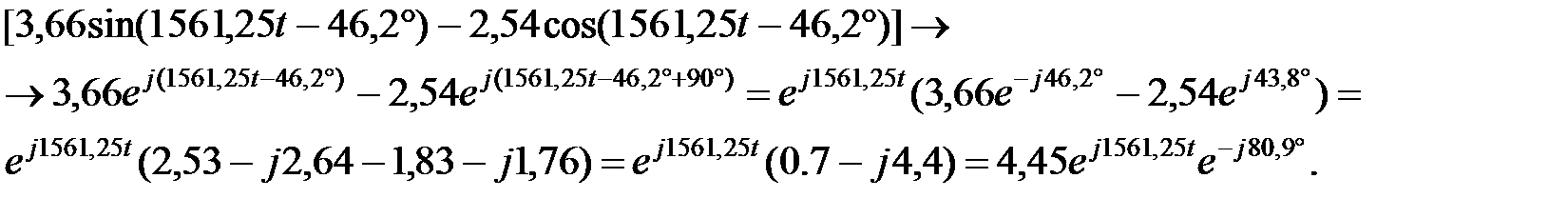
Окончательно ток запишется:
Ток в неразветвленной части цепи:
Преобразуем выражение в скобках.
Окончательный результат
.
Операторный метод для комплексно-сопряженных корней.
Ток в неразветвленной части цепи определится выражением (3.5)
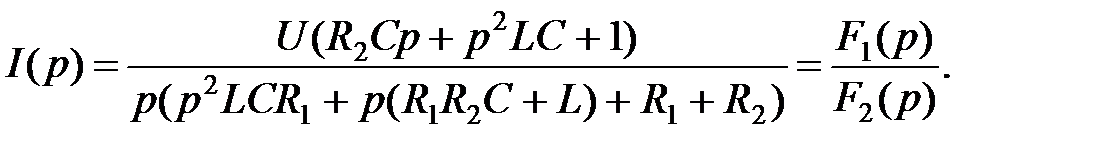
Подставив числовые значения, получим:
Находим корни уравнения F 2(p) = 0.
p 1,2 = -2250 ± j 1561,25; p 3 = 0.
Так как корни комплексно-сопряженные, оригинал тока находим, используя формулу разложения:
(3.6)
.
Подставляя в выражение для F 1(p) и F 3’(р) значения корней, подсчитаем соответственно F 1(рк)и F 3’(рк):
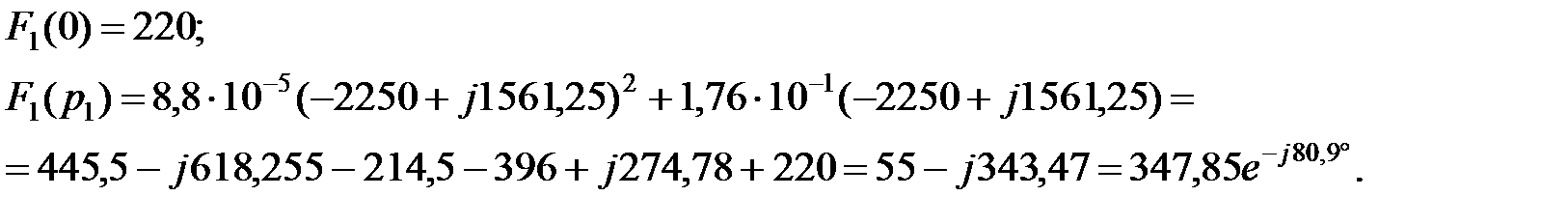
F 3(0) = 150;
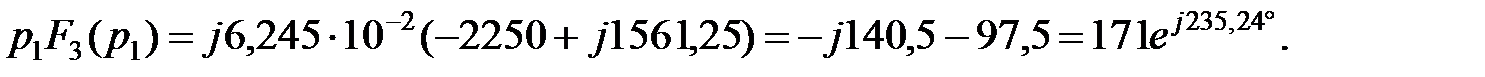
Подставляем полученные выражения в формулу (3.6)
Используя правила тригонометрии, преобразуем
Окончательный результат
Требования к защите курсовой работы.
При защите работы студент должен уметь грамотно объяснить последовательность выполнения расчетов, рассказать, какими правилами и законами электрических цепей он воспользовался на каждом этапе расчетов, обосновать правомерность их применения, и уметь демонстрировать их на других примерах.
|
|
|
Оценка за курсовую работу ставится по итогам защиты.
|
|
|
