 |
В качестве первого размещённого элемента примем разъём Х1 (позиция 1)
|
|
|
|
Рассчитываем коэффициенты относительной внешней связанности по формуле (8).
.
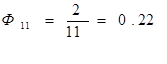На данном этапе будем размещать элемент с максисальным значением Фi, т. е. микросхему DD11.
Рассчитываем прирощение функции цели для незанятых ячеек печатной платы по формуле (9).
ΔF2=2 ΔF3=2 ΔF4=2 ΔF5=4 ΔF6=4 ΔF7=4 ΔF8=6 ΔF9=6 ΔF10=6 ΔF11=8 ΔF12=8.
Выбираем минимальное значение Fi ,т. е. вторую.
В качестве первого размещённого элемента примем разъём Х1 (позиция 1) и DD 11 (позиция 2)
Рассчитываем коэффициенты относительной внешней связанности по формуле (8).
.
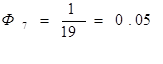
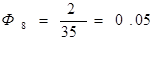
На данном этапе будем размещать элемент с максисальным значением Фi, т. е. микросхему DD1.
Рассчитываем прирощение функции цели для незанятых ячеек печатной платы по формуле (9).
ΔF3=С1х1d13+C111d23=3*1+3*1=6;
ΔF4= С1х1d14+C111d24=3*1+3*2=9;
ΔF5= С1х1d15+C111d25=3*2+3*1=9;
ΔF6= С1х1d16+C111d26=3*2+3*2=12;
ΔF7= С1х1d17+C111d27=3*2+3*3=15;
ΔF8= С1х1d18+C111d28=3*3+3*2=15;
ΔF9= С1х1d19+C111d29=3*3+3*3=18;
ΔF10= С1х1d110+C111d210=3*3+3*4=21;
ΔF12= С1х1d112+C111d212=3*4+3*4=24;
Выбираем минимальное значение Fi ,т. е. третью.
Результаты размещения
| Микросхема | Номер посадочного места |
| Х1 | 1 |
| DD1 | 3 |
| DD2 | 4 |
| DD3 | 8 |
| DD4 | 9 |
| DD5 | 5 |
| DD6 | 6 |
| DD7 | 7 |
| DD8 | 10 |
| DD9 | 11 |
| DD10 | 12 |
| DD11 | 2 |
Трассировка цепей питания и земли с использованием алгоритма построения кратчайших связывающих цепей
Трассировка – прокладка электрических трасс, проводов (при проводном монтаже), дорожек.
Трассировку соединений осуществляют с помощью алгоритмов, основанных на методах динамического программирования. Общим для этих алгоритмов является разбиение монтажного поля на ячейки, размер и форма которых определяют плотность и конфигурацию печатных проводников. Наибольшее распространение на практике получило разбиение рабочего поля на правильные квадраты, что обеспечивает простую адресацию ячеек в прямоугольной системе координат и привычную форму соединений. Размеры ячеек определяются конструктивно – технологическими требованиями, предъявляемыми к печатному монтажу. Так как в каждой ячейке обычно размещается только один вывод или печатный проводник, максимальные размеры ячеек определяются допустимой точностью воспроизведения проводников.
|
|
|
Алгоритм Краскала (цепи земли)
Строится кратчайшая связывающая сеть путем последовательного присоединения к ней ребер, удовлетворяющих следующим условиям:
- ребро минимально
- ребро инцидентно только по одной вершине
- присоединение рассматриваемого ребра не приводит к повышению степени любой вершины больше заданного числа
Последовательность:
- на множестве вершин строится полный граф, задаются матрица расстояний
- упорядочиваются ребра в порядке возрастания их длины
Построение КСС осуществляется путем последовательного выбора ребер удовлетворяющих трем условиям, при этом формируется массив индексов ребер. Условием получения покрывающего дерева является вычерчивание всех номеров вершин в массиве номеров.
1) Матрица расстояний
|
x1 | DD11 | DD5 | DD3 | DD9 |
| DD1 | DD6 | DD4 | DD10 | |
| DD2 | DD7 | DD8 |
Рис.4
Матрица длин
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | p | |
| 1 | 0 | 1 | 1 | 1 | 2 | 2 | 2 | 3 | 3 | 3 | 4 | 4 | 30 |
| 2 | 1 | 0 | 1 | 2 | 1 | 2 | 3 | 2 | 3 | 4 | 3 | 4 | 31 |
| 3 | 1 | 1 | 0 | 1 | 2 | 1 | 2 | 3 | 2 | 3 | 4 | 3 | 27 |
| 4 | 1 | 2 | 1 | 0 | 3 | 2 | 1 | 4 | 3 | 2 | 5 | 4 | 31 |
| 5 | 2 | 1 | 2 | 3 | 0 | 1 | 2 | 1 | 2 | 3 | 2 | 3 | 26 |
| 6 | 2 | 2 | 1 | 2 | 1 | 0 | 1 | 2 | 1 | 2 | 3 | 2 | 22 |
| 7 | 2 | 3 | 2 | 1 | 2 | 1 | 0 | 3 | 2 | 1 | 4 | 3 | 26 |
| 8 | 3 | 2 | 3 | 4 | 1 | 2 | 3 | 0 | 1 | 2 | 1 | 2 | 27 |
| 9 | 3 | 3 | 2 | 3 | 2 | 1 | 2 | 1 | 0 | 1 | 2 | 1 | 23 |
| 10 | 3 | 4 | 3 | 2 | 3 | 2 | 1 | 2 | 1 | 0 | 3 | 2 | 27 |
| 11 | 4 | 3 | 4 | 5 | 2 | 3 | 4 | 1 | 2 | 3 | 0 | 1 | 29 |
| 12 | 4 | 4 | 3 | 4 | 3 | 2 | 3 | 2 | 1 | 2 | 1 | 0 | 30 |
|
|
|
2) строки упорядочиваются по возрастанию массив ребер число ребер
В результате трассировки цепей земли будет иметь вид:
x1 | DD11 | DD5 | DD3 | DD9 | |||
| DD1 | DD6 | DD4 | DD10 | ||||
| DD2 | DD7 | DD8 |
Рис.5
Алгоритм Прима (цепи питания)
В алгоритме Прима производится манипуляция с матрицей расстояний. Например: выбирается произвольная вершина (строка матрицы), в ней просматриваются элементы и выбирается наименьший присоединяется ближайшая вершина после чего обнуляется столбец, соответствующий присоединенной вершине. На следующем этапе просматриваются уже две строки и процедура повторяется. Проверка ограничения максимально допустимой степени вершины осуществляется аналогично алгоритму Краскала (анализируется массив индексов выбранных вершин)
1) матрица расстояний используется та же, что и в алгоритме Краскала (см. выше)
2) выбирается произвольно вершина (например № 1), где минимум элемент
В результате всех этих действий получаем трассировку цепей питания в следующем виде.
|
x1 | DD11 | DD5 | DD3 | DD9 |
| DD1 | DD6 | DD4 | DD10 | |
| DD2 | DD7 | DD8 |
Рис.6
4. Трассировка сигнальных цепей с помощью волновых алгоритмов
Данный алгоритм является классическим примером использования методов динамического программирования для решения задачи трассировки печатных соединений. Основные принципы построения трасс с помощью волнового алгоритма сводятся к следующему.
Все ячейки монтажного поля подразделяют на занятые и свободные. Занятыми считаются ячейки, в которых уже расположены проводники, построенные на предыдущих шагах, или находятся монтажные выводы элементов, а также ячейки, соответствующие границе платы запрещенным для прокладывания проводников участкам. Каждый раз при проведении новой трассы можно использовать лишь свободные ячейки, число которых по мере проведения трасс сокращается.
На множестве ячеек (свободных) коммутационного поля моделируют волну влияния из одной ячейки в другую, соединяемых впоследствии одним проводником. Первую ячейку, в которой зарождается волна влияний называют источником, а вторую – приемником волны. Чтобы иметь возможность следить за прохождением фронта волны влияний, его фрагментом на каждом этапе присваивают некоторые веса:
|
|
|
(10)
где 
и 
- веса ячеек k – го и (k-1) –го фронтов;
φ – числовая характеристика, зависящая от выбранного критерия оптимизации;
На накладывают одно ограничение – веса ячеек предыдущих фронтов не должны быть больше весов ячеек последующих фронтов. Фронт распространяется только на соседние ячейки, которые имеют с ячейками предыдущего фронта либо общую сторону, либо хотя бы одну общую точку. Процесс распространения волны продолжается до тех пор, пока ее расширяющийся фронт не достигнет приемника или на θ шаге не найдется ни одной свободной ячейки, которая могла бы быть включена в очередной фронт, что соответствует случаю невозможности проведения трассы при заданных ограничениях.
Если в результате распространения волна достигла приемника, то осуществляют «проведение пути», которое заключается в движении от приемника к источнику по пройденным на этапе распространения волны ячейкам, следя за тем, чтобы значение монотонно убывали. В результате получают путь, соединяющий эти две точки. Из описания алгоритма следует, мято все условия, необходимые для проведения пути, закладываются в правила приписания веса ячейкам.
Приведем два примера трассировки соединений с помощью волнового алгоритма ЛИ.
Чтобы исключить неопределенность при проведении пути для случая, когда несколько ячеек имеют одинаковый минимальный вес, вводят понятие путевых координат задающих предпочтительность проведения трассы.
В приложении 5 представлена плата с проведенной трассировкой.
| 7 | 6 | 5 | 4 | 3 | 4 | 5 | 6 |
| ||||||||||
| 6 | 5 | 4 | 3 | 2 | 3 | 4 | 5 |
| ||||||||||
| 5 | 4 | 3 | 2 | 1 | 2 | 3 | 4 |
| ||||||||||
| 4 | 3 | 2 | 1 | 0 | 1 | 2 | 3 |
| ||||||||||
| 5 | 4 | 3 | 4 |
| ||||||||||||||
| 6 | 5 | 6 | 7 | 8 | 4 | 5 |
| |||||||||||
| 7 | 6 | 7 | 8 | 9 | 5 | 6 |
| |||||||||||
| 8 | 7 | 8 | 9 | 10 | 6 | 7 |
| |||||||||||
| 9 | 8 | 9 | 10 | 11 | 9 | 8 |
| |||||||||||
| 10 | 9 | 10 | 11 | 12 | 11 | 10 | 9 |
| ||||||||||
|
| ||||||||||||||||||
|
| ||||||||||||||||||
|
| ||||||||||||||||||
|
| ||||||||||||||||||
|
| ||||||||||||||||||
|
| ||||||||||||||||||
|
| ||||||||||||||||||
| 4 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ||||||||||
| 10 | 9 | 8 | 7 | 6 | 5 | 3 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ||||
| 11 | 4 | 2 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ||||||||
| 12 | 13 | 14 | 17 | 3 | 2 | 1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 6 | ||||
| 13 | 14 | 15 | 16 | 5 | 6 | 7 | 8 | |||||||||||
| 14 | 15 | 16 | 15 | 14 | 13 | 12 | 11 | 10 | 9 | 8 | 7 | 6 | 7 | 8 | 9 | |||
Литература
1. Мельничук В.В. «Конспект лекций по АКИТ и ПРЭС» БГУИР Минск 2000г.
2. Деньдобренько Б.Н. «Автоматизация конструирования РЭА» Москва 1980г.
3. Методическое пособие к лабораторному практикуму по курсу «Математическое обеспечение конструкций и технологии проектирования с применением САПР» Минск 1987г.
|
|
|
