 |
Математическая модель химически-активного многокомпонентного пограничного слоя
|
|
|
|
Выразим температуру, давление и скорость как функции, зависящие от координат и времени.
; 
; 
(11)
Для определения 3х неизвестных в форме зависимостей (11) необходимо иметь 3 уравнения, которые должны представлять математическую модель пограничного слоя. Модель выводится на базе использования основных законов физики – сохранение массы, количества движения, энергии, которые записываются применительно к движущемуся газовому потоку в виде нелинейных дифференциальных уравнений неразрывности, движения и энергии. Однако этих уравнений недостаточно для определения полей температуры, давления, скорости. Поэтому к 3м уравнениям необходимо добавить законы, характеризующие процессы внутреннего трения и теплопроводности. Рассмотренная выше физико-химическая модель переноса теплоты и массы на непроницаемой стенке многокомпонентном ламинарном пограничном слое базируется на постулате Прандтля. Согласно этому постулату все процессы переноса реализуются только в пределах тонких пристеночных слоев. Вне этих слоев, вдоль поверхности обтекаемого тела, осуществляется только конвективный перенос массы и энергии непосредственно набегающим потоком.
Ответственными за процессы переноса тепло- массообмена у стенки являются 3 рода пограничных слоев:
1. Динамический
2. Тепловой
3. Диффузионный
1) Динамический пограничный слой (двухмерная модель)
Пограничный слой, в котором градиенты компонентов вектора скорости
в нормальном направлении значительно превышает градиенты этих величин в касательных направлениях.
С увеличением скорости потока толщина динамического пограничного слоя уменьшается вследствие сдувания его потоком. Напротив, с увеличением вязкости толщина динамического слоя увеличивается.
|
|
|
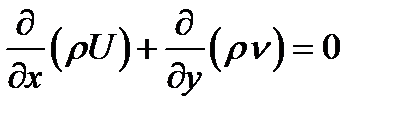- уравнение неразрывности (12)
- относительно оси Ох (13)
- относительно Оу (14)
2) Тепловой пограничный слой-это
Пограничный слой, в котором градиент энтальпии или температуры в нормальном направлении значительно превышает градиенты этой величины в касательных направлениях.
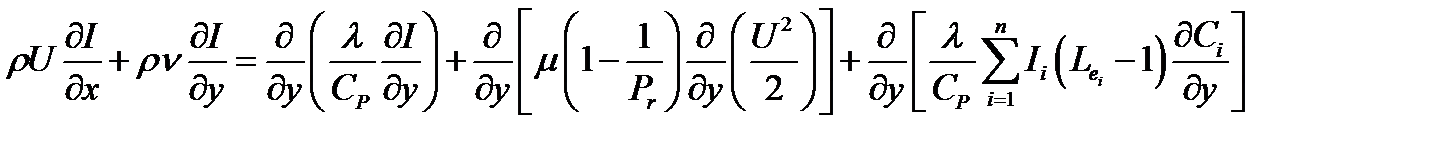
(15)
; I – энтальпия
Ii – энтальпия образования i-компоненты
- теплопроводность
Сi – концентрация i-компоненты
- коэффициент динамической вязкости
- отношение диффузионных потоков к тепловым потокам
Di – диффузионный коэффициент из закона Фика
; 
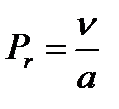(16)
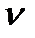- динамические потоки
а – коэффициент теплопроводности
Для передней критической точки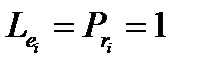 
, следовательно
(замороженный пограничный слой)
; 
(17)
3) Диффузионный пограничный слой
Посредством диффузии, часть набегающего потока переходит во внешний защитный пограничный слой.
(18)
- скорость образования i-компоненты
Скорость образования в равновесном пограничном слое стремится к нулю.
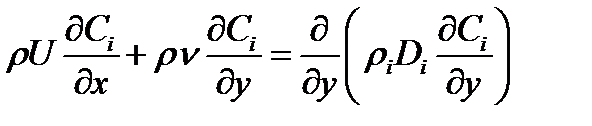(19)
4) Уравнение Клапейрона-Менделеева – формула, устанавливающая зависимость между давлением, молярным объемом и абсолютной температурой газа.
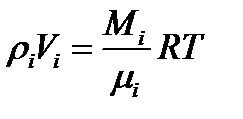(20)
5) Условие на поверхности стенки
y=0: U=0, 
=0, I=Iw (энтальпия стенки), Ci=Cwi
6) Условие на границе ударной волны происходит диффузия
|
|
|
: U=0, 
= 
, Ci =Ci0
Закон Фика - количественно описывает процесс диффузии и отражает тот факт, что поток вещества I в направлении оси y пропорционален градиенту концентрации dC / d y
(21)
В следствие того, что данная математическая модель химически-активного многокомпонентного пограничного слоя является трехмерной, достаточно сложной и точность ее решения выше потребной точности решения для практических инженерных задач, мы можем воспользоваться более простым, но менее точным методом.
|
|
|
