 |
Внутренняя задача теплообмена
|
|
|
|
Внутренняя задача теплообмена – это определение температуры по всей толщине защитного слоя. Существует три вида теплопередачи — лучистая теплопередача, конвекция и теплопроводность. Лучистая теплопередача и конвекция не учитываются в силу малости их величин. При этих упрощающих допущениях проведем решение задачи в одномерной модели:
(23)
- теплопроводность
С - теплоемкость
Область определения:
- продолжительность прогрева 
L – толщина материала 
Зададим начальные условия (распределение поля температур Т):
; 
при 
= 0
Граничные условия на внешней границе определим из решения внешней задачи (22):
(24)
Внутренние граничные условия:
; при q 2 = 0
При этом на температуру поверхности накладываем ограничения:
Tmax 
Tкр ; Tкр = ТАМГ6 (
0,2) = 373К
Для решения системы дифференциальных уравнений (25) используем метод конечных разностей (нестационарная задача). Этот метод основан на том, что искомая характеристика ищется не в виде непрерывной функции, а в узлах области поиска решения:
(25)
Для аппроксимации системы (25) осуществляется по неявной схеме. Геометрическое представление неявной схемы приведено на рисунке 1. Шаги по пространству и времени рассчитываются по формулам (2.5.4).
0 (рис.1)
- шаг ; 
(26)
|
|
|
N – количество узлов по пространству 
М – количество узлов по времени 
Нумерация узлов по пространству:
Индекс i – по времени j, тогда в соответствующих узлах обозначение температуры и координат будут иметь вид:
; 
Переходим от дифференциальных операторов к алгебраическим:
(27)
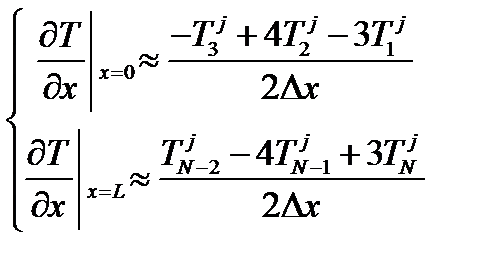(28)
За счет подстановки формул (27) и (28) в систему (25) переходим к ее алгебраической записи:
(29)
(30)
(31)
Приведем систему уравнений (29 - 31) к виду 3-х диагональной матрицы:
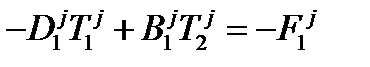(32)
(33)
(34)
Для этого необходимо расчисть разностные коэффициенты входящие в (32)-(34). Формулы для расчета разностных коэффициентов уравнения (33) могут быть получены путем перегруппировки слагаемых в уравнении (30):
(35)
Для расчета разностных коэффициентов в уравнении (33) выразим T3 из уравнения (30) для второго узла.
(36)
и подставим в (30). После преобразования получим:
(37)
Сопоставим полученное уравнение с (37) и перегруппировав слагаемые в уравнении получим формулы для расчета разностных коэффициентов уравнения (32)
(38)
|
|
|
Подобным образом преобразуем уравнение (34) и получаем формулы для расчета разностных коэффициентов:
(39)
Для расчета температуры в узлах разностной сетки на текущем временном слое используется метод прогонки. В методе прогонки для расчета температуры применяется формула:
(40)
где 
- прогоночные коэффициенты
Уравнения (40) и (32) с математической точки зрения формально одинаковы. Сопоставив их между собой, найдем выражения для расчета прогоночных коэффициентов 
и 
.
(41)
Для расчета прогоночных коэффициентов и , запишем уравнение (33) для второго узла.
(42)
В этом уравнении выразим Т1 через формулу (41) с уже рассчитанными прогоночными коэффициентами. Произведя группировку слагаемых при Т2 и Т3 получим формулы для вычисления прогоночных коэффициентов во втором узле:
Аналогичные соображения применяются для получения формул во всех последующих узлах. В этом случае формулы для расчета прогоночных коэффициентов можно записать в универсальном виде:
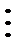
(42)
Для расчета значения температуры ТN произведем подстановку в уравнение (34) формулы (41) для N-1 узла:
(43)
Рассчитываем поле температур:
Ti = 
Ti-1 + 
; i = N -1,1.
Переходим к расчету профиля температуры на следующем временном слое.
Таким образом, получим значение Tij, i =1, N, j = 1, M во всех узлах области поиска решения.
|
|
|
