Марковские случайные процессы .

Задачи ТМО

При исследовании операций часто приходится сталкиваться с работой систем, в которых в той или иной форме производится «обслуживание» потока однородных требований (заявок).

Например: АТС, магазины, различные технические системы, системы военного назначения и т.п.

Такие системы обычно рассматривают как Системы Массового Обслуживания (СМО).

Каждая СМО состоит из какого-то числа обслуживающих единиц, которые называются каналами обслуживания.

Например: линии связи, продавцы, пункты технического обслуживания и т.п.

По числу каналов обслуживания СМО могут быть одноканальными и многоканальными.

Требования на обслуживание или заявки поступают в систему в какие-то случайные моменты времени. Обслуживание заявки продолжается, в общем случае, также какое-то случайное время T_{обс .}, после чего канал освобождается и готов к приему следующей заявки. Случайный характер потока заявок и времени обслуживания приводит к тому, что в какие-то периоды времени на входе СМО скапливается излишне большое число заявок, и они либо становятся в очередь, либо покидают систему необслуженными. В другие периоды времени система может работать с недогрузкой, либо и вовсе простаивать.

Например:

1. АТС – многоканальная система, в которую поступают вызовы от абонентов на обслуживание (соединение с другим абонентом). Если каналы (линии связи) занят, то при наборе первых [трех] цифр возникает сигнал «занято» и заявка получает отказ. Очередь на обслуживание отсутствует.

2. Обслуживание M станков-автоматов N рабочими (N≤ M). В их обязанности входит контроль, наладка станков, заправка их сырьем, устранение неисправностей и т.п. Каждый рабочий одновременно может обслуживать только один станок. Если число отказавших станков больше числа рабочих (каналов обслуживания), то образуется очередь на обслуживание.

3. Система передачи сообщений (например: РТС, селектор). В этом случае возможно ожидание на входе в систему – образование очереди, максимальная длина которой определяется техническими возможностями системы и ограничена. Кроме того, в зависимости от важности сообщений, они могут обслуживаться как в порядке поступления, так и вне очереди (с приоритетом) прерывая при ней идущие сообщения.

Кроме того в реальных системах могут встречаться и другие условия функционирования систем.

Например: ограничение времени нахождения заявки в очереди, поступление заявок группами и т.д.

Процесс функционирования СМО представляет собой случайный процесс с дискретными состояниями и непрерывным временем. Состояние системы (число занятых каналов, число заявок в очереди и т.п.) изменяется скачкообразно в моменты появления каких-либо событий – приход очередной заявки, окончание обслуживания заявки и т.п.

Предметом ТМО является построение математических моделей, связывающих заданные условия работы СМО (число каналов обслуживания, их производительность, правила обслуживания и т.п.) с интересующими нам показателями эффективности ее работы (среднее число заявок, обслуживаемых системой за указанный период, среднее число занятых каналов, средняя длина очереди, вероятность обслуживания заявки в системе, среднее время ожидания обслуживания и т.п.). Т.е. аппарат ТМО позволяет решать прямые задачи исследования операций. Математический анализ СМО существенно упрощает, если процесс ее работы Марковский. Процесс называется Марковским, если вероятностные характеристики его в будущем зависят только от состояния процесса в настоящем. При этом не важно, каким путем оно в это состояние пришло, - т.е. не важно какое его состояние было в прошлом.

Такие процессы называются процессами без памяти (условие марковости процесса функционирования СМО рассмотрим ниже). Если же свойство марковости процесса нарушается, то математическое его описание существенно усложняется и получить его аналитическое описание удается лишь в редкий случаях, зачастую достаточно приближенно. Тогда для определения характеристик СМО (решение прямой задачи СМО) широко используется построение имитационных моделей.

Решение обратных-оптимизационных задач ИО для СМО, т.е. поиск наилучших параметров системы – числа каналов обслуживания, их производительности, дисциплины обслуживания и т.п. – с таким уровнем выбранного критерия эффективности системы в целом рассматривается обычно как отдельная задача. В ней модели ТМО используются для определения значений критерия эффективности системы или заданного значения ее параметров.

Оптимизация работы СМО может производиться под разными углами зрения: с точки зрения ее «владельца» и с точки зрения «клиентов». При этом перекос в ту или иную сторону может привести к победам для другой стороны.

Поэтому при выборе критерия эффективности необходимо учитывать интересы обеих сторон и задача оптимизации СМО решается как многокритериальная.

 

Структура СМО и ее основные характеристики

 

В общем виде СМО можно представить как:

 

Выходной поток требований

Входной поток требований

Система обслуживания

 

 

Входной поток требований – случайная исследовательность требований, поступающих на обслуживание. Его основные характеристики:

· распределение числа требований в единицу времени;

· распределение времени между двумя соседними требованиями;

· ограниченность потока (ограничен, неограничен).

Система обслуживания характеризуется:

· механизмом обслуживания и дисциплиной обслуживания.

Механизм обслуживания задается:

· распределением времени обслуживания;

· пропускной способностью (число каналов обслуживания);

· доступностью для обслуживания (полнодоступные – возможны всегда и неполнодоступные – обслуживание лишь в определенные периоды).

Дисциплина обслуживания – регламентирует порядок поступления требований на обслуживание из очереди:

-без приоритетов – все время в одинаковом порядке (первый пришел – первый обслужился, последний пришел – первый обслужился и т.д.).

- с приоритетами, - когда порядок обслуживания определяется не местом в очереди, а рангом требования. При этом приоритеты бывают:

1.абсолютные – требование более высокого ранга исключает из идущего обслуживания требования меньшего ранга;

2.относительные - начинает обслуживаться раньше требований низкого ранга.

 

По способу образования очереди СМО делятся на системы с потерями и без потерь.

 

1. системы с потерями (отказами) или системы без ожидания. В них требование, поступившее в систему в момент, когда все каналы заняты, покидает систему.

Эффективность функционирования таких систем характеризуется:

-вероятностью потери требования (отказа);

-среднее число отказов за заданный временной интервал;

-среднее число занятых каналов;

 

2. системы без потерь (отказов) или системы с ожиданием. В них, в случае, если все каналы заняты, требования становятся в очередь на обслуживание. Длина очереди и время ожидания не ограничены.

Они характеризуются:
-средней длиной очереди;

-средним временем ожидания обслуживания;

-средним числом занятых каналов.

 

3. смешанные системы. В них накладываются ограничения на длину очереди, время пребывания в очереди, время обслуживания. Для них дополнительно могут использоваться следующие характеристики:

-среднее число требований, покинувших систему до начала обслуживания;

-среднее число требований, покинувших систему во время обслуживания;

-время обслуживания требований, покинувших систему во время обслуживания.

Выходной поток требований – образуется требованиями, покидающими систему как обслуженными, так и не обслуженными из очереди или каналов обслуживания. Описывается теми же статистическими характеристиками, что и входной поток.

 

Схематически СМО можно представить в виде

Для удобства в 1953 году Д.Г.Кендаллом была введена следующая система обозначений для подобных СМО.

a/b/n

где: а – вид распределения моментов времени поступления заявок на обслуживание;

b – вид распределения времени обслуживания заявок в канале обслуживания;

n – число каналов обслуживания.

Для обозначения вида закона распределения входного потока и потока обслуживания обычно используют следующие обозначения:

М – марковское – exp закон распределения интервалов времени между требованиями входными и обслуженными.

D – детерменированные интервалы времени между требованиями

Е_к - распределение Эрланга К-ого порядка

G – произвольный закон распределения

 

Кроме этого дополнительно указывают

m – максимальную длину очереди (максимальное число требований в системе)

d – дисциплину организации очереди (первым пришел – первым обслужился – без приоритета; последним пришел – первым обслужился – с приоритетом и др), а также другую информацию.

 

Одним из важнейших факторов, определяющих возможность нахождения основных характеристик СМО аналитически является вид потоков требований на входе системы и обслуживания.

Рассмотрим их.

 

Входной поток требований

Регулярный (детерменированный) поток

В нем требования поступают в систему через одинаковые неслучайные моменты времени по одному (в общем случае – пакетами). Интенсивность потока – число требований, поступающих в единицу времени будет

Где а – интервал времени между двумя соседними требованиями.

Примерами такого потока служат: движение поездов через станцию строго по расписанию, поток деталей на конвейере…

СМО с детерминированным потоком рассчитываются достаточно просто. Обычно в случае нарушения детерминированности результаты расчета оказывается непригодны.

Простейший поток

Наиболее распространенная форма описания входного потока, позволяющая достаточно просто исследовать СМО аналитически.

Под простейшим потоком понимается случайный поток требований, обладающий свойствами стационарности, ординарности и отсутствия последействия.

Стационарность означает, что статистические характеристики потока (распределение числа требований в единицу времени, распределение интервала между соседними требованиями) во времени не меняются.

Ординарность означает практическую невозможность одновременного появления двух и более требований. Т.е. вероятность появления двух и более требований на интервале ∆t→0 бесконечно мала по сравнению с вероятностью появления одного требования

 

Отсутствие последействия означает, что вероятность появления К требований на интервале [t,t+τ] не зависит от числа требований, появившихся до момента t и положения интервала τ на временной оси.

 

Можно показать, что указанным свойствам отвечает Стационарный Пуассоновский поток требований со средним числом требований, поступающих в единицу времени λ=const.

 

Для него число требований, поступающих в течение заданного интервала времени τ, распределенных по закону Пуассона с параметром a= λ∙ τ, а вероятность, что на интервале τ возникнет ровно К требований равна

Согласно свойству закона Пуассона величина есть математическое ожидание и дисперсия числа требований, поступающих на интервале времени

Величина - одна из основных характеристик потока – интенсивность потока требований – математическое ожидание числа требований, поступающих в единицу времени.

Найдем закон распределения интервала времени между двумя соседними требованиями.

Пусть T – случайная величина – интервал между требованиями.

Вероятность того, что T примет значение больше или равно t равна вероятности того, что на интервале продолжительностью t не возникнет ни одного требования, т.е.

 

, где

 

Функция распределения длины интервала между требованиями,

 

а функция плотности распределения будет

 

 

Как видим это экспоненциальный закон распределения.

Его основные числовые характеристики:

Вид закона распределения не зависит от положения интервала между требованиями на временной оси (стационарность) и от того, появились или нет требования раньше (отсутсвие последействия). * Можно показать и выполнение условия ординарности.

 

* Экспоненциальный закон распределения обладает замечательным свойстовом.

Если промежуток времени, распределенный по exp закоону уже длился некоторое время , то это кикак не влияет на закон распределения оставшейся части промежутка: - он будет таким же, как и закон распределения всего промежутка T.

Этим свойством обладает только exp закон.

При анализе реальных выходных потоков оказывается, что простейший поток имеет широкое распространение на практике. Это обуславливается предельными свойствами простейшего потока, согласно которым он возникает при суммировании большого числа взаимно независимых потоков малой интенсивности, обладающих свойствами стационарности и ординарности, при этом свойство отсутствия последействия может не выполняться.

Другие виды входных потоков.

1. Нестационарный Пуассоновский поток

Если поток событий ординарный, без последействия, но с переменной плотностью числа событий, приходящихся на единицу времени

, то такой поток событий называется нестационарным Пуассоновским.

Для него число требований, поступающих на участке времени длиной , начинающемся в т. также подчинено закону Пуассона

но значение параметра зависит и от и от

Закон распределения интервала времени между двумя соседними требованиями отличается от экспоненциального и зависит от вида функции.

2. Поток с ограниченным последействием

Рассмотрим ординарный поток событий.

Здесь 1,2,3,… сообщения, T₁ , T₂ ,… интервалы времени между событиями.

* Поток отказов часто называют потоком восстановлений т.к. в момент отказа происходит мгновенное восстановление элемента.

Если интервалы времени между последовательными событиями представляют собой независимые сл. величины, то такой поток событий называется потоком с ограниченным последействием (поток Пальма).

Частным случаем потока Пальма является простейший поток.

Потоком Пальма является поток отказов (восстановленный) элементов в техническом устройстве, если отказы наступают независимо, а отказавший элемент мгновенно заменяется новым. (поток восстановленный см. * на обороте)

Потоком с ограниченным последствием будет является поток необслуженных заявок, покидающих систему:

Теорема Пальма

Если на вход СМО поступает поток заявок типа Пальма и в случае занятости каналов обслуживания заявка покидает систему необслуженной (получает отказ), а время обслуживания заявок в системе подчинено exp закону, то поток необслуженных заявок также является потоком Пальма (теор. Пальма)

Другим частным случаем потоков Пальма являются потоки Эрланга, которые образуются «просеиванием» простейшего потока.

Если из простейшего потока будем удалять требования через одно, то оставшиеся требования образуют поток Эрланга первого порядка, если будем удалять требования парами, оставляя каждое третье, то они образуют поток Эрланга второго порядка и т.п. Если из простейшего потока будем удалять требования группами по К штук в каждой группе, то оставшиеся требования образуют поток Эрланга k –го порядка (см. рис).

_*____*____*____*____*____*____*____*____*_____*__ Простейш. поток

_*_________*_________*_________*_________*________пот.Эрл.1-го по-ка

_*______________*______________*_______________*___ ---------- 2-го

_*___________________*___________________*__________ ---------- 3-го

 

Рассмотрим в качестве характеристики «меры случайности» коэффициент вариации

V_T =Ϭ _T /m _T, который применяется в ТВ для????? CВ

Для закона распределения Эрланга К-го порядка

V_T^(К)= Ϭ _T^(К) /m _T^(К)= =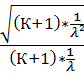

При увеличении порядка К-поток становится всё более регулярным.

Интервал времени между требованиями в потоке Эрланга К-го порядка подчинён закону распределения Эрланга К-го порядка как закон распределения суммы (К+1) независимых случайных величин с exp. Законом распределения

Ƒ_{к(t) =}

С параметрами:

m_к = (к+1)_* mₒ = (к+1)* - мат. ожидания

D_К = (К+1)* Dₒ = (К+1)* - дисперсия

где mₒ, Dₒ - параметры exp. Закона (Эрланг О порядка)

Кроме рассмотренных на практике имеют распространение:

Неординарные потоки (требования поступают не по одному, а группами)

Сложные детерминированные потоки – неслучайные по сути, но со сложной функцией моментов поступления.

Дискретные потоки – требования могут поступать только в определённые моменты времени (напр. на транспорте – по расписанию) и т.д.

Время обслуживания

Эффективность функционирования системы обслуживания, как уже говорилось ранее, определяется в частности временем обслуживания каждого требования. Длительность обслуживания в общем случае является случайной величиной, подчинённой некоторому закону распределения. В ТМО наиболее распространены следующие виды законов.

1. Показательное распределение длительности обслуживания

В этом случае время нахождения требования в канале обслуживания подчинено exp закону распределения с параметром М – среднее число заявок, обслуженных в канале за единицу времени (интенсивность обслуживания)

g(t) = t

Мат. ожидание и дисперсия времени обслуживания заявки в канале будут

m_(t) = ; D _(t) =

Показательное распределение времени обслуживания целесообразно применять в тех случаях, когда большее число требований требует для своего обслуживания сравнительно малого времени, а меньшее число требований – большого. (напр. на потоке – много мелких отправлений (заявок) – марки, конверты,…. реже заказные письма, телеграммы. Совсем редко отправление одним клиентом сразу большого числа.

Использование exp закона распределения времени обслуживания требований позволяет получить простые аналитические выражения для характеристик СМО.

2. Эрланговское распределение длительности обслуживания

Используется при анализе СМО в тех случаях, когда процесс обслуживания можно представить как К последовательных, независимых этапов, длительность обслуживания на каждом подчинена exp. Закону распределения с параметром . (распред. Эрланга (К-1)-го порядка)

3. Постоянная длительность обслуживания – применяется для приближённого расчёта СМО с сильной идеализацией процессов обслуживания.

Кр. этих законов распределения могут применяться и другие:

· с нестационарной интенсивностью обслуживания

· с нормально-распределением tобсл.

· с зависимостью tобсл. Сет типа требования и др.

В этих случаях получить аналитические выражения для анализа СМО часто не представляется возможным. Поэтому либо используют приближённые вычисления переходя к exp. законам с эквивалентными характеристиками по длительности обслуживания, либо используют имитационные модели.

Марковские случайные процессы.

Под случайным процессом понимают изменение во времени состояний некоторой физической системы заранее неизвестным случайным образом. При этом под физической системой будем понимать " техническое устройство, группу устройств, предприятие, отрасль, биологическую систему и т.д.

Случайный процесс протекающий в системе называется Марковским – если для " момента времени ,вероятностные характеристики процесса в будущем (t > ) зависят только от его состояния в данный момент времени

(в настоящем) и не зависят от того,когда и как система пришла в это состояние в прошлом.

(Например счетчик Гейгера,регистрирующий число космических частиц)

На практике Марковские процессы в чистом виде встречаются не часто. Однако нередко приходится иметь место с процессами, для которых влиянием предыстории можно пренебречь. Кроме того, если все параметры из «прошлого»,от которых зависит «будущее» включить в состоянии системы в «настоящем», то ее также можно рассматривать как Марковскую. Однако это приводит к значительному росту размерности??????? переменных и невозможности получить решение задачи.

В исследование операций большое значение занимают т.н. Марковские случайные процессы с дискретными состояниями и непрерывным временем.

Процесс называется процессом с дискретными состояниями, если все его возможные состояния , можно заранее?????? (перенумеровать). Переход системы из состояния в состояние переходит практически мгновенно –скачком.

Процесс называется процессом с непрерывным временем,если моменты перехода из состояния в состояние могут принимать " случайное значение на временной оси.

Например: Техническое устройство S состоит из двух узлов, каждый из которых в случайный момент времени может выйти из строя (отказать). После этого мгновенно начинается ремонт узла (восстановление),который продолжается случайное время.

Возможны следующие состояния системы:

- оба узла исправны;

- первый узел ремонтируется,второй исправен.

– второй узел ремонтируется,первый исправен

- оба узла ремонтируются.

Переход системы из состояния в состояние происходит в случайные моменты времени практически мгновенно.Состояния системы и связь между ними удобно отобразить с помощью графа состояний.

- состояния

 

- переходы

Переходы и отсутствуют т.к. отказы и восстановления элементов происходят независимо и случайно и вероятность одновременного выхода (восстановления) двух элементов бесконечно мала и?ей? можно пренебречь.

Если все потоки событий,переводящие систему S из состояния в состояние – простейшие, то процесс протекающий в такой системе будет Марковским. Это обуславливается тем, что простейший поток не обладает последействием, т.е. в нем «будущее» не зависит от «прошлого» и кр. того, он обладает? ординарности? – вероятность одновременного появления двух и более событий бесконечно мала – т.е невозможен переход из состояния в состояние, минуя несколько промежуточных состояний.

Для наглядности на графе состояний удобно у каждой стрелки перехода проставить интенсивность того потока событий, который переводит систему из состояния в состояние по данной стрелке ( -интенсивность потока событий,переводящего систему из состояния в .

 

такой граф называется размеченным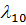

 

 

Используя размеченный граф состояний системы можно построить математическую модель данного процесса.

Обозначим (t)- вероятность i-ого состояния системы – вероятность того, что система в момент времени t находится в состоянии . Для " момента t справедливо? =1??

Пусть система в момент времени t находится в одном из состояний.

Определим вероятность того, что в момент времени t+∆ t система будет находится в состоянии . Это может быть в следующих случаях:

1) Система находилась в состоянии и за время ∆ t из него не вышла.

Это означает,что за время ∆ t не возникло события, переводящего систему в состояние (поток с интенсивностью ) или события,переводящего ее в состояние (поток с интенсивностью )

Можно показать,что вероятность этого будет равна (при малых ∆ t)

P( / )=1 – ( + )* ∆ t

При экспоненциальном законе распределения времени между двумя соседними требованиями?соответсвующем? простейшему потоку событий вероятность того, что на интервале времени ∆ t не возникнет ни одного требо вания в потоке с интенсивностью λ₁ будет равна

(см **)

Аналогично для потока с интенсивностью λ₂

Вероятность, что не возникнет ни одного требования

(см ***)

(2) Система находилась в состоянии S_i-1 и за время перешла в состояние S_i

(т.е. в потоке с интенсивностью возникло хотя бы одно событие) Вероятность этого равна для простейшего потока

**

Разлагая функцию f(t) в ряд Тейлора (t>0) получим (для t=∆ t)

f(∆ t)=f(0)+ (0)* ∆ t + *∆ + *∆ +…=

= +(-l) *∆ t+ +(∆ + +(∆ +…» 1-l*∆ t при ∆ t®0

***

(∆ t)/ ???????????= (∆ t/ * (∆ t/ =(1- *∆ t)(1- *∆ t)=

1- - *∆ t+ 1-( + )*∆ t+б.м при ∆ t®0

????????? l= +

(∆ t/l= + = 1-( + )*∆ t+б.м

 

(3) Система находилась в состоянии и за время ∆t перешла в состояние

Вероятность этого будет

Тогда вероятность, что система в момент времени t+∆t будет в состоянии S_i равна

Вычтем из обеих частей P_i(t), разделим на ∆t и перейдя к пределу при ∆t→0, получим

 

Подставив соответствующие значения интенсивностей переходов получим систему диф. уравнений, описывающих вероятности состояний системы как функции времени.(аргумент t-опустим).

 

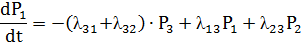
Данные уравнения называются уравнениями Колмогорова для дискретного Марковского процесса.

Задав начальные условия (напр. P₀(t=0)=1, P_i(t=0)=0 i≠0) и решив их, получим выражения для вероятности состояния системы как функции времени. Аналитические решения достаточно просто получить, если число уравнений ≤ 2,3. Если их больше, то обычно решают уравнения численно- на ЭВМ. (напр. м. Рунге-Кутта).

 

 

 

В теории случайных процессов доказано, что если число n состояний системы конечно и из каждого из них можно (за конечное число шагов) перейти в другое, то существует предел, к которому стремятся вероятности при t→ . Такие вероятности наз-ся Финальными вероятностями состояний, а установившийся режим- стационарным режимом функционирования системы.

Т.к. в стационарном режиме все , следовательно все =0

Приравняв в системе уравнений левые части 0 и, дополнив их уравнением

=1 получим систему линейных алгебраических уравнений, решив которую найдём значения Финальных вероятностей.

Пример Пусть в нашей системе интенсивности отказов и восстановления элементов следующие

Отказы 1эл:

2эл:

Ремонт 1эл:

2эл:

 

P₀+P₁+P₂+P₃=1

0=-(1+2)P₀+2P₁+3 P₂

0=-(2+2)P₁+1P₀+3P₃

0=-(1+3)P₂+2P₀+2P₃

0=-(2+3)P₃+2P₁+1P₂

 

 

Решив систему получим

P₀=6/15=0.4; P₁=3/15=0.2; P₂=4/15=0.27; P₃=2/15≈0.13

Т.е. в стационарном состоянии система в среднем

40% находится в состоянии S₀ (оба узла исправны),

20%- в состоянии S₁ (1-й эл-т ремонтируется, 2-й исправен),

27%- в состоянии S₂ (2-й эл-т………., 1…….),

13%- в состоянии S₃ – оба эл-та в ремонте.

 

Знание финальных вероятностей позволяет оценить среднюю эффективность работы системы и загрузку службы ремонта.

Пусть система в состоянии S₀ приносит доход 8 усл.ед. в единицу времени; в состоянии S₁-доход 3 усл.ед.; в состоянии S₂- доход 5;в состоянии S₃-доход=0

Стоимость ремонта в единицу времени для эл-та 1- 1(S_1,

12Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: