 |
Системы с ограниченным временем ожидания.
|
|
|
|
Пусть система имеет n каналов обслуживания. Входящий поток требований – простейшие с интенсивностью λ. Время обслуживания распределено по exp закону с параметром μ. Если в момент поступления требования все каналы заняты, то оно встает в очередь. Однако время пребывания требования вочереди – ограниченно. При этом максимальное время ожидания может быть детерминированным, так и случайным. По окончанию этого времени, если требование не поступило на обслуживания, то оно покидает систему не обcлуживаясь.
(1) Макс. Время ожидания T = const
В этом случае вероятность перехода системы из одного состояния в другое зависит не только от того, сколько требований находится в системе на обслуживании и в очереди (т.е. от состояния системы), но и от того как давно требование, стоящее в очереди, находится в системе. От этого зависит – будет ли требование оставаться в системе или покидает ее, т.к. время ожидания превысит допустимое т.е.????? последействие и последовательность состояний системы (процесс изменения состояний) – немарковская.
Поэтому для описания процесса функционирования такой СМО нельзя использовать уравнения размножения и гибели.
Для аналитического исследования СМО используется приближенное описание процессов их функционирования с помощью системы дифференциальных уравнений, за счет определённых допущений при увеличения мерности задачи при учете состояния каждого из каналов и т.д. |Бом.К.Лекц II|.
Кроме того для исследования подобных немарковских СМО (как впрочем и любых других, в том числе и марковских) широко используется имитационное моделирование. При этом оценки параметров исследуемой СМО ищутся на основе статистической обработки результатов моделирований, полученных по множеству прогонов (реализаций). Для этого используются как точечные, так и интервальные оценки позволяющие оценить точность полученных результатов.
|
|
|
Максимальная длительность ожидания ограниченна случайной величиной.
Ограничимся случаем, когда максимальная длительность ожидания требования в очереди T имеет exp. распределение.

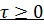 (функция распределения)
(функция распределения)
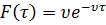 (функция плотности)
(функция плотности)
Здесь 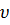 – параметр з-иа распределения. Среднее значение
– параметр з-иа распределения. Среднее значение 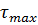 будет
будет 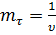
Такие процессы функционирования СМО можно представить следующим образом. (с.м. рис.)
На вход системы поступает поток требований (простейший) с интенсивностью  . Если не все каналы заняты (k < n), то пришедшие требования сразу же начинают обслуживаться. Обслуженные требования покидают систему с интенсивностью
. Если не все каналы заняты (k < n), то пришедшие требования сразу же начинают обслуживаться. Обслуженные требования покидают систему с интенсивностью 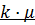 .
.
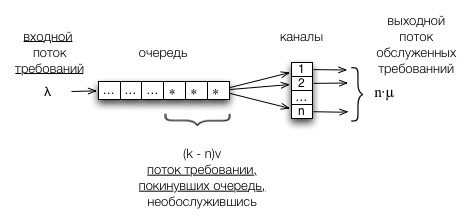
Если все каналы системы заняты, (k > n), то обслуженные требования покидают систему с интенсивностью 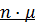 .
.
Кроме того, возникает еще один поток требований – покидающих систему не дождавшись обслуживания не дождавшись обслуживания. Интенсивность этого потока равна 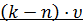 .
.
Т.к. показательное распределение макс. времени ожидания также обладает свойством «отсутствия памяти», т.е. распределение оставшегося времени ожидания не зависит от того, сколько времени требование уже прождало в очереди, то последовательность состояний системы оказывается «без последействия» и является «Марковской». Это позволяет описать ее с помощью уравнений «размножения и гибели». В частности для неограниченной очереди (m = ∞) они имеют вид:
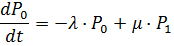
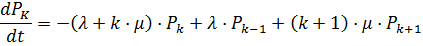
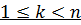
..

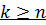
Значения финальных вероятностей соответственно равны:
Из 




Зная значения финальных вероятностей можно найти и составить характеристик функционирования СМО в стационарном режиме (m кан ; m оч ; m стат).
Замкнутая СМО
Наряду с задачами, когда интенсивность входного потока требований в систему λ неизменна, на практике, на практике часто встречаются задания, когда число источников требований ограничено, и интенсивность входного потока зависит от того, сколько источников уже послало требования в систему на обслуживание. В качестве примера рассмотрим следующую задачу.
|
|
|
n рабочих обслуживают R станков. Каждый станок может отказать в случайный момент времени. Время безотказной работы каждого станка подчинено exp. закону распределения
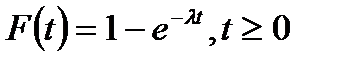
где t – момент наступления отказа
λ – параметр, который можно рассматривать как интенсивность потока отказов одного станка, если после отказа он мгновенно переводится в рабочее состояние. Однако при определении в стационарном режиме характеристик функционирования СМО необходимо иметь в виду, что не все требования, поступившие в систему, будут обслужены.
Поток этих требований с интенсивностью λсист=λPсист=λ(1-Рn+m) разобьётся на два потока:
обнаруживания с интенсивностью λобс= mканµ
покинувших систему из-за ограничения на время ожидания в очереди с интенсивностью
λпок = mочν
λсист=λобс + λпок
Тогда для любого требования на входе в систему из входного потока вероятности обслуживания или необнаруживания будут пропорциональны интенсивностям соответствующих потоков, т. е. 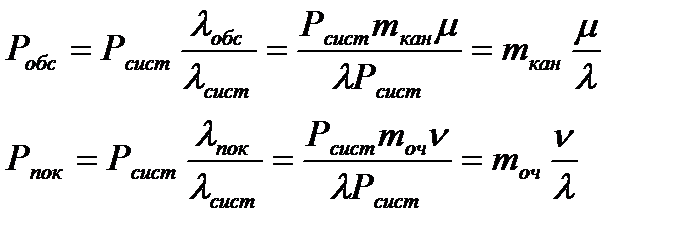
Средние временные характеристики на основании формул Литтла будут
1. Время нахождения в канале обслуживания 
2. Среднее время нахождения в очереди 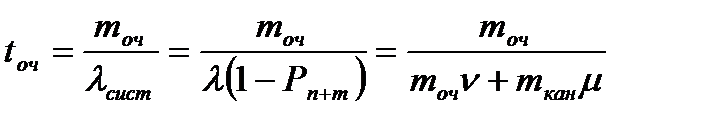
3. Среднее время нахождения в системе 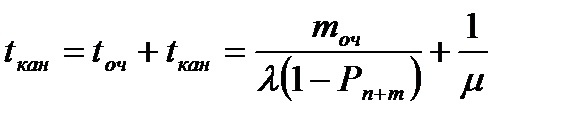
Если хотя бы один из рабочих свободен, то станок начинает обслуживаться. Время обслуживания распределено также экспоненциально с параметром µ. Если все рабочие заняты, то станок становится в очередь на обслуживание (ремонт), длина которой может быть не больше m = R-n.
Схематически данную систему, как СМО можно представить в следующем виде:
Заявки (R-k) каналы(n)
Очередь(k-n)
| m … 2 1 |
поток
(R-k)µnµ
Обозначим K – число заявок на обслуживание (число отказавших станков). Тогда интенсивность входного потока заявок зависит от числа отказавших станков и будет равна (R-k)λ. С учётом этого уравнения размножения и гибели, которыми можно описать СМО примут вид: при R > n
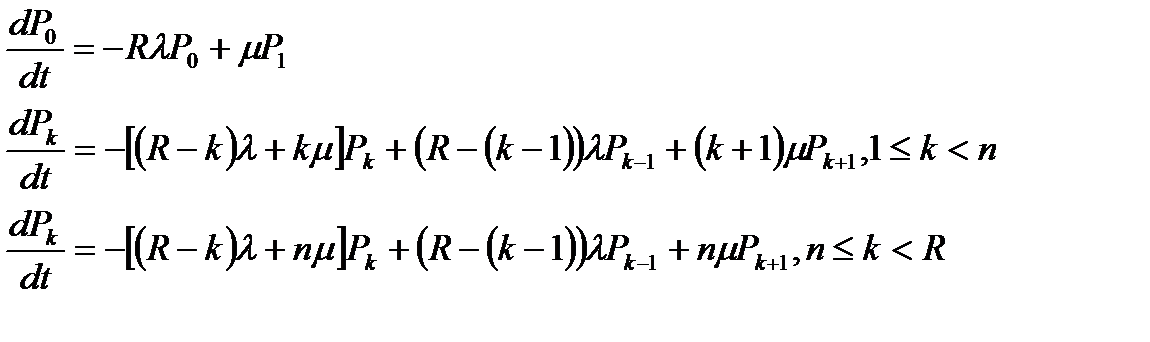
Т. к. общее число состояний системы конечно(0 ≤ k ≤ R), то при t  в системе существует режим статистического равновесия. Приравняв правые части уравнений модно найти финальный вероятности замкнутой системы
в системе существует режим статистического равновесия. Приравняв правые части уравнений модно найти финальный вероятности замкнутой системы
|
|
|
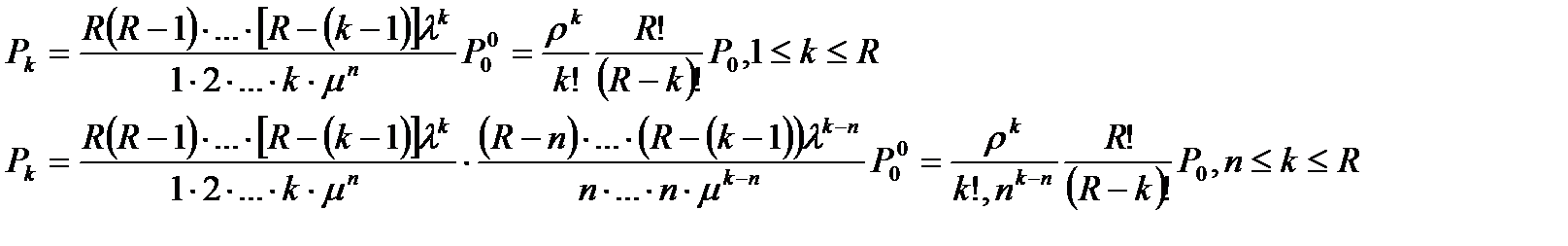

Зная значения финальных вероятностей можно найти все характеристик работы СМО в стационарном режиме.
Все рассматриваемые выше СМО мы анализировали в предположении, что все потоки событий, происходящих в системе – простейшие. Это позволяло описывать их достаточно просто с помощи уравнения Колмогорова и, в частности, уравнений размножения и гибели. Кроме того – получать достаточно простые выражения для финальных вероятностей состояний системы и её основные характеристик в режиме статистического равновесия.
В случаях, если эти допущения нарушаются, СМО нельзя рассмотреть как марновские и их аналитический анализ вызывает существенные трудности. Аналитические выражения для основных характеристик СМО удается получить только в отдельных случаях. Соответствующие выражения можно найти в литературе по ТМО.
В общем случае любые СМО можно исследовать с помощью имитационного моделирования (ниже и в л.р.).
Оптимизация параметров СМО.
При организации СМО важно выбрать ее параметры так, чтобы наилучшим образом решать стоящие перед ней задачи. При этом качество их решений определяется, как правило, с помощью векторного критерия эффективности, компонентами которого являются частные показатели эффективности СМО.
Решение задачи выбора рациональных параметров СМО как векторной – затруднительно. Поэтому на практике достаточно часто используют сведение частных показателей эффективности в один – обобщенный с помощью различных процедур свертки и далее задачу рассматривают как монокритериальную.
В качестве такого интегрального (обобщенного) показателя в широком классе задач можно использовать величину прибыли, получаемой от функционирования СМО, которая определяется, с одной стороны, доходами от обслуживания заявок (например, клиентов в парикмахерской), с другой стороны расходами на содержание системы (аренда помещений, зарплата работников и т.д.), штрафами за XXX XXX.
|
|
|
Оптимизируемыми параметрами при этом могут быть: число каналов обслуживания n, максимальная длина очереди m, интенсивность обслуживания 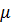 и др. характеристики СМО, которые варьируются в рамках заданных для них ограничений.
и др. характеристики СМО, которые варьируются в рамках заданных для них ограничений.
Однако стоимостной критерий не является универсальным. В ряде задач большее значение играет факт выполнение СМО поставленной перед ней задачей. Например, если в качестве СМО рассматривается система ПВО. Тогда в качестве показателя эффективности такой системы можно рассматривать м.о. числа обслуженных (пораженных) самолетов противника, вероятность проникновения самолета через систему ПВО (вероятность, что заявка не будет обслужена) и др.
(Примеры СМО смотри л.р. по курсу ИО М.-1992)
Самостоятельно на РГР
X(t) – число требований, поступивших в систему к моменту t.
Y(t) – число требований, покинувших систему к моменту t.
Z= X(t) - Y(t) – число требований, находящихся в системе в момент t.
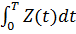 – общее время, затраченное всеми требованиями на нахождение в системе за время T.
– общее время, затраченное всеми требованиями на нахождение в системе за время T.
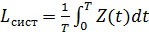 – среднее число требований в системе в момент t.
– среднее число требований в системе в момент t.

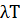 – средняя вероятность поступлений в систему за время Т
– средняя вероятность поступлений в систему за время Т
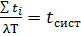 – средне время нахождения в системе
– средне время нахождения в системе
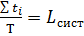 =>
=> 
(здесь 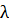 – интенсивность поступления требований в систему =
– интенсивность поступления требований в систему =  )
)
| Сист. |



но  отсюда
отсюда 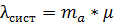
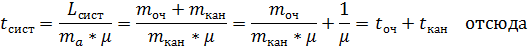
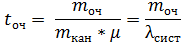
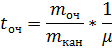
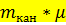 – среднее число требований, освободившихся из каналов за единицу времени.
– среднее число требований, освободившихся из каналов за единицу времени.
Далее страница 59 совершено нечитаемая
|
|
|


