Математическая модель принятия решения

Математическая модель принятия решения представляет собой формализацию той схемы, которая приведена в системном описании ЗПР. Для построения математической модели принятия решения необходимо задать следующие три множества: - множество допустимых альтернатив,

У - множество возможных состояний среды,

А - множество возможных исходов.

(Всегда предполагается, что множество X содержит не менее двух альтернатив - иначе надобность в принятии решения отпадает.)

В системном описании ЗПР альтернативы интерпретируются как управляющие воздействия, а исходы - как состояния управляемой подсистемы.

Так как состояние управляемой подсистемы полностью определяется выбором управляющего воздействия и состоянием среды, то каждой паре (х, у), где х 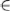 X и у 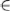 У, соответствует определенный исход а 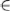А. Другими словами, существует функция F:

X × У 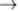 А, которая называется функцией реализации. Функция реализации каждой паре вида (альтернатива, состояние среды) ставит в соответствие определяемый ею исход.

Набор объектов (X, У, А, F) составляет реализационную структуру задачи принятия решения. Реализационная структура отражает связь между выбираемыми альтернативами и исходами; в общем случае эта связь не является детерминированной (однозначной): появление того или иного конкретного исхода зависит не только от выбранной альтернативы, но и от наличного состояния среды. Таким образом, имеется, как принято говорить, неопределенность стратегического типа; эта неопределенность создается за счет воздействия среды на объект управления.

В зависимости от информации, которую имеет при принятии решения управляющая подсистема относительно состояния среды, различают несколько основных типов задач принятия решения.

•   Принятие решения в условиях определенности характеризуется тем, что состояние среды является фиксированным (неизменным), причем управляющая система «знает», в каком состоянии находится среда.

•   Принятие решения в условиях риска означает, что управляющая подсистема имеет информацию стохастического характера о поведении среды (например, ей известно распределение вероятностей на множестве состояний среды).

•   Принятие решения происходит в условиях неопределенности, если никакой дополнительной информации (кроме знания самого множества возможных состояний среды) управляющая подсистема не имеет.

•   Принятие решения в теоретико-игровых условиях имеет место тогда, когда среду можно трактовать как одну или несколько целенаправленных управляющих подсистем. В этом случае математическая модель принятия решения называется теоретико-игровой моделью (игрой).

Реализационная структура задачи принятия решения составляет ее первую компоненту. Вторая компонента ЗПР называется ее оценочного структурой. Если реализационная структура определяет возникающий результат, то оценочная структура указывает оценку этого результата с точки зрения принимающего решение.

В математической модели ЗПР оценочная структура может задаваться различными способами.

Например, если принимающий решение может оценить эффективность (равнозначные по смыслу термины: «полезность», «ценность») каждого исхода а 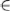  А некоторым числом φ(а), то оценочная структура задается в виде пары (А, φ), где φ: А  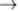R; при этом φ называется оценочной функцией.

Например, в задачах юриспруденции, φ(а) - количество правонарушителей на 1000 жителей. Для построения оценочной функции необходим некоторый измеримый критерий эффективности исходов. В большинстве практических задач принятия решения исходы (в качестве которых выступают реальные объекты и явления) оцениваются, как правило, не по одному, а по нескольким критериям.