Математическая модель задачи принятия решения при многих критериях

Математическая модель задачи принятия решения при многих критериях может быть представлена в виде (D; f₁…f_m), где D - некоторое множество (множество допустимых исходов), f_j - числовая функция, заданная на множестве D; при этом f_j(a) есть оценка исхода а 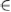 D по j-му критерию j=().Такая модель соответствует задаче принятия решения в условиях определенности, в которой множество альтернатив отождествляется с множеством допустимых исходов, а оценочная структура задается вектором (f₁…f_m).

Критерий f_j называется позитивным, если принимающий решение стремится к его увеличению, и негативным, если он стремится к его уменьшению.

В конкретных задачах принятия решений характер критерия устанавливается по содержательным соображениям. Технически «превращение» негативного критерия в позитивный (и наоборот) можно осуществить заменой знака; при рассмотрении многокритериальных ЗПР в общем виде предполагается, если не оговорено противное, что все имеющиеся критерии являются позитивными. В многокритериальной ЗПР с позитивными критериями цель принимающего решение - получение исхода, имеющего как можно более высокие оценки по каждому критерию.

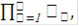Пусть Y_j - множество значений функции f_j, т.е. множество всех оценок по j-му критерию (j = ).Тогда множествоY= состоящее из всевозможных упорядоченных наборов оценок по критериям 1,…, m, называется множеством векторных оценок. Любой элемент у  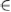У представляет собой вектор у = (y₁,…, y_m ), где y _j 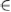Y_j. Для всякого исхода а  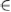D набор его оценок по всем критериям, т.е. набор (f ₁ (а),…, f_m(а)) есть векторная оценка исхода а. В рамках модели векторная оценка исхода содержит полную информацию о ценности (полезности) этого исхода для принимающего решение, и сравнение любых двух исходов заменяется сравнением их векторных оценок.

Другой способ задания оценочной структуры со стоит в указании отношения предпочтения исходов, что сводится к перечислению пар исходов (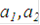), для которых  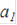лучше, чем  (это записывается в виде 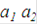 и читается « 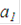предпочтительней, чем ).

Наиболее распространенным является задание оценочной структуры в виде оценочной функции φ.

Целевая функция f есть композиция функции реализации F и оценочной функции φ т.е. f = φ ° F. Таким образом, f (x, y) = φ (F (x, у)). Целевая функция имеет следующий содержательный смысл: число f (x, y) есть оценка полезности (с точки зрения принимающего решение) того исхода, который возникает в ситуации, когда он выбирает альтернативу х, а среда принимает состояние у.

Оптимальность по Парето - такое состояние системы, при котором значение каждого частного показателя, характеризующего систему, не может быть улучшено без ухудшения других.

Парето-оптимальность исхода а* означает, что он не может быть улучшен ни по одному из критериев без ухудшения по какому-нибудь другому критерию.

Для наглядного представления доминирования по Парето и Парето - оптимальности рассмотрим случай двух позитивных критериев f₁ и f_2.

Векторные оценки исходов представим точками координатной плоскости (по оси абсцисс откладываем значения критерия f₁, а по оси ординат - значения критерия f₂).

В случае, когда множество допустимых исходов является дискретным (конечным), получаем «картинку» типа

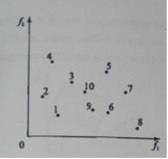
Здесь Парето-оптимальными являются исходы {4, 5, 7, 8}. При этом каждый исход, не являющийся Парето-оптимальным, доминируется по Парето некоторым Парето-оптимальным исходом (не обязательно одним).

В случае, когда множество допустимых исходов является непрерывным, их векторные оценки «заполняют» некоторую область Q не плоскости и получается «картинка» вроде

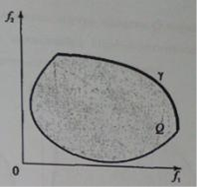
В этом случае множество Парето - оптимальных исходов (жирная линия Y) представляет собой часть границы Q, её «северо-восточную» границу. Здесь так же любой исход, не являющийся Парето - оптимальным, доминируется по Парето-оптимальным исходам.