 |
Теорема 1. Критерий собственных чисел (для матриц).
|
|
|
|
Характеристический многочлен матрицы.
Определение 1. Пусть 
- квадратная матрица порядка 
, элементы которой вещественные или комплексные числа.
Характеристическим многочленом матрицы 
называют многочлен, равный определителю матрицы 
. Этот многочлен будем обозначать так: 
, т.е. 
или
Как следует из определения определителя - го порядка, степень характеристического многочлена квадратной матрицы равна её порядку. Следовательно, характеристический многочлен матрицы имеет вид: 
. Произведение 
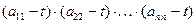является
единственным из ! слагаемых определителя матрицы , содержащим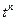 
и 
. Следовательно, 
. Сумму 
называют следом матрицы и обозначают так: 
. Таким образом, 
. Положим 
. Тогда 
.
Существуют формулы, выражающие и остальные коэффициенты характеристического многочлена через элементы матрицы .
Пример 1. Найдём характеристический многочлен матрицы 
.
Воспользуемся определением: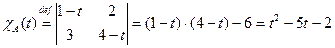 
. Результат вычисления согласуется с формулами, полученными для коэффициентов характеристического многочлена:
.
Определение 2. Пусть - квадратная матрица порядка , элементы которой вещественные или комплексные числа, 
- многочлен с вещественными или комплексными коэффициентами.
Значением многочлена 
от матрицы называют матрицу, обозначаемую 
и такую, что
, где 
- единичная матрица порядка .
Пример 2. Найдём значениемногочлена от матрицы из примера 1.
Итак, 
. Это равенство верно и для любой квадратной матрицы. Это утверждение, называемое теоремой Гамильтона-Кэли, приведём без доказательства.
Теорема 1. (Гамильтона-Кэли для матриц).
Значением характеристического многочлена от квадратной матрицы является нулевая матрица, т.е.
|
|
|
.
Определение 3. Пусть и 
- квадратные матрицы порядка , элементами которых являются вещественные или комплексные числа.
Будем говорить, что матрица подобна матрице (обозначение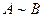 
), если существует такая неособенная матрица 
порядка , что справедливо равенство 
Лемма 1. Отношение подобия является отношением эквивалентности, т.е. это отношение обладает тремя свойствами:
1. 
(рефлексивность).
2. Если 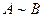, то и 
(симметричность).
3. Если 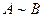и 
, то 
(транзитивность).
Доказательство. 1. 
.
2. Если , то 
, и .
3. Если и 
, то 
.
Лемма 2. Характеристические многочлены подобных матриц равны, т.е. если 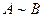, то 
.
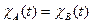Доказательство. Пусть 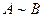, т.е. . Отсюда следует: 
Замечание. Может оказаться, что 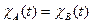, но матрицы и не являются подобными.
Например, если 
, а матрица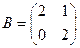 
, то 
. Однако, матрицы и не являются подобными. Если , то 
т.к. 
. Однако 
.
Собственные числа и собственные векторы матрицы.
Определение 1. Пусть - квадратная матрица порядка , элементы которой вещественные (или комплексные) числа. Число 
будем называть собственным числом матрицы , если найдётся такой ненулевой вещественный (или комплексный) столбец 
высоты , для которого выполняется равенство
.
В этом случае столбец называют собственным вектором матрицы , соответствующим собственному числу .
Замечание. Собственные числа называют также собственными значениями или характеристическими числами матрицы . Собственные векторы называют также собственными столбцами матрицы
Теорема 1. Критерий собственных чисел (для матриц).
Для того чтобы число 
K было собственным числом матрицы 
(K), необходимо и достаточно, чтобы это число было корнем характеристического многочлена этой матрицы, т.е.
( - собственное число матрицы ) 
.
Доказательство. Из определения 1 следует, что число является собственным числом матрицы тогда и только тогда, когда найдётся такой ненулевой столбец высоты с элементами из K, для которого выполняется равенство . Последнее равенство, очевидно, эквивалентно следующему: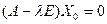 
. Таким образом, это утверждение равносильно тому, что система линейных алгебраических уравнений 
имеет ненулевое решение . По теореме 2 §1главы IY
|
|
|
это возможно тогда и только тогда, когда определитель этой системы равен нулю, т.е. 
, а это и означает, что 
. Таким образом число - корень характеристического многочлена матрицы .
Это доказательство можно записать с помощью символов:
( -собственное число матрицы ) 
K 
, 
, т.ч. 
) 
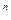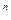K , , т.ч. 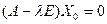) ( имеет ненулевое решение)
корень характеристического многочлена матрицы ).
Определение 2. Совокупность всех собственных чисел матрицы (K) с учётом их кратности как корня характеристического многочлена, будем называть спектром матрицы , и обозначать так: 
.
Пример 1. Найдём собственные числа, собственные векторы и спектр матрицы 
.
Найдём характеристический многочлен этой матрицы: 
Следовательно, нашли спектр матрицы : 
.
Теперь найдём собственные векторы этой матрицы.
1) Сначала найдём собственные векторы, соответствующие собственному числу 
.
Для этого нужно найти ненулевые решения системы линейных алгебраических уравнений 
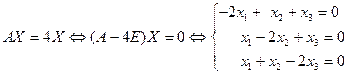(1).
Решим систему (1) методом Гаусса в матричной форме:
Следовательно, система (1) равносильна системе 
.
Положим 
. Тогда: 
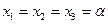. Таким образом, собственный вектор матрицы , соответствующий собственному числу , имеет вид: 
, где 
.
2) Теперь найдём собственные векторы, соответствующие собственному числу 
.
Для этого нужно найти ненулевые решения системы линейных алгебраических уравнений
(2).
Положим 
. Тогда 
. Таким образом, собственный вектор матрицы , соответствующий собственному числу , имеет вид: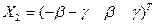 
, где числа 
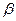и 
не равны нулю одновременно.
Лемма. Ненулевая линейная комбинация собственных векторов матрицы , соответствующих одному и тому же собственному числу , является собственным вектором этой матрицы, соответствующим этому собственному числу.
Доказательство. Пусть 
- собственные векторы матрицы (K), соответствующие одному и тому же собственному числу K, т.е.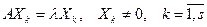 
. Пусть 
K и пусть 
. Тогда отсюда следует, что 
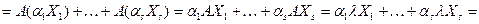
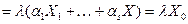, причём . Следовательно, 
является собственным вектором матрицы , соответствующим собственному числу .
|
|
|
Без доказательства приведём формулировку основной теоремы высшей алгебры.
|
|
|
