 |
Теорема 2. (Основная теорема высшей алгебры.)
|
|
|
|
Для любого многочлена с комплексными коэффициентами степени большей или равной единицы (т.е. отличного от постоянной) найдётся по крайней мере один комплексный корень, т.е. если  C для
C для  ,
,  , то существует такое комплексное число
, то существует такое комплексное число  C, что
C, что 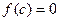 .
.
Следствие. Любой многочлен  с комплексными коэффициентами степени большей или равной единицы может быть записан следующим образом:
с комплексными коэффициентами степени большей или равной единицы может быть записан следующим образом:  , где
, где  - старший коэффициент,
- старший коэффициент,  - степень этого многочлена,
- степень этого многочлена, 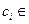 C для
C для  .
.
Теорема 3. Для любой квадратной матрицы с комплексными элементами найдётся по крайней мере один собственный вектор.
Доказательство. Пусть  (C). Тогда
(C). Тогда  - многочлен с комплексными коэффициентами, степень которого равна натуральному числу
- многочлен с комплексными коэффициентами, степень которого равна натуральному числу  . По основной теореме высшей алгебре у этого многочлена существует по крайней мере один корень
. По основной теореме высшей алгебре у этого многочлена существует по крайней мере один корень  , который по теореме 1 является собственным числом матрицы
, который по теореме 1 является собственным числом матрицы  . Из определения 1 следует, что найдётся такой ненулевой комплексный столбец
. Из определения 1 следует, что найдётся такой ненулевой комплексный столбец  высоты
высоты  , для которого выполняется равенство
, для которого выполняется равенство  , т.е.
, т.е.  - собственный вектор матрицы
- собственный вектор матрицы  , соответствующим собственному числу
, соответствующим собственному числу  .
.
Теорема 4. Все собственные числа вещественной симметричной матрицы являются вещественными числами, т.е. если 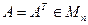 (C), то
(C), то  , где
, где  R,
R,
 .
.
Доказательство. Как следует из определения 1§4, степень характеристического многочлена  равна порядку матрицы
равна порядку матрицы  , т.е.
, т.е.  . Из следствия к основной теореме высшей алгебры получаем:
. Из следствия к основной теореме высшей алгебры получаем:
 , где
, где  C для
C для  . Покажем, что
. Покажем, что  R для
R для  .
.
Напомним, что любое комплексное число, в частности  , может быть записано в алгебраической форме:
, может быть записано в алгебраической форме:  , где
, где  R, а
R, а  -мнимая единица. Тогда число
-мнимая единица. Тогда число  является комплексно сопряжённым с
является комплексно сопряжённым с  . Если
. Если  , то
, то 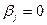 и
и  R.
R.
Фиксируем  такое, что
такое, что  . Из теоремы 1 следует, что
. Из теоремы 1 следует, что  - собственное число матрицы
- собственное число матрицы  , т.к. является корнем её характеристического многочлена. Следовательно, по определению 1 существует собственный вектор
, т.к. является корнем её характеристического многочлена. Следовательно, по определению 1 существует собственный вектор  C
C 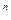 матрицы
матрицы  , соответствующий собственному числу
, соответствующий собственному числу  , т.е.
, т.е.  , причём
, причём  . Пусть
. Пусть  . Теперь подсчитаем двумя способами число
. Теперь подсчитаем двумя способами число  :
:
|
|
|
1) 
 , где
, где 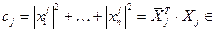 R,
R, 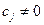 , т.к.
, т.к. 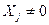 .
.
2) 
 . Здесь
. Здесь  , т.к.
, т.к.  - вещественная симметричная матрица.
- вещественная симметричная матрица.
Итак,  . Следовательно,
. Следовательно,  , откуда получаем,
, откуда получаем,  , т.к.
, т.к. 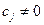 .
.
Таким образом,  R, и теорема доказана.
R, и теорема доказана.
Замечание. Поясним обозначения, использованные в доказательстве теоремы. Если  , то
, то
 - это матрица того же строения с элементами
- это матрица того же строения с элементами  . Здесь черта обозначает операцию комплексного сопряжения.
. Здесь черта обозначает операцию комплексного сопряжения.
Кроме того, в доказательстве использовано утверждение, которое легко доказать самостоятельно, а именно:
если  и
и  две матрицы с комплексными элементами, для которых определено произведение
две матрицы с комплексными элементами, для которых определено произведение 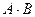 , то
, то  .
.
Следствие. Для любого собственного числа вещественной симметричной матрицы существует вещественный собственный вектор, соответствующий этому собственному числу.
Доказательство. Действительно, в этом случае собственный вектор является решением системы линейных алгебраических уравнений с вещественными коэффициентами.
Определение 3. Два вещественных столбца  и
и  одинаковой высоты будем называть ортогональными, если сумма произведений их соответствующих элементов равна нулю. Обозначение:
одинаковой высоты будем называть ортогональными, если сумма произведений их соответствующих элементов равна нулю. Обозначение:  , т.е.
, т.е.
 .
.
Два вещественные строки 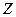 и
и  одинаковой длины будем называть ортогональными, если сумма произведений их соответствующих элементов равна нулю. Обозначение:
одинаковой длины будем называть ортогональными, если сумма произведений их соответствующих элементов равна нулю. Обозначение:  , т.е.
, т.е.
 .
.
Пример 2. Столбцы 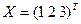 и
и  ортогональны, т.к.
ортогональны, т.к.  .
.
Строки  и
и  ортогональны, т.к.
ортогональны, т.к. 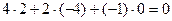 .
.
Теорема 5. Собственные векторы вещественной симметричной матрицы, соответствующие различным собственным числам, ортогональны.
Доказательство. Пусть  - вещественная симметричная матрица,
- вещественная симметричная матрица,  - её собственные числа, причём
- её собственные числа, причём  . Столбцы
. Столбцы  и
и  - собственные векторы матрицы
- собственные векторы матрицы  , соответствующие собственным числам
, соответствующие собственным числам  и
и  . Следовательно,
. Следовательно, 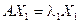 и
и  , причём
, причём 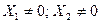 . Мы хотим доказать, что
. Мы хотим доказать, что  .
.
|
|
|
Подсчитаем двумя способами число 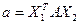 :
:
1) 
2) 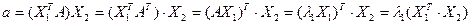
Итак,  , причём
, причём  . Следовательно,
. Следовательно,  и
и  .
.
Пример 3. В примере 1 было показано, что любой собственный вектор матрицы  , соответствующий собственному числу
, соответствующий собственному числу  , имеет вид
, имеет вид  , где
, где  .
.
Любой собственный вектор той же матрицы, соответствующий собственному числу  , имеет вид
, имеет вид
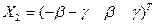 , где числа
, где числа 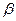 и
и  не равны нулю одновременно.
не равны нулю одновременно.
Подсчитаем число 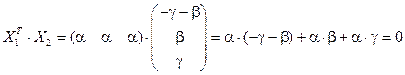 . Следовательно, результат вычисления согласуется с теоремой 5, и
. Следовательно, результат вычисления согласуется с теоремой 5, и  .
.
|
|
|


