 |
Построение фундаментальной системы решений
|
|
|
|
Положим 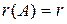 . Пусть общее решение системы (2) записано в виде
. Пусть общее решение системы (2) записано в виде
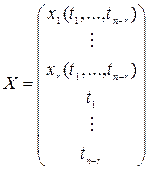 ,
,
где  ,…,
,…, 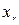 – главные (базисные) переменные,
– главные (базисные) переменные,  ,…,
,…,  – значения свободных переменных
– значения свободных переменных  ,…,
,…, 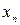 . Выберем
. Выберем 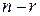 решений системы (2), полученных из общего решения следующим образом: одно из значений свободных переменных полагается равным 1, а остальные – равными 0:
решений системы (2), полученных из общего решения следующим образом: одно из значений свободных переменных полагается равным 1, а остальные – равными 0:
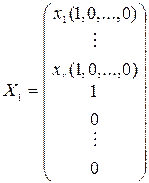 ,
, 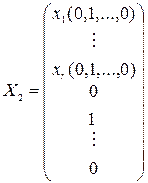 , …,
, …, 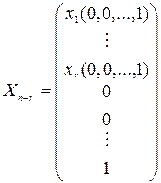 .
.
Эти решения образуют нормальную фундаментальную систему решений однородной системы (2). Они обладают следующим свойством:
Любое решение  системы (2) может быть единственным образом представлено в виде:
системы (2) может быть единственным образом представлено в виде:
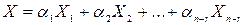 ,
,
где 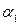 ,…,
,…, 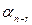 – некоторые числа.
– некоторые числа.
Любой набор из  решений системы (2), обладающий указанным свойством, называется фундаментальной системой решений системы (2).
решений системы (2), обладающий указанным свойством, называется фундаментальной системой решений системы (2).
Задания
Задание 1. Решить однородную систему линейных алгебраических уравнений. Указать общее решение системы и фундаментальный набор решений.
1.1. 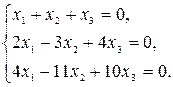
1.2. 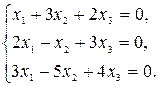
1.3. 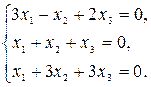
1.4. 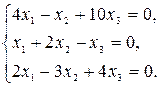
1.5. 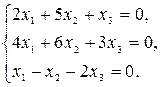
1.6. 
1.7. 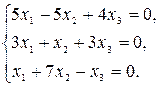
1.8. 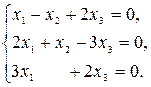
1.9. 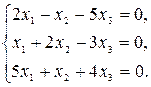
1.10. 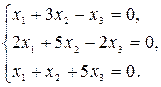
Задание 2. Найти фундаментальныйнабор решений однородной системы линейных уравнений.
2.1. 
2.2. 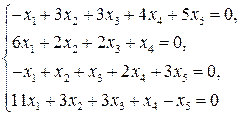
2.3. 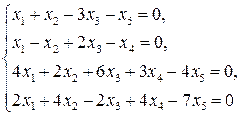
2.4. 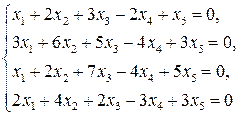
2.5. 
2.6. 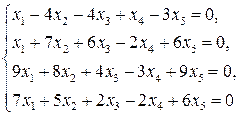
2.7. 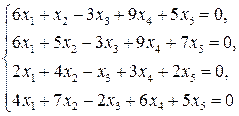
2.8. 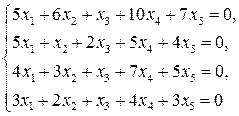
2.9. 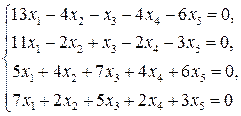
2.10. 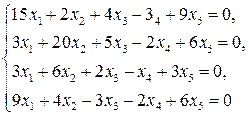
Задание 3. Найти общее решение системы линейных уравнений методом Гаусса, выделив базисные неизвестные, и одно частное решение.
3.1. 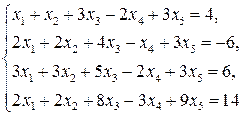
3.2. 
3.3. 
3.4. 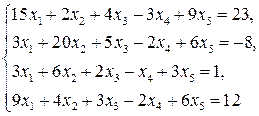
3.5. 
3.6. 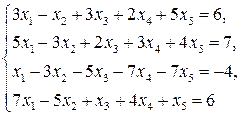
3.7. 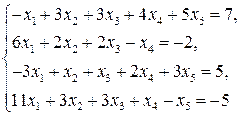
3.8. 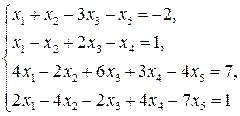
3.9. 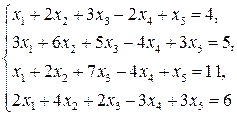
3.10. 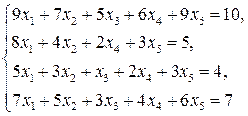
Методика и порядок выполнения работы
Пример 1
Решить однородную систему линейных алгебраических уравнений. Указать общее решение системы и фундаментальный набор решений.

Решение
|
|


|
|




 ~
~ 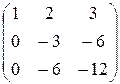 ~
~ 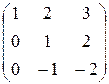 ~
~  .
.
Из последней ступенчатой системы видно, что ранг матрицы системы равен 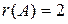 , а количество переменных равно
, а количество переменных равно  , так как
, так как  , то система неопределенна.
, то система неопределенна.
|
|
|
Количество базисных переменных равно 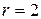 . В качестве главных переменных можно выбрать
. В качестве главных переменных можно выбрать  и
и  , соответствующие столбцам ненулевого минора второго порядка:
, соответствующие столбцам ненулевого минора второго порядка: 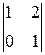 , в качестве свободной переменной –
, в качестве свободной переменной – 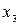 .
.
Запишем систему, соответствующую полученной матрице:
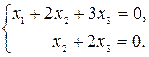
Из второго уравнения выражаем  через
через 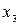 , получим:
, получим: 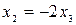 . Подставляя это выражение в первое уравнение, получим:
. Подставляя это выражение в первое уравнение, получим: 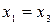 . Обозначив
. Обозначив  , получим общее решение системы
, получим общее решение системы  . это решение можно записать в виде:
. это решение можно записать в виде:  . Фундаментальную систему решений образует решение
. Фундаментальную систему решений образует решение 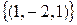 .
.
Пример 2
Найти фундаментальныйнабор решений однородной системы линейных уравнений.
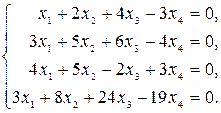
Решение
|


|
|


|

|
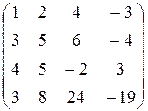 ~
~ 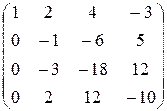 ~
~
|



|
|
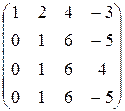 ~
~ 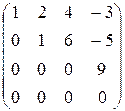 .
.
Из последней ступенчатой системы видно, что ранг матрицы системы равен 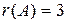 , а количество переменных равно
, а количество переменных равно 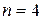 , так как
, так как  , то система неопределенна.
, то система неопределенна.
Количество базисных переменных равно  . В качестве главных переменных можно выбрать
. В качестве главных переменных можно выбрать 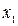 ,
,  и
и  , соответствующие столбцам ненулевого минора третьего порядка:
, соответствующие столбцам ненулевого минора третьего порядка: 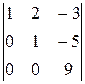 , в качестве свободной переменной –
, в качестве свободной переменной – 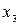 .
.
Запишем систему, соответствующую полученной матрице:
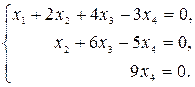
Из третьего уравнения получим: 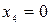 . Подставляя это выражение в первое и второе уравнения, получим:
. Подставляя это выражение в первое и второе уравнения, получим: 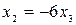 ,
, 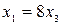 . Обозначив
. Обозначив  , получим общее решение системы
, получим общее решение системы 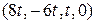 . это решение можно записать в виде:
. это решение можно записать в виде: 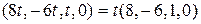 . Фундаментальную систему решений образует решение
. Фундаментальную систему решений образует решение  .
.
Пример 3
Найти общее решение системы линейных уравнений методом Гаусса, выделив базисные неизвестные, и одно частное решение.

Решение
Проведем элементарные преобразование расширенной матрицы системы по методу Гаусса:
|
|
|






|

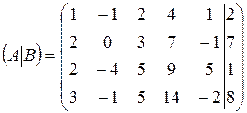
|
|
|



 ~
~  ~
~  ~
~
~ 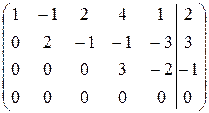 .
.
Из последней ступенчатой системы видно, что ранг матрицы системы равен 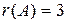 , ранг расширенной матрицы равен
, ранг расширенной матрицы равен 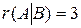 , а количество переменных равно
, а количество переменных равно 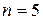 , так как
, так как 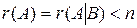 , то система совместна и неопределенна.
, то система совместна и неопределенна.
|
|
|
Количество базисных переменных равно  . В качестве главных переменных можно выбрать
. В качестве главных переменных можно выбрать  ,
,  и
и  , соответствующие столбцам ненулевого минора третьего порядка:
, соответствующие столбцам ненулевого минора третьего порядка: 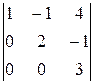 , в качестве свободных переменных –
, в качестве свободных переменных – 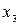 и
и 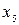 .
.
Запишем систему, соответствующую полученной матрице:
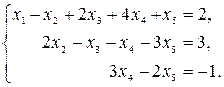
Из третьего уравнения выражаем  через
через 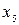 , получим:
, получим: 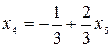 . Подставляя это выражение во второе уравнение, получим:
. Подставляя это выражение во второе уравнение, получим:  . Подставляя выражения для
. Подставляя выражения для  и
и  в первое уравнение, получим:
в первое уравнение, получим: 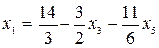 . Обозначив
. Обозначив 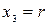 , а
, а  получим общее решение системы
получим общее решение системы
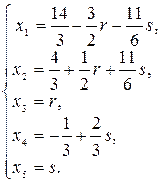
Придавая свободным переменным любые значения, будем получать частные решения системы. Частным решением системы будет являться решение 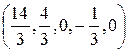 .
.
Вопросы для защиты работы
1. Однородные и неоднородные системы.
2. Совместные и несовместные системы.
3. Что называется решением системы?
4. Сформулировать теорему Кронекера-Капелли.
5. Что означает «исследовать систему уравнений»?
6. Что можно сказать о множестве решений системы линейных уравнений, если ранг 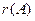 матрицы этой системы и ранг
матрицы этой системы и ранг 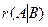 расширенной матрицы равны нулю?
расширенной матрицы равны нулю?
7. Фундаментальная система решений?
|
|
|


