2.3. Измерение частоты осциллографом с синусоидальной разверткой (метод фигур Лиссажу)

2. 3. Измерение частоты осциллографом с синусоидальной разверткой (метод фигур Лиссажу)

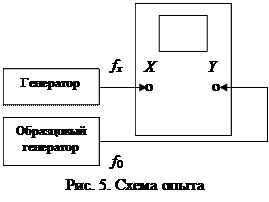
Метод фигур Лиссажу основан на сравнении частоты двух гармонических сигналов, т. е. сигнал, частота которого измеряется, должен быть синусоидальной формы. Собственная развертка осциллографа отключается. На вход X осциллографа подается исследуемый сигнал с частотой f_x, а на вход Y – гармонический сигнал с образцовой частотой f₀. Частоту образцового генератора подстраивают так, чтобы на экране осциллографа получилось устойчивое изображение одной из фигур, приведенных в табл. 1.

 

Таблица 1

 

Соотношение частот	Фазовый сдвиг, град

 

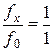
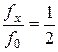
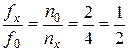Соотношение частот двух гармонических колебаний может быть определено как отношение числа точек пересечения с вертикальной прямой к числу точек пересечения с горизонтальной прямой. Например, как показано на рис. 4, указанное выше соотношение составляет: . Прием, когда на вход Х осциллографа подается гармонический сигнал, называют синусоидальной разверткой.

Соберите схему (рис. 5). Получите устойчивое изображение одной из фигур Лиссажу, срисуйте его. Определите частоту f_x и вычислите погрешность измерения. Увеличьте частоту f₀ в два или три раза, наблюдайте и зарисуйте соответствующую фигуру Лиссажу.

 

 

3. Измерение частоты при помощи цифрового электронно-счетного частотомера

 

Подайте прямоугольные импульсы от генератора на частотомер (рис. 6). Задайте произвольную частоту сигнала, измерьте его период и частоту при различных значениях времени счета. Определите погрешность встроенного частотомера генератора.

 

4. Измерение фазового сдвига при помощи осциллографа

 

Фаза является одним из основных параметров, определяющих состояние колебательного процесса в данный момент времени. Для гармонического колебания 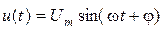 с амплитудой U_m и круговой частотой w текущее (мгновенное) значение фазы в момент t следующее: j(t) =   = wt + j, где j – начальная фаза. Таким образом, фаза – это аргумент синусоидальной функции, линейно зависящий от времени.

Фазовым сдвигом Dj двух гармонических сигналов одинаковой частоты называется модуль разности их начальных фаз: Dj = |j₁ – j₂|. Фазовый сдвиг связан со сдвигом сигналов во времени (рис. 7) и может быть выражен в радианах или градусах.

 

Рис. 7. Иллюстрация фазового сдвига

 

Обозначив через t₁ и t₂ моменты времени, когда напряжения U₁ и U₂ имеют одинаковую фазу, получим

 

wt₁ + j₁ = wt₂ + j₂,

 

отсюда

Dj = j₁ – j₂ = w(t₂ – t₁) = 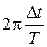[рад],

 

где Т – период колебаний; Dt – сдвиг сигналов во времени.

То же самое в градусах:

 

 

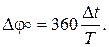
4. 1. Способ линейной развертки

Способ линейной развертки заключается в том, что напряжения u₁(t) и u₂(t) подаются на входы вертикального отклонения двулучевого или двухканального осциллографа. При этом осциллограмма будет иметь вид, представленный на рис. 7. Фазовый сдвиг вычисляется по формуле

 

,

 

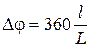где l и L – измеренные на осциллограмме длины отрезков, соответствующие Dt  и Т.

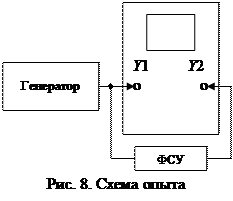Соберите схему (рис. 8). Настройте осциллограф для работы в двухканальном режиме. На вход первого канала Y1 подается сигнал с частотой 400 Гц от генератора, а на вход второго канала Y2 – тот же сигнал, прошедший через фазосдвигающее устройство (ФСУ). Наблюдайте изменение осциллограммы при вращении вала ФСУ. Зарисуйте осциллограмму при одном из положений вала ФСУ. Определите сдвиг фаз.

 

⇐ Предыдущая45678910111213Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: