 |
4. Измерение оптических параметров твердых тел
|
|
|
|
4. ИЗМЕРЕНИЕ ОПТИЧЕСКИХ ПАРАМЕТРОВ ТВЕРДЫХ ТЕЛ
Электромагнитное (световое) поле в веществе описывается векторами напряженности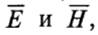 
а также векторами индукции 
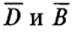электрического и магнитного полей. В проводящей среде, т. е. обладающей конкретной электропроводностью, распространение световых волн (видимого и ближнего ИК-диапазона), а также поведение их на границе раздела сред (веществ) описывается известной системой уравнений Максвелла.
Участие среды, в которой происходит распространение световых волн, описывается также известными материальными уравнениями, в которые входят ε 0, µ0 — диэлектрическая и магнитная постоянные вакуума; σ — удельная электропроводность вещества; µ и ε — относительная магнитная и диэлектрическая проницаемости вещества. Величины σ, µ, ε представляют собой материальные константы вещества, которые для однородного изотропного вещества являются скалярными величинами.
Известно, что в среде, помещенной во внешнее электрическое поле с напряженностью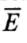 
под действием этого поля происходит перераспределение внутреннего электрического заряда (поляризация). В результате внешнее электрическое поле оказывается частично скомпенсированным внутренним полем, связанным с перераспределением зарядов. Если вектор 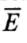описывает внешнее электрическое поле, то вектор 
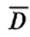суммарное поле, связанное как с наложением внешнего электрического поля, так и с перераспределением зарядов (поляризацией). Вектор 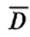представим в виде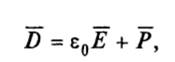 
Где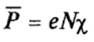 
вектор поляризации среды, определяемый суммарным дипольным моментом c единицы объема вещества. В некоторых не магнитных материалах, таких, например, как полупроводники, в оптическом диапазоне длин волн µ = 1. Кроме того, рассматриваемые материалы имеют значительную электропроводность (σ ≈ 0), и в материале (веществе) происходит растекание и рассасывание объемного заряда вплоть до значения ρ = 0.
|
|
|
Решая совместно уравнения Максвелла и материальные уравнения для среды, у которой µ = 1 и ρ = 0, получаем
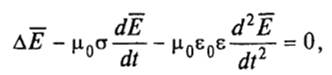(1)
где ∆ — оператор Лапласа (∆ = ∇ 2 — дивергенция градиента). Выражение (1) является волновым уравнением, связывающим световую волну и параметры вещества.
4. 1 Оптические постоянные материала и нахождение их по спектрам поглощения
В однородной изотропной среде решение волнового уравнения (1) может быть представлено в виде плоской волны. В системе координат, в которой волновой вектор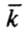 
этой волны направлен вдоль оси z (kх, ky = 0) так, что Еz = 0. Тогда компоненты Ех и Еy вектора напряженности электрического поля могут быть представлены в виде
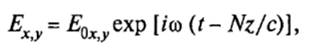(2)
Где
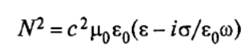(3)
— постоянная распространения света в веществе (среде). Путем прямой подстановки (2) в (1) можно легко убедится, что рассмотренная плоская волна является решением этого уравнения, если постоянная распространения N удовлетворяет (3). Так как с2 = 1/(µ0ε 0), то соотношение (3) может быть представлено в более простом виде
(4)
где ω — круговая частота световой волны. Таким образом, величина N является комплексной и в ней можно выделить вещественную и мнимую составляющие.
В частном случае, когда электропроводность среды на соответствующей частоте обращается в нуль (σ = 0), т. е. на этой частоте вещество ведет себя как диэлектрик (стекло), постоянная распространения N является вещественной и N2 = ε. Это совпадает с известным соотношением для диэлектриков, которое связывает относительную диэлектрическую проницаемость ε и показатель преломления света n в веществе в виде ε = n2. Поэтому в случае диэлектриков (σ = 0) N = n, т. е. совпадает с показателем преломления вещества и в соответствии с выражениями (2) описывает набег фазы электромагнитной волны в веществе.
|
|
|
В общем случае, когда σ ≠ 0, постоянная распространения должна быть записана на основании (4) в виде
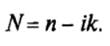(5)
Эта величина называется комплексным показателем преломления. Чтобы раскрыть физический смысл вещественной и мнимой составляющих постоянной распространения N, подставим (5) в (2), тогда
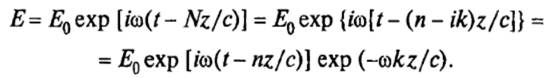
Экспонента вида exp(− ω kz/c) является вещественной убывающей функцией, которая в произведении с амплитудой E0 заставляет ее убывать с ростом координаты z, т. е. описывает затухание этой электромагнитной волны.
Таким образом, для σ ≠ 0 и, соответственно, k ≠ 0 амплитуда световой волны экспоненциально затухает. В однородной среде это затухание является следствием поглощения. Поэтому мнимая составляющая постоянной распространения (величина k) называется показателем поглощения (показателем экстинкции — светоослабления).
Второй экспоненциальный множитель exp (iω [t − nz/c]) имеет чисто мнимый аргумент. Поэтому этот множитель описывает набег фазы электромагнитной волны, а n, как и ранее, называется показателем преломления вещества.
Комплексный показатель преломления N, а также его вещественная n и мнимая k составляющие представляют собой оптические постоянные вещества (среды). Наряду с N, n и k могут быть использованы и другие оптические постоянные. В частности, в оптических измерениях производится измерение не амплитуды Е (или Н), а интенсивности I световых волн, которая пропорциональна квадрату амплитуды I~Е2. Таким образом,
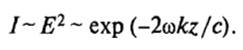(6)
С другой стороны, экспоненциальный характер затухания светового потока дается законом Бугера в виде
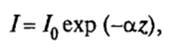(7)
где α — коэффициент поглощения, который также представляет собой оптическую постоянную вещества. Коэффициент поглощения α описывает затухание потока излучения на единицу длины пути и имеет размерность, обратную длине, в то время как k является безразмерной величиной.
Сравнивая величины (7) и (6), находим соотношение
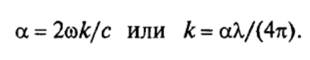(8)
Соотношение (8) связывает коэффициент поглощения α и показатель поглощения k вещества. Обе эти величины являются равноправными. Коэффициент поглощения α более широко используется при описании экспериментальных данных в оптико-физическом эксперименте в области не очень сильного поглощения. В то же время показатель поглощения k более широко используется в теории, а также для описания данных эксперимента в области сильного поглощения.
|
|
|
По аналогии с диэлектриками (стеклами) можно обобщить соотношение (5) на проводящие среды (например, полупроводниковый материал или керамику):
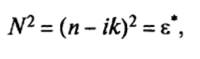(9)
где ε * — комплексная диэлектрическая проницаемость:
(10)
откуда найдем вещественную и мнимую составляющие диэлектрической комплексной проницаемости ε 1 = n2 − k2 и ε 2 = 2nk. Соотношения (9) и (10) переходят в соотношения ε = n2 при σ = 0 или k = 0. Таким образом, эти условия равноправны. Следовательно, на линиях поглощения параметры k и σ являются конечными величинами. За пределами полос поглощения они опять принимают нулевые значения. Вещественная ε 1 и мнимая ε 2 составляющие комплексной диэлектрической проницаемости также являются материальными константами вещества. Использование оптических постоянных n, k или ε 1 и ε 2 по своей сути является равноправным за исключением теоретической кристаллооптики, где ε является тензорной величиной.
В оптическом диапазоне частот более употребляемыми являются величины n и k, так как здесь эти величины могут быть довольно легко найдены раздельно прямым методом измерений. В то же время независимое экспериментальное определение величин ε 1 и ε 2 на оптических частотах представляет определенную трудность.
В диапазоне же радиочастот довольно легко измерить вещественную и мнимую составляющие диэлектрической проницаемости, тогда как измерение показателей преломления и поглощения в этом диапазоне более сложно.
|
|
|
