 |
4.2 Определение оптических постоянных по спектрам отражения
|
|
|
|
Метод Крамерса-Кронига используется в основном для численного анализа спектров отражения твердых тел. Если показатель преломления N является комплексной величиной, то коэффициент отражения на границе вещество-воздух (N = 1) является также комплексной величиной:
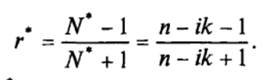
Это значит, что r * описывает изменение вектора, а именно изменение его амплитуды и фазы.
Амплитудный коэффициент отражения r * формально может быть записан в виде
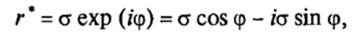 (11)
(11)
где σ — изменение амплитуды вектора при отражении; ϕ — набег фазы отраженной волны.
Так как интенсивность световой волны пропорциональна квадрату напряженности электрического поля I~Е 2, то коэффициент отражения для интенсивности световых волн (наблюдаемый в экспериментах) является вещественной величиной и дается известным выражением
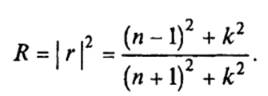 (12)
(12)
Очевидно, что величины σ и R в (11) и (12) связаны соотношением
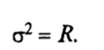
В частном случае, когда поглощение отсутствует (k = 0), амплитудный коэффициент отражения является вещественной величиной,
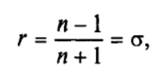
а набег фазы составляет ϕ = π.
Между вещественной и мнимой составляющими коэффициента отражения r существует взаимно однозначная связь, определяемая интегральным соотношением, связывающим амплитуду и фазу амплитудного отражения:
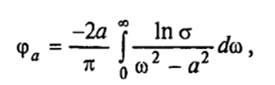 (13)
(13)
где коэффициент отражения lnr * = ln σ − iϕ.
Соотношение (13) позволяет сделать важный вывод, что по результатам измерений коэффициента отражения R, выполненных в широком диапазоне длин волн, может быть определен фазовый угол ϕ а для любой частоты ω = а. На практике интегрирование выражения (13) достаточно выполнить в области спектра, где отчетливо видна зависимость коэффициента отражения от частоты излучения, т. е. в области полос поглощения и вблизи них. За пределами этих полос, где коэффициент отражения остается практически постоянным, в числителе выражения (13) под знаком интеграла стоит константа. Здесь фазовый угол ϕ а = 0.
|
|
|
Приравняв вещественные и мнимые составляющие в выражениях для r *, можно показать, что
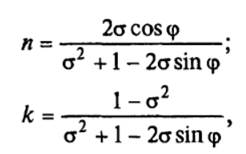 (14)
(14)
где σ и ϕ находятся из выражений (11)–(13) по измеренному коэффициенту отражения R.
Таким образом, процедура определения n и k методом Крамерса-Кронига из спектров отражения включает этапы:
1) измерение спектра отражения в области, где наблюдается выраженная зависимость коэффициента отражения от частоты излучения;
2) определение по (13) фазового набега ϕ при отражении;
3) вычисление по формулам (14) на основании найденных σ 2 = R и ϕ искомых оптических констант n и k.
Данная методика Крамерса-Кронига применима для твердых тел, в том числе для полупроводниковых материалов.
5. ИЗМЕРЕНИЕ ОПТИЧЕСКИХ ПАРАМЕТРОВ ЖИДКИХ СРЕД
Распространение излучения в жидкой среде связано с процессом поглощения и рассеяния, и поэтому к ранее рассмотренным для твердых тел параметрам N, n, k, α (ε 1, ε 2, ε *) необходимо для жидких сред прибавить параметры, характеризующие рассеяние. К ним относятся σ (γ ) — коэффициент рассеяния в направлении под углом γ относительно направления распространения излучения, σ — коэффициент рассеяния в телесном угле, равном 4π. Относительное распределение рассеянного излучения по углам описывается функцией
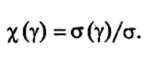
Эта характеристика называется индикатрисой рассеяния. Если χ (γ ) = 1, то индикатриса рассеяния является сферической.
Если пренебречь поляризационными свойствами излучения, то знание коэффициентов поглощения α и рассеяния σ и индикатрисы рассеяния χ (γ ) вполне достаточно, чтобы описать процессы распространения излучения в жидкой среде. Однако при решении ряда задач рассматриваются другие величины: ε = α + σ — коэффициент ослабления; Λ = σ /(α + σ ) — вероятность выживания фотона (альбедо однократного рассеяния); β = α /σ — удельное поглощение. Здесь все основные параметры относятся к монохроматическому излучению. В тех случаях, если необходимо решение задачи в широком спектральном диапазоне, где оптические свойства жидкой среды не остаются постоянными, нужно три указанных выше параметра α, σ, σ (γ ) измерять во всем спектральном диапазоне.
|
|
|
Изменение энергетической яркости излучения при прохождении элементарного участка длиной dl определяется выражением
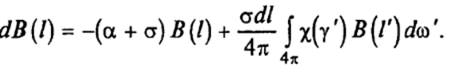 (15)
(15)
Первое слагаемое определяет поглощение излучения на участке dl, а второе слагаемое учитывает часть рассеянного света, поступающего на элемент dl от других элементов dl′, в элементарном угле dω ′. Уравнение (15) называется уравнением переноса излучения в жидкой рассеивающей среде и в соответствии с различными граничными условиями широко используется для решения различных задач.
Поглощение излучения связано с «работой» атомов и молекул. Интенсивность и спектры поглощения связаны с составом жидкой среды, числом атомов и молекул, числом электронов и характером взаимодействия между ними. Дискретные спектры поглощения присущи изолированным атомам и простым молекулам. Сплошные спектры поглощения присущи средам, состоящим из сложных молекул, к которым относится вода Мирового океана и содержащиеся в ней компоненты органического и неорганического происхождения. Поэтому спектр поглощения реальной водной среды является сплошным, имеет место поглощение фотонов любой длины волны, но с разной вероятностью поглощения. Причиной рассеяния света является оптическая неоднородность жидкой среды, которая характеризуется комплексным показателем преломления N. Непостоянство данного параметра в пространстве приводит к возникновению рассеянного излучения.
Природа оптической неоднородности разнообразна. В одних случаях она возникает из-за инородных тел, имеющихся в среде (частицы, пузырьки воздуха). В других случаях среда может не содержать постоянных включений, однако вследствие флуктуаций плотности вещества и ориентации молекул в ней создаются «сгустки» и «разрежения» показателя преломления. Возникающее на таких неоднородностях рассеяние называется молекулярным.
|
|
|
Поскольку колебания молекул существуют при любых температурах, то молекулярное рассеяние имеет место и в абсолютно чистой воде. Наличие в воде растворенных веществ порождает флуктуации их концентрации в разных участках пространства, что также вызывает дополнительное молекулярное рассеяние. Наконец, в реальной жидкой среде вследствие разных причин наблюдается перемещение масс различной температуры и плотности (турбулентность). Это приводит к крупным оптическим неоднородностям, на которых рассеивается излучение.
В реальной жидкой среде (вода Мирового океана) также содержится большое количество частиц как минералогического, так и органического происхождения. Минеральные частицы в видимой части спектра имеют показатель преломления n = 1, 13–1, 17, иногда n = 1, 25. У органических же частиц n1, 05. Показатель преломления воздушных пузырей n = 1, 75. Размеры частиц колеблются от 0, 01 до 1000 мкм.
Теорию рассеяния света на частицах размером d < < λ создал Релей. В основе этой теории лежит электронная теория Максвелла с определенными граничными условиями для сферической поверхности частиц. Если релеевская частица (d < < λ ) не поглощает свет (α = 0), то коэффициент рассеяния, обусловленный только посторонними вкраплениями, равен
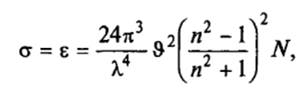 (16)
(16)
где N — число частиц в единице объема ϑ.
Из формулы (16) видно, что величина рассеянного потока пропорциональна λ − 4. Индикатриса рассеяния на релеевских частицах описывается формулой

С ростом размера частицы (d ≈ λ ) индикатриса рассеяния из симметричной превращается в асимметричную. Доля света, рассеянного в переднюю полусферу, увеличивается (рассеяние вперед). Асимметрия характеризуется коэффициентом асимметрии, равным отношению световых потоков, рассеянных в переднюю и заднюю полусферы.
В реальной практике в большом объеме производятся измерения индикатрисы рассеяния жидких сред, позволяющие определить состав среды. Разработан ряд методов и средств для исследований жидких сред в локальных лабораториях или в масштабах Мирового океана. Метод измерения χ (γ ) основан на фотометрировании жидкой среды фотоприемным устройством с большим угловым разрешением под разными углами наблюдения элементарного объема жидкой среды, освещенного узким пучком света. При этом измеряется поглощение, рассеяние и индикатриса рассеяния. Приборы данного типа получили название фотометр-нефелометр. К тому же на них проводятся и спектральные измерения.
|
|
|
|
|
|


