 |
Расчет зубчатой ременной передачи
|
|
|
|
Перспективным видом гибкой связи является зубчатые ремни. Они имеют высокую тяговую способность и сравнительно большой КПД. Передачи этого типа работают без смазки, устойчивы к действию абразивных и агрессивных сред, позволяет синхронизировать движения входного и выходного звеньев, просты в эксплуатации.
В отличие от плоских, клиновых и поликлиновых передач в зубчатых ременных передачах движение передается посредством сил трения, а также зацеплением ремня и шкивов, т.е. устанавливается достаточно жесткая кинематическая связь между ведущими и ведомыми звеньями механизмов.

Простейшая передача с зубчатым ремнем состоит из ведущего 1, ведомого 2 шкивов и охватывающего их зубчатого ремня 3.
Вычисляем общее передаточного отношения механизма робота по формуле:
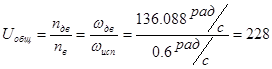
Так как в механизме две ступени, то мы принимаем UЗР=2, а UВП=114.
Определяем момент, мощность и частоту вращения на ведомом шкиве зубчато-ременной передачи: момент: Т2=Т1Ä UЗРÄhlуч=1.7Ä2Ä0.99Ä0.96=3.231 НÄм, частота вращения:

Мощность Р2=Р1Ählуч=360Ä0.99Ä0.96=342,144 Вт. По величине крутящего момента на ведущем шкиве из справочника выбираем модуль зубчатого ремня m=3 мм.
Определим число зубьев малого шкива из справочника по модулю зубчатого ремня. Если m=3, то Z1=14.
Зная передаточное отношения зубчатого ремня, определим число зубьев ведомого шкива. Z2 = Z1Ä. UЗР =14Ä2=28.
Диаметры ведомого и ведущего шкива:
d1 = mÄZ1 =3Ä14=42 мм.
d2 = mÄZ2 =3Ä28=84 мм.
Вычисляем окружную скорость ремня Vокр используя зависимость:

Действительная частота вращения ведомого шкива:

Уточненное передаточное отношение:
|
|
|

Межосевое расстояние вычисляем как а=1,5 (d1+d2) =1,5 (42+84) =252 мм. Определяем длину ремня из формулы:

Число зубьев ремня (расчетное)

Количество зубьев ремня округляем до стандартного  . Когда выбрали число зубьев, уточним длину ремня:
. Когда выбрали число зубьев, уточним длину ремня:
 мм
мм
Сила, передаваемая зубчатым ремнем:
 Н
Н
Коэффициент КF принят равным единице для спокойной пусковой нагрузки.
Расчетную допускаемую удельную силу на ремне определяем по зависимости: FY= [F] 0ÄCUÄCzÄCp
Где 
CU =1
Cz=1
Cp=0.9
FY=9Ä1Ä1Ä0.9=8,1 H/мм.
Число зубьев ремня, находящихся в зацеплении с ведущим и ведомым шкивами, вычислим:





Принимаем Z1з=7

Принимаем Z2з=15
Определим необходимую ширину ремня:
 мм
мм
Где q=4Ä10-4 кг/ (мÄмм) - погонная масса
Сш=1.05 - Коэффициент, учитывающий неполноту витков каната у боковых поверхностей ремня.
Принимаем ширину ремня в соответствии со стандартным рядом В=32мм.
Рассчитаем удельное давление на рабочих поверхностях зубьев ремня и сравним с допускаемым:

где  - коэффициент концентрации нагрузки на зубьях, по их высоте и длине; h - высота зуба; [P] =0,75МПа - допускаемое давление на зубья ремня, зависящее от частоты вращения ведущего вала.
- коэффициент концентрации нагрузки на зубьях, по их высоте и длине; h - высота зуба; [P] =0,75МПа - допускаемое давление на зубья ремня, зависящее от частоты вращения ведущего вала.
Условие удельного давления Р< [Р] 0,63МПа<0,75МПа выполняется.
Величину начального натяжения ремня F0 вычислили по эмпирической зависимости:
 Н
Н
Силу, действующую на вал передачи, определяем:
Fr=1.1Ä FT=1.1Ä80,95=89,045 H.
Для динамического анализа зубчатой ременной передачи рассчитываем критическую линейную скорость ремня в такой последовательности:
а) Из справочника для ремня с модулем m=3 находим собственную частоту  с-1
с-1
б) Определим натяжение ведущей и ведомой ветвей ремня:
Fвщ = F0+0.5ÄFT = 43,173+0.5Ä80,95 =83,65 Н
Fвд = F0-0.5ÄFT = 43,173-0.5Ä80,95 = 2,7 Н
в) Определим деформацию одного шага ведущей и ведомой ветви ремня:
|
|
|

a' =14Ä10-4 мм2/Н - выбирается из справочника.
xс1 = aÄFвщ =4,375Ä10-5Ä83,65 = 0.00366 мм;
xс2 = aÄFвд =4,375Ä10-5Ä2,7 =0.000517 мм.
г) находим критическую скорость зубчатого ремня:
при КВ=0.5Ä (ZP-Z1З-Z2з) =0.5 (75-7-15) =26;
получаем для ведущей ветви ремня:

для ведомой ветви ремня:

Следовательно, передача работает в дорезонансной зоне, т.к. Vокр<Vкр и не требует корректировку параметров.
Основные параметры зубчатого ремня и шкивов.
| Параметры | Обозначения | Расчетные формулы и результаты расчета |
| 1 | 2 | 3 |
| Модуль зацепления, мм | m | 3 |
| Число зубьев ремня | ZP | 75 |
| Шаг ремня, мм | РР | 9,42 |
| Ширина зуба ремня, мм | S | 3 |
| Высота зуба ремня, мм | h | 2 |
| Толщина каркаса ремня, мм | H | 4 |
| Расстояние от впадины зуба до нейтрального слоя ремня, мм | d | 0.6 |
| Угол профиля зуба, град | g | 40 |
| Ширина ленты, мм | В | 32 |
| Ширина зуба шкива, мм | Sш | 3,2 |
| Высота зуба шкива, мм | hш | 3,0 |
| Межосевое расстояния, мм | а | 252 |
| Делительный диаметр ведущего шкива, мм | d1 | 42 |
| Делительный диаметр ведомого шкива, мм | d2 | 84 |
| Диаметр вершина зубьев ведущего шкива, мм | da1 | 40.81 |
| Диаметр вершина зубьев ведомого шкива, мм | da2 | 82,82 |
| Диаметр впадины зубьев ведущего шкива, мм | df1 | 35.41 |
| Диаметр впадины зубьев ведомого шкива, мм | df2 | 77,42 |
| Радиус закругления головки зубьев, мм | r3 | 1.05 |
| Радиус закругления впадины зубьев, мм | r4 | 1.2 |
| Длина зуба, мм | В3 | 35 |
Расчет волновой передачи
При конструировании модуля поворота руки робота необходимо выдержать ряд требований:
1. Большое передаточное отношение при сравнительно небольшом количестве деталей.
2. Высокая нагрузочная способность зацепления.
3. Сравнительно высокий КПД ( =0,92).
=0,92).
4. Высокая кинематическая точность и плавность хода.
Эти требования привели к необходимости использования волновой передачи как основного механизма обеспечения требуемых показателей.
Исходные данные:
 - крутящий момент на тихоходном валу;
- крутящий момент на тихоходном валу;
 - число оборотов вала генератора;
- число оборотов вала генератора;
 -передаточное отношение редуктора;
-передаточное отношение редуктора;
 -время работы редуктора;
-время работы редуктора;
возможная перегрузка по Мт в 2.5 раза.
Расчет волновой зубчатой передачи выполняется в 2 этапа: первый - проектировочный, второй - проверочный.
Проектировочный расчет заключается в предварительном определении размеров гибкого колеса: диаметра, длины, ширины, толщины стенок, ширины зубчатого венца.
|
|
|
При проектировочном расчете удобно исходить из критерия износостойкости боковых поверхностей зубьев в связи с тем, что удельное давление на зубья зависит от основных конструктивных параметров гибкого колеса.
Проверочный расчет сводится к проверке удовлетворения волновой передачи критериям работоспособности.
На первом месте по значению стоит критерий прочности. По этому критерию должны проверяться все волновые передачи. Остальные критерии должны учитываться в зависимости от условий работы ВЗП.
Проектировочный расчет
Кинематическая схема передачи соответствует схеме, показанной на рис.1
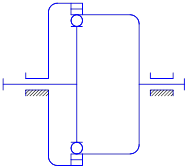
Рис.1
Принимаем  ;
;  . Число зубьев гибкого колеса
. Число зубьев гибкого колеса  . Число зубьев жесткого колеса
. Число зубьев жесткого колеса  . Назначаем тип генератора - кулачковый с одним рядом шариков. Для гибкого колеса выбираем сталь 20Х2Н4А с HRC 28…32, для жесткого - сталь 40Х с HRC 28…32. Назначаем конструктивные относительные параметры гибкого колеса:
. Назначаем тип генератора - кулачковый с одним рядом шариков. Для гибкого колеса выбираем сталь 20Х2Н4А с HRC 28…32, для жесткого - сталь 40Х с HRC 28…32. Назначаем конструктивные относительные параметры гибкого колеса:  - относительная толщина стенки под зубчатым венцом;
- относительная толщина стенки под зубчатым венцом;  - относительная толщина гладкой оболочки;
- относительная толщина гладкой оболочки;  - относительная ширина зубчатого венца;
- относительная ширина зубчатого венца;  -относительная длина гибкого колеса.
-относительная длина гибкого колеса. 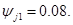 Определяем допускаемое удельное давление на поверхности зубьев:
Определяем допускаемое удельное давление на поверхности зубьев:

где  - коэффициент, учитывающий влияние передаточного отношения;
- коэффициент, учитывающий влияние передаточного отношения;
 при i>=100 т.к. в данном случае.
при i>=100 т.к. в данном случае.
 - коэффициент, учитывающий тип генератора волн, для кулачкового генератора он равен единице;
- коэффициент, учитывающий тип генератора волн, для кулачкового генератора он равен единице;
 - допускаемое базовое удельное давление.
- допускаемое базовое удельное давление.
Определяем диаметр делительной окружности гибкого колеса:
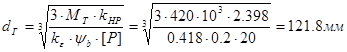
где  - коэффициент, учитывающий неравномерность распределения нагрузки по зубьям;
- коэффициент, учитывающий неравномерность распределения нагрузки по зубьям;  - коэффициент многопарности зацепления.
- коэффициент многопарности зацепления.
Определяем приближенное значение модуля зацепления:
 ;
;
принимаем ближайшее стандартное значение  .
.
Определяем диаметры делительных окружностей гибкого и жесткого колес:

 .
.
Принимаем в соответствии с рекомендациями  .
.
Определяем коэффициент смещения гибкого и жесткого колес:
|
|
|
 ;
;
 .
.
Определяем максимально возможную высоту захода зубьев:

Определяем диаметры окружностей впадин и вершин гибкого колеса:
 ;
;
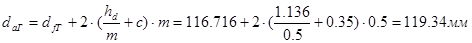 .
.
Окончательное значение диаметра окружности вершин принимается после проверок:
· Высота зуба не должна быть больше, чем у производящего исходного контура: 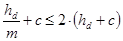 подставляем 2,622<3,272 - выполняется;
подставляем 2,622<3,272 - выполняется;
· Высота зуба не должна быть больше толщины оболочки гибкого колеса под зубчатым венцом 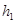 :
:  подставляем значения и получим 1,311<1,368 - выполняется.
подставляем значения и получим 1,311<1,368 - выполняется.
Определяем диаметры окружностей вершин и впадин жесткого колеса:
 мм.
мм.
 ,
,
где  - диаметр окружности выступов.
- диаметр окружности выступов.
Определяем наличие радиального зазора между вершинами зуба гибкого колеса и впадиной жесткого колеса по большой оси генератора:

подставляем значения и получаем 16,621>0.075 - условие выполняется.
Определяем основные окружности гибкого и жесткого колес:
 ;
;
 .
.
Определяем толщины зубьев гибкого и жесткого колес по делительным окружностям:
 мм.
мм.
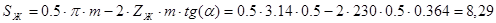 . мм.
. мм.
Определяем размеры по роликам:
 ,
,
 ,
,
где D - диаметр мерительного ролика, берется в пределах (1,7.2) *m из набора для измерения резьбы: 0.572, 0.796, 1.008, 1.157, 1.302 и т.д. или по ГОСТ 2475-62;  - угол давления в точке касания ролика с профилем зуба, находиться по таблице инволют.
- угол давления в точке касания ролика с профилем зуба, находиться по таблице инволют.
Определяем конструктивные размеры гибкого и жесткого колес:
a) Гибкое колесо:
 - толщина стенки;
- толщина стенки;
 - толщина гибкой оболочки;
- толщина гибкой оболочки;
 - ширина зубчатого венца гибкого колеса;
- ширина зубчатого венца гибкого колеса;
 - длина гибкого колеса;
- длина гибкого колеса;
b) Жесткое колесо:
 - ширина зубчатого венца жесткого колеса;
- ширина зубчатого венца жесткого колеса;
 - толщина обода жесткого колеса;
- толщина обода жесткого колеса;
 -средний радиус жесткого колеса.
-средний радиус жесткого колеса.
Проверочный расчет
Проверка по критерию прочности
Определяем амплитудные нормальные (изгибные) напряжения в гибком колесе ненагруженной ВЗП:
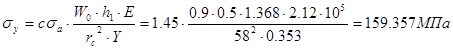 ,
,
где  - коэффициент, величина которого зависит от формы деформирования;
- коэффициент, величина которого зависит от формы деформирования;
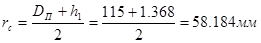 ;
;
 - коэффициент влияния зубьев; Е - модуль упругости.
- коэффициент влияния зубьев; Е - модуль упругости.
Определим амплитудные нормальные напряжения в гибком колесе при действии крутящего момента:
 ,
,
где  - коэффициент, учитывающий влияние конструкции генератора волн на интенсивность увеличения напряжений в гибком колесе.
- коэффициент, учитывающий влияние конструкции генератора волн на интенсивность увеличения напряжений в гибком колесе.
Определяем средние напряжения:
 .
.
Определяем максимальные касательные напряжения в гибком колесе ненагруженной волновой передачи:
 .
.
Определяем максимальные касательные напряжения в гибком колесе нагруженной волновой передачи:

 ,
,
где  - коэффициент, учитывающий влияние крутящего момента и конструктивных параметров гибкого колеса на уровень касательных напряжений в нем.
- коэффициент, учитывающий влияние крутящего момента и конструктивных параметров гибкого колеса на уровень касательных напряжений в нем.
|
|
|
Определяем амплитудные и средние касательные напряжения:
 ;
;
 .
.
Определяем эффективные коэффициенты концентрации напряжений:
 ;
;
 ,
,
где  - коэффициент, учитывающий влияние радиуса сопряжения контура зуба с линией его впадины.
- коэффициент, учитывающий влияние радиуса сопряжения контура зуба с линией его впадины.
Определяем запас прочности гибкого колеса:
 ;
;
 ;
;
 .
.
Условие n>1.3 выполняется.
Проверка по критерию "ресурс подшипника генератора волн".
Определяем основные геометрические и конструктивные параметры кулачкового генератора волн:
·  - наружный диаметр круглого подшипника с гибкими кольцами;
- наружный диаметр круглого подшипника с гибкими кольцами;
·  - толщина наружного кольца;
- толщина наружного кольца;
·  - толщина внутреннего кольца;
- толщина внутреннего кольца;
·  - диаметр шариков;
- диаметр шариков;
·  - ширина колец генератора;
- ширина колец генератора;
·  - глубина дорожки качения наружного кольца;
- глубина дорожки качения наружного кольца;
·  - глубина дорожки качения внутреннего кольца;
- глубина дорожки качения внутреннего кольца;
·  - число шариков;
- число шариков;
·  - радиус желоба дорожки качения.
- радиус желоба дорожки качения.
Определяем максимальную деформацию по генератору:
 .
.
Определяем располагаемую динамическую грузоподъемность шарикоподшипника генератора:
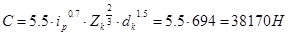 .
.
Определяем потребную динамическую грузоподъемность:

Проверка по критерию жесткость звеньев.
Определяем предельный крутящий момент, передаваемый волновым зубчатым редуктором:
 ,
,
где 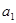 - коэффициент податливости гибкого колеса; G - модуль упругости при сдвиге;
- коэффициент податливости гибкого колеса; G - модуль упругости при сдвиге;  - коэффициент податливости жесткого колеса;
- коэффициент податливости жесткого колеса;  - податливость генератора.
- податливость генератора.
Принимаем радиальное биение вала  .
.
Определяем максимальный крутящий момент:
 ,
,
где  - коэффициент перегрузки.
- коэффициент перегрузки.
Проверка по критерию "теплостойкость".
Определяем количество тепла, образующегося в результате потерь мощности:
 .
.
Определяем количество тепла, отводимого в окружающую среду от передачи:
 ,
,
где  - коэффициент передачи с площади F1; F1 определяется после эскизного проектирования.
- коэффициент передачи с площади F1; F1 определяется после эскизного проектирования.
Так как А1>А, то условие выполняется.
Конструирование механизма
Механизм в данном проект можно оставлять стандартным (протоколом М4), но учитывая особенности расчётов. Конструкция механизма поворота руки робота показана на формате А1 в приложении к курсовой работе.
Конструкция выполняется по расчетам, но выбирается по конструктивным соображениям и стандартами с явным запасом прочности. Это облегчает задачу проектирования механизма, но этот проект даёт только навыки к проектированию. На самом деле при более серьезной проектировке надо рассчитывать каждый элемент механизма и, по возможности, выбирать таковой согласно стандартом.
Расчёт на прочность валов
Расчёту подлежат те валы, которые в данном механизме воспринимают нагрузки. Определим потребный диаметр вала на ведущем шкиве учитывая прочностные характеристики. Это является проектировочным расчётом.

где Т - крутящий момент на валу, [tкр] - допускаемое напряжения при кручении.

Так как расчётная величина является очень малой конструктивно для удобства и возможности шпоночного соединения выбираем вал с d = 18 мм., при этом выигрывая большой запас прочности и такой же диаметр имеет вал электрического двигателя, а это упрощает задачу конструирования. Определим потребный диаметр вала на ведомом шкиве учитывая прочностные характеристики. Это является проектировочным расчетом.

Принимаем диаметр вала d=15 мм, это нам даст большой запас прочности и облегчит задачу проектирования.

Принимаем диаметр вала d=45 мм, это нам даст большой запас прочности и облегчит задачу проектирования.
Проверочный расчет

Материал вала - сталь 45, нормализация, σв=590Нмм2.
предел выносливости при симметричном цикле изгиба:
 Н/мм2
Н/мм2
предел выносливости при симметричном цикле касательных напряжений:
 Н/мм2.
Н/мм2.
Сечение А-А.
Концентрацию напряжений вызывает наличие шпоночной канавки.
Принимаем κτ=1.58, кσ=1б49, масштабный фактор εσ=ετ=0.82, ψτ=0.1;
Крутящий момент М=210·103Нм.
Изгибающий момент в горизонтальной плоскости:
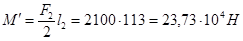

Изгибающий момент в вертикальной плоскости:
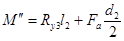
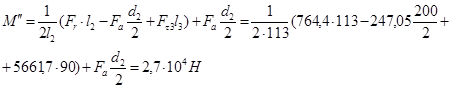
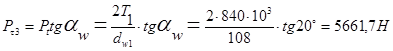
Суммарный изгибающий момент в сечении А-А.
 Нмм
Нмм
Момент сопротивления изгибу:

Момент сопротивления кручению:

Амплитуда нормальных напряжений изгиба:
 среднее значение σm=0;
среднее значение σm=0;
Коэффициент запаса прочности по нормальным напряжениям:
 ;
;
Коэффициент запаса прочности по касательным напряжениям

Результирующий коэффициент запаса прочности для сечения А-А

Расчёт подшипников
По динамической грузоподъемности подбирают подшипники качения при п=> 10 мин. - Ä1 Подшипник подбирается по условию: Сп<=Ср, где Сп - потребная динамическая грузоподъемность, Ср - располагаемая динамическая грузоподъемность.
Динамическую грузоподъемность определяют по формуле:
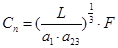
где а1 = 0.44, а23=1 - коэффициенты, учитывающие качество материалов подшипника, смазку и условия эксплуатации:

промышленный робот модуль

Эквивалентную нагрузку F для различных типов подшипников определяют по формуле:
в частности для радиальных.
F=VÄFaÄKdÄKT
V = 1 (вращается внутреннее кольцо); KdÄ = 1 (спокойная нагрузка);
KT = 1 (температурный коэффициент).
Fr = 31.62Н
FВ = (FrÄ50) /700= 2.26Н
FА= Fr+FВ => FА = 34Н
F = 1Ä34Ä1Ä1 = 34Н

Находим
Выбираем стандартный подшипник
№1000905
Внутренний диаметр d = 20мм;
Внешний диаметр D = 37мм;
Ширина В = 9мм;
Радиус округления r = 0,5мм;
Грузоподъемность С = 574Н;
Статическая грузоподъемность С = 375Н;
Шарики DT = 5мм;
Число шариков Z = 12шт;
Масса 0.042кг.
|
|
|


