 |
Источники гетероскедастичности
|
|
|
|
Понятие гетероскедастичности остатков
При проведении регрессионного анализа, основанного на методе наименьших квадратов, на практике следует обратить серьезное внимание на проблемы, связанные с выполнимостью свойств случайных отклонений моделей.
Классический регрессионный анализ предполагает, что дисперсия ошибок измерения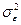 
постоянна, то есть все наблюдения зависимой переменной имеют одну и ту же постоянную дисперсию ошибки наблюдения, (такая модель называется гомоскедастичной).
Если же дисперсия ошибок измерения для разных значений зависимой переменной непостоянна, такую модель называют гетероскедастичной.
Гетероскедастичность остатков – это свойство остатков, которое заключается в том, что их дисперсии или разбросы для каждого фиксированного Х являются неоднородными или неодинаковыми.
Т.е. не выполняется предпосылка 2 использования МНК:
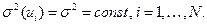
Если истинная зависимость описывается уравнением
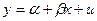
и изменения значений невключенных переменных, и ошибки измерения, влияя на случайный член, делают его сравнительно малым при малых у и х и сравнительно большим — при больших у и х, то экономические переменные часто совместно меняют свой масштаб.
На практике гетероскедастичность не так уж и редка. Рассмотрим два примера линейной регрессии ‒ зависимости потребления С от дохода I: 
.
Рис. 1. Примеры зависимости потребления С от дохода I
В обоих случаях с ростом дохода растет среднее значение потребления. Но если на рис.1.а. дисперсия потребления остается одной и той же для различных уровней дохода, то на рис.1.б. при аналогичной зависимости среднего потребления от дохода дисперсия потребления не остается постоянной, а увеличивается с ростом дохода.
|
|
|
Фактически это означает, что во втором случае субъекты с большим доходом в среднем потребляют больше, чем субъекты с меньшим доходом, и, кроме того, разброс в их потреблении более существенен для большего уровня дохода. Фактически люди с большими доходами имеют больший простор для распределения своего дохода. Разброс значений потребления вызывает разброс точек наблюдения относительно линии регрессии, что и определяет дисперсию случайных отклонений.
Динамика изменения дисперсий (распределений) отклонений для примера проиллюстрирована на рис. 2. При гомоскедастичности дисперсии ошибок постоянны, а при гетероскедастичности дисперсии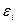 
изменяются (в примере ‒ увеличиваются).
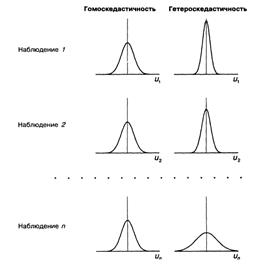
Рис. 2. Различия между гетероскедастичностью и гомоскедастичностью
Примеры моделей с гетероскедастичным случайным членом представлены на рис.3.
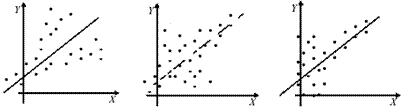
а) б) в)
Рис. 3. Примеры моделей с гетероскедастичным случайным членом
а) Дисперсия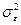 
растет по мере увеличения значений объясняющей переменной X.
б) Дисперсия 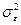имеет наибольшие значения при средних значениях X, уменьшаясь по мере приближения к крайним значениям.
в) Дисперсия ошибки наибольшая при малых значениях X, быстро уменьшается и становится однородной по мере увеличения X.
Источники гетероскедастичности
Гетероскедастичность характерна для перекрестных данных, когда учитываются экономические субъекты (потребители, домохозяйства, фирмы, отрасли и т.д.), имеющие различные доходы, размеры, потребности и т.д. В данном случае возможны проблемы, связанные с эффектом масштаба.
Гетероскедастичность возникает также и во временных рядах, когда зависимая переменная имеет большой интервал качественно неоднородных значений или высокий темп изменения (инфляция, технологические сдвиги, изменения в законодательстве, потребительские предпочтения и т.д.).
|
|
|
|
|
|
