Вычисление значений истинности формул логики высказываний

 

Покажем на примерах как вычисляется значение истинности формул логики высказываний при заданных значениях истинности входящих в формулу пропозициональных переменных и констант. Для этого воспользуемся универсальным для логики высказываний методом – методом истинностных таблиц.

Прежде всего, заметим, что порядок вычисления значения истинности этой формулы определяется частично скобками, а частично старшинством операций. Этот порядок и вычисления в соответствии с ним представлены в таблице:

Результирующее значение И представлено в последней строке в столбце, соответствующем последней выполняемой операции отрицания Ø (в выделенной жирной линией клетке).

Предпоследнюю и последнюю строки в будущем будем объединять в одну, чтобы сократить размеры таблицы.

 

Тождественно-истинные и тождественно-ложные формулы логики высказываний. Логическая равносильность формул. Равносильные преобразования формул

 

Формулу логики высказываний, принимающую значение истинности И (истина) на любом наборе значений для пропозициональных переменных, входящих в формулу, называют тождественно-истинной формулой, или тавтологией.

Формулу логики высказываний, принимающую значение истинности Л (ложь) на любом наборе значений для пропозициональных переменных, входящих в формулу, называют тождественно-ложной формулой, или противоречием.

Формулу логики высказываний, не являющуюся ни тождественно-истинной, ни тождественно ложной, называют выполнимой.

Пусть формулы F и Ф логики высказываний содержит пропозициональные переменные X1, X2, …, Xn. Будем считать эти формулы логически равносильными, если они принимают одинаковые значения истинности на соответствующих наборах значений для пропозициональных переменных X1,X2,…,Xn, входящих в эти формулы.

Если множества пропозициональных переменных, входящих в формулы F и Ф не совпадают, то можно добиться этого совпадения, введя в ту или другую формулу недостающую переменную в качестве "фиктивной". Пусть, например, формула F не содержит пропозициональной переменной Xi. Тогда эту переменную можно ввести в формулу F "фиктивно", заменив формулу F на формулу FÚ(Xi&Ø Xi) или на формулу F&(XiÚØ Xi), которые на основании закона противоречия, закона исключенного третьего и свойств логических констант Л и И, равносильны F. Аналогично можно "фиктивно" ввести в формулы F и Ф все другие недостающие переменные. Это соображение легко распространить на любое число формул.

Как мы условились выше, тот факт, что формулы F и Ф логически равносильны будем обозначать FºФ.

Отношение равносильности формул, очевидно, обладает свойством транзитивности: если FºФ и ФºY, то FºY.

Приведенные выше свойства операций и законы логики высказываний, как легко проверить с помощью таблиц истинности, выражают логическую равносильность (эквивалентность) тех или иных формул.

Кроме приведенных выше равносильностей в логике высказываний большое значение имеют и другие, среди которых отметим следующие:

Логические равносильности играет важную роль в логике высказываний. Они фактически являются правилами и законами логических рассуждений, законами правильного мышления.[3]) Ниже мы покажем их применение, например, к анализу структуры математических доказательств.

На основании перечисленных выше равносильностей, к которым относятся свойства логических операций, логические законы и т.д., осуществляются равносильные (тождественные) преобразования формул логики высказываний с целью упрощения выражений или приведения к определенному виду (подобно тому, как это делается в школьной алгебре на основании свойств арифметических операций, алгебраических законов и иных тождественных соотношений).

 

Вывод следствий в логике высказываний

 

Пусть дана совокупность формул логики высказываний F={F1,F2,F3,…,Fm}. Формулы множества F называют посылками (или гипотезами). Определим понятие логического вывода формулы Ф из множества посылок (гипотез) F.

Вначале определим содержательно понятие логического следствия.

Будем говорить, что формула Ф является логическим следствием множества формул F1,F2,F3,…,Fn, если формула F1&F2&F3&…&FnÉФ является тождественно-истинной (или тавтологией).

Например, формула X является логическим следствием формул (ØXÉY) и (ØXÉØY), поскольку формула (ØXÉY)&(ØXÉØY)ÉX тождественно истинна, в чем легко убедиться с помощью таблицы истинности:

Ясно, что если две формулы равносильны, то каждая из них является логическим следствием другой.

Построение логического вывода некоторой формулы основывается на применении в процессе вывода специальных правил, называемых правилами вывода

Наиболее часто используются следующие правила вывода:

1. Правило замены формулы равносильной. В процессе вывода в любой момент любую формулу (или подформулу) можно заменить равносильной ей формулой.

Например, формулу Ø(AÚB) в любой момент можно заменить равносильной ей формулой ØA&ØB (второй закон Де Моргана), а формулу AÚØA - пропозициональной константой И (закон исключенного третьего).

2. Правило подстановки. Если в формулу F вместо всех вхождений пропозициональной переменной Xi подставить одну и ту же формулу F, то полученная в результате формула будет логическим следствием формулы F.

3. Правило modus ponens. Это правило позволяет из двух формул X и XÉY выводить третью формулу Y.

4. Правило modus tollens. Это правило формулируется так: из формул X&Y и ØY выводится формула ØX.

Формула ØX является логическим следствием формул X&Y и ØY в смысле приведенного выше определения, поскольку формула ((X&Y)&ØY)ÉØX является тождественно-истинной (тавтологией), в чем можно убедиться с помощью следующей таблицы истинности:

Например, из формул (AÚB)&C и ØC по правилу modus tollens выводится формула Ø(AÚB).

Итак, можно следующим образом более формально определить понятие логического вывода (и логического следования):

Логическим выводом (или просто, выводом) формулы Ф из множества посылок (гипотез) F={F1, F2, F3, …, Fm} называют последовательность формул вида: Ф1,Ф2,…,Фi-1,Фi,…,Фn=Ф, таких, что либо Фi - тавтология, либо ФiÎ F, либо Фi является конъюнкцией формул из F, либо Фi получена из формул множества F, или тавтологий логики высказываний, или ранее выведенных в данном выводе формул Ф1, Ф2, …,Фi-1 с помощью правил вывода.

Формулу Ф будем называть в этом случае логическим следствием множества формул F={F1,F2,F3,…, Fm}.

Тот факт, что формула Ф выводима из множества посылок F={F1,F2,F3,…, Fm} будем обозначать: F1,F2,F3,…, Fm |¾ Ф.

Заметим, что в соответствии с определением вывода все тавтологии логики высказываний считаются выводимыми формулами, притом из пустого множества посылок, то есть, если A - тавтология, то |¾A.

Примем без доказательства следующую теорему, которая называется теоремой дедукции.

Теорема дедукции:

Если F1,F2,F3,…, Fm |¾ Ф, то F1,F2,F3,…, Fm-1 |¾ (Fm ÉФ), и наоборот.

Эта теорема говорит о возможности переноса формул логики высказываний через знак выводимости |¾.

Замечание: m-кратное применение теоремы дедукции приведет к утверждению выводимости формулы

 

Применение логики высказываний к анализу математических

Доказательств

 

Ни у кого не возникает сомнения в том, что математические доказательства являются примерами строгих логических рассуждений.

Аппарат логики высказываний позволяет нам прояснить структуру доказательств многих математических утверждений.

Рассмотрим с точки зрения логики высказываний наиболее типичные методы доказательств в математике.

1. Доказательство с помощью построения цепочки импликаций.

Этим методом пользуются при доказательстве теорем, выраженных в форме импликации: "Если высказывание A истинно, то и высказывание B истинно", то есть AÉB.

Доказательство строится как последовательность тождественно-истинных импликаций вида: AÉA1, A1ÉA2, …, An-1ÉAn, AnÉB, где A1, A2, A3, …, An - некоторые вспомогательные высказывания.

Отсюда делается вывод (в силу транзитивности импликации) о справедливости теоремы AÉB.

Такое доказательство называется прямым доказательством.

Прежде, чем рассмотреть другие типы доказательств напомним классификацию теорем из средней школы, которую иллюстрирует рис.2.1

Как легко проверить, используя метод истинностных таблиц, прямая теорема оказывается равносильной обратной противоположной, а обратная теорема - противоположной. И в то же время, таких равносильностей в общем случае не существует между прямой и обратной теоремами, между прямой и противоположной, между обратной и обратной противоположной, между противоположной и обратной противоположной.

Из указанных равносильностей вытекает следующий метод доказательства.

2. Доказательство от противного.

Этот метод используется при доказательстве теорем вида AÉB и основывается на законе контрапозиции XÉY º ØY É ØX, который фактически гласит, что доказательство теоремы AÉB может быть заменено доказательством эквивалентной ей теоремы, которая формулируется как ØB ÉØA. Последняя теорема называется обратная противоположной (или противоположная обратной).

Доказательство теоремы ØB ÉØA осуществляется прямым путем, то есть как цепочка импликаций: ØBÉB1, B1ÉB2, …, Bn-1ÉBn, BnÉØA, из которой делается вывод (в силу транзитивности импликации) о справедливости теоремы ØB ÉØA. А в силу закона контрапозиции заключается о справедливости теоремы AÉB.

3. Доказательство приведением к абсурду.

Пусть требуется доказать истинность некоторого утверждения A. Предположим, что A ложно, тогда ØA - истинно, поскольку закон противоречия (X&ØXºЛ), имеющий место в логике высказываний, означает, что одновременно не могут быть истинными утверждение и его отрицание.

После этого показывается, что тогда имеется некоторое утверждение B такое, что истинными являются одновременно два утверждения: ØAÉB и ØAÉØB.[4]) Это и есть то, что называют абсурдом.

В логике высказываний тождественно-истинной является формула: (ØAÉB)&(ØAÉØB) ÉA (проверку чего мы предоставляем читателю).

Из этой формулы и (ØAÉB)&(ØAÉØB) по правилу вывода modus ponens следует, что имеет место утверждение A.

4. Доказательство необходимых и достаточных условий.

В математике часто встречаются теоремы вида: "Условие A равносильно условию В", что также выражается словами: "Для того, чтобы имело место условие А, необходимо и достаточно, чтобы выполнялось условие В". В виде формулы логики высказываний такая теорема может быть записана в виде: А~В. Доказательство ее обычно сводится к доказательству двух утверждений:

1. АÉВ (Если имеет место условие А, то выполняется и условие В)

2. ВÉА (Если имеет место условие В, то выполняется и условие А).[5])

Первое условие называют необходимым (то есть, В необходимо для А), а второе условие - достаточным (то есть, А достаточно для В). По-другому, первое называют прямой теоремой, а второе - обратной.

Доказательство и прямой, и обратной теорем может быть осуществлено любым из трех приведенных выше способов. После чего, можно утверждать и справедливость теоремы "Условие A равносильно условию В".

Существует и другой способ доказательства теорем вида: "Условие A равносильно условию В", когда одновременно доказывается необходимость и достаточность условия В для А. Для этого находится последовательность тождественно-истинных эквиваленций вида: A~A1, A1~A2,…,An-1~An, An~B, где A1,A2,A3,…,An - некоторые вспомогательные высказывания.

Отсюда делается вывод (в силу транзитивности эквиваленции) о справедливости теоремы A~B.

Наконец, доказательство теоремы вида A~B можно заменять доказательством равносильной ей противоположной теоремы ØА~ØВ. (В равносильности этих теорем легко убедиться с помощью таблиц истинности.)

Изложив основные структуры математических доказательств, мы надеемся, что читатель теперь по иному будет относиться к доказательству любой теоремы из курсов линейной алгебры, аналитической геометрии, математического анализа и т.д. Приступая к изучению доказательства любой теоремы, прежде всего, необходимо выяснить структуру доказательства, постараться отнести его к одному из рассмотренных четырех видов, а уже затем изучать само доказательство, четко представляя ту идею, которую применил автор теоремы для того, чтобы ее доказать.

 

Применение логики высказываний к анализу и синтезу

переключательных (контактных) схем

 

Переключательной (или контактной) схемой мы будем называть участок электрической цепи, включающий ряд переключателей (контактных выключателей), подобный приведенному на рис.2.2.

Рис.2.2. Вид переключательной схемы.

 

Каждому переключателю схемы сопоставим пропозициональную переменную Xi, которая будет принимать значение И (истина) или Л (ложь), если соответствующий переключатель замкнут или разомкнут (то есть, не проводит электрический ток).

Поскольку функция участка электрической цепи состоит в том, чтобы проводить электрический ток, то два участка, содержащие одни и те же переключатели и проводящие или не проводящие ток при одном и том же состоянии всех выключателей, мы будем считать "равными" и не различать между собой.

Легко сообразить, что участку цепи, представляющему собой последовательное соединение двух переключателей X1 и X2 будет отвечать формула логики высказываний, представляющая собой конъюнкцию пропозициональных переменных X1 и X2, то есть, X1&X2 (что означает, что такой участок проводит ток тогда и тогда, когда оба переключателя X1 и X2 замкнуты), а участку цепи, представляющему собой параллельное соединение двух переключателей X1 и X2 - формула, представляющая собой дизъюнкцию пропозициональных переменных X1 и X2, то есть, X1ÚX2. Сказанное представлено на рис. 2.3.

 

Рис. 2.3. Соответствие формул логики высказываний видам соединения переключателей.

 

Условимся обозначать через И всегда замкнутый контакт, а через Л - всегда разомкнутый. На схемах это будет выглядеть так, как представлено на рис. 2.4.

 

 

Рис.2.4. Соответствие логических констант всегда замкнутому и всегда разомкнутому контактам.

 

Условимся, наконец, обозначать через Xi и ØXi такую пару контактов, что когда контакт Xi замкнут, контакт ØXi обязательно разомкнут, и наоборот. Техническое осуществление такой пары контактов показано на рис.2.5.

 

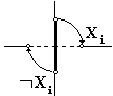
Рис.2.5. Реализация контактов Xi и ØXi.

 

Ясно, что параллельное и последовательное соединение переключательных схем обладает свойствами коммутативности, ассоциативности, идемпотентности.

Несколько сложнее проверяется выполнимость двух законов дистрибутивности:

Приведены попарно эквивалентные переключательные схемы, подтверждающие справедливость указанных законов дистрибутивности для переключательных схем.

Таким образом, все законы логики высказываний имеют аналоги в логике переключательных схем. Это, во-первых, позволяет моделировать сложные высказывания с помощью электрических цепей. Во-вторых, конструировать (синтезировать) переключательные схемы, удовлетворяющие наперед заданным условиям (которые могут быть и достаточно сложными).

 

Булевские функции

 

Многим из читателей, мы полагаем, приходилось иметь дело с так называемыми числовыми функциями: алгебраическими, тригонометрическими, логарифмическими и т.д. Все они характеризовались тем, что область определения и область значений функций представляли собой подмножества множества действительных чисел.

Например, функция y = f(x), задаваемая формулой y = sin(x) + 1, имеет в качестве области определения (обычно обозначается буквой Х) все множество действительных чисел, а в качестве области значений (чаще обозначаемой буквой Y) множество неотрицательных чисел, принадлежащих интервалу [0, 2]; функция y = j(x), задаваемая формулой j(x)=|lgx|+5, в качестве области определения имеет множество всех положительных действительных чисел, а в качестве области значений - множество положительных действительных чисел, больших 5.

Рассматриваемые нами здесь булевские (логические) функции характеризуются тем, что аргументы и сама функция принимают значения из множества логических констант {И, Л}.

В теории булевских функций чаще используются "числовые" эквиваленты логических констант: 1 вместо И, 0 - вместо Л. Ниже мы будем придерживаться именно этих обозначений.

Булевская функция в общем случае может содержать n аргументов: y=f(x1,x2,…,xn).

Как и математические функции, булевские функции могут задаваться: словесно, таблично или аналитически. Мы будем использовать последние два способа задания булевских функций: табличный (в виде таблиц истинности) и аналитический (в виде формул логики высказываний). Одна и та же функция может, естественно, задаваться по-разному.

Булевские функции одной переменной

Булевских функций от одной переменной всего 4. Эти функции и задающие их формулы логики высказываний приведены в следующей таблице:

 

x	0	1	Формулы логики высказываний, задающие функции
φ1	0	0	φ1(x) = 0 (константа 0)
φ2	0	1	φ2(x) = x (совпадает с переменной х)
φ3	1	0	φ3(x) = Øx (является отрицанием переменной х)
φ4	1	1	φ4(x) = 1 (константа 1)

 

Булевских функций от двух переменных всего насчитывается 16. Все они представлены в следующей таблице:

 

x	0	0	1	1	Формулы логики высказываний, задающие функции
y	0	1	0	1
f1	0	0	0	0	f1(x,y) = 0 (константа 0)
f2	0	0	0	1	f2(x,y) = x&y (конъюнкция)
f3	0	0	1	0	f3(x,y) = Ø(xÉy) (отрицание импликации)
f4	0	0	1	1	f4(x,y) = x (совпадает с переменной x)
f5	0	1	0	0	f5(x,y) = Ø(yÉx) (отрицание обратной импликации)
f6	0	1	0	1	f6(x,y) = y (совпадает с переменной y)
f7	0	1	1	0	f7(x,y) = xÅy (строгая дизъюнкция)
f8	0	1	1	1	f8(x,y) = xÚy (дизъюнкция)
f9	1	0	0	0	f9(x,y) = Øx&Øy (конъюнкция отрицаний)
f10	1	0	0	1	f10(x,y) = x~y (эквиваленция)
f11	1	0	1	0	f11(x,y) = Øy (отрицание y)
f12	1	0	1	1	f12(x,y) = yÉx (обратная импликация)
f13	1	1	0	0	f13(x,y) = Øx (отрицание x)
f14	1	1	0	1	f14(x,y) = xÉy (импликация)
f15	1	1	1	0	f15(x,y) = Ø(x&y) (отрицание конъюнкции)
f16	1	1	1	1	f16(x,y) = 1 (константа 1)

Естественно, многие из перечисленных функций могут быть заданы другими, но равносильными формулами логики высказываний.

 

Булевские функции n переменных

 

Областью определения такой булевской функции будет n-тая декартова степень множества {0,1}, то есть всевозможные двоичные наборы длины n вида <a1a2…an>, где aiÎ{0,1}. Число таких всевозможных наборов (n-ок) составляет 2n.

Область значений булевской функции от n переменных - это множество {0,1}.

В дальнейшем мы будем рассматривать только всюду определенные булевские функции, то есть область определения таких функций совпадает с n-той декартовой степенью множества {0,1}.

Булевские функции от большего числа переменных могут быть так же заданы таблично, или с помощью формул логики высказываний, или в виде суперпозиции (взаимной подстановки) булевских функций одной и/или двух переменных.

Например, булевская функция y=f(x,y,z), задаваемая формулой логики высказываний x&y Ú Øx&Øy Ú z может быть задана в виде следующей суперпозиции функций от одной и двух переменных: y=f8(f8(f2(x,y),f9(x,y)),φ2(z)).

Учитывая принципиальную возможность выразить булевскую функцию от любого числа переменных в виде суперпозиции (взаимной подстановки) булевских функций от одной и двух переменных, мы чаще будем использовать либо табличный способ задания таких функций, либо с помощью формул логики высказываний.

Табличный способ задания булевских функций от одной и двух переменных (см. приведенные выше таблицы, определяющие эти функции) наводит нас на некоторые соображения:

- число наборов истинностных значений, на которых определена булевская функция от n переменных, составляет 2n (при n=1 это число составляет 2, при n=2 - 4);

- значение каждой булевской функции от n переменных представляет собой двоичный набор длины 2n;

- каждая булевская функция отличается от любой другой булевской функции с тем же числом переменных своим значением хотя бы на одном из таких наборов

А отсюда можно сделать предположение о том, число N различных булевских функций от n переменных равно числу различных двоичных наборов длины 2n, то есть: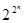

При n=1 это число равно 4, при n=2 - 16, n=3 - 256, n=4 - 65536 и т.д.

 

Полные системы булевских функций

 

В предыдущем пункте было отмечено, что можно выразить любую булевскую функцию от n переменных в виде суперпозиции (взаимной подстановки) булевских функций от одной и двух переменных. В свою очередь эти функции задаются формулами, содержащими логические операции: отрицание(Ø), конъюнкцию (&),строгую дизъюнкцию (Å), дизъюнкцию(Ú), импликацию(É), эквиваленцию (~).

Но как известно из логики высказываний, операции логики высказываний строгая дизъюнкция (Å), импликация (É), эквиваленция (~) могут быть выражены через дизъюнкцию (Ú), конъюнкцию (&) и отрицание (Ø).

В свою очередь, дизъюнкция (Ú) может быть выражена через конъюнкцию (&) и отрицание (Ø), а конъюнкция (&) - через дизъюнкцию (Ú) и отрицание (Ø).

Таким образом, конъюнкция и отрицание, а также дизъюнкция и отрицание, образуют полную систему логических связок, то есть через эти операции могут быть выражены все остальные.

Более того, можно определить логическую операцию, через которую выражаются все шесть операций: отрицание (Ø), конъюнкция (&), дизъюнкция (Ú), строгая дизъюнкция (Å), импликация (É), эквиваленция (~). Таковой, например, является операция, соответствующая сложному союзу "не А или не В" ("или" соединительное). Эта операция обозначается символом ô(например, АôВ) и получила название штрих Шеффера. Штрих Шеффера определяется с помощью следующей таблицы:

 

X	Y	XôY
Л	Л	И
Л	И	И
И	Л	И
И	И	Л

 

Как легко видеть, штрих Шеффера представляет собой отрицание конъюнкции: XôY º ØXÚØY º Ø(X&Y).

Можно убедиться, что ØX º XôX.

А отсюда: X&Y º Ø(XôY) º (XôY) ô(XôY).

Таким образом, через штрих Шеффера могут быть выражены конъюнкция и отрицание, а значит и все остальные операции логики высказываний. То есть система логических связок, содержащая единственную операцию - штрих Шеффера, является полной.

Есть еще одна логическая операция, аналогичная штриху Шеффера и называемая стрелкой Пирса. Она обозначается символом ­ и представляет собой отрицание дизъюнкции (или конъюнкцию отрицаний): X­Y º Ø(XÚY) º ØX&ØY.

Можно убедиться, что ØX º X­X.

А отсюда: XÚY º Ø(X­Y) º (X­Y) ­ (X­Y).

Таким образом, через стрелку Пирса могут быть выражены дизъюнкция и отрицание, а значит и все остальные операции логики высказываний. То есть система логических связок, содержащая единственную операцию - стрелку Пирса, является полной.

Систему булевских функций будем называть функционально полной, если любую булевскую функцию можно выразить в виде суперпозиции (взаимной подстановки) функций из этой системы.

В соответствии с высказанными выше соображениями о полноте системы логических связок и задании булевских функций формулами логики высказываний, можно сделать вывод о функциональной полноте следующих систем булевских функций:

S0 = {φ3(x), f2(x,y), f8(x,y)} - отрицание, конъюнкция, дизъюнкция.

S1 = {φ3(x), f2(x,y)} - отрицание, конъюнкция.

S2 = {φ3(x), f8(x,y)} - отрицание, дизъюнкция.

S3 = {f15(x,y)} - отрицание конъюнкции (штрих Шеффера).

S4 = {f9(x,y)} - отрицание дизъюнкции (стрелка Пирса).

S5 = {φ3(x), f14(x,y)} - отрицание, импликация.

В последующем мы увидим, что с точки зрения проектирования вычислительных устройств особый интерес представляют S3 и S4.

Общий критерий функциональной полноты системы булевских функций, выражающий необходимые и достаточные условия, носит название критерия Поста-Яблонского.[6] Его изложение выходит, к сожалению, за рамки настоящего пособия.

 

123	Поделиться:

Воспользуйтесь поиском по сайту: