 |
Методический инструментарий оценки стоимости денег во времени.
|
|
|
|
Смысл операций по учету временного фактора заключается в приведении разных по времени и периодичности денежных потоков к одинаковому моменту времени с помощью методов начисления процентов или дисконтирования. Это необходимо в силу того, что с экономической точки зрения бессмысленно напрямую (без приведения к одному временному периоду) сопоставлять денежные суммы, полученные в разное время. Для приведения разновременных денежных потоков в сопоставимый вид в качестве момента времени может выступать:
à настоящее время, когда предполагается приведение будущих денежных потоков к настоящему времени. Эта процедура называется дисконтированием, а полученная в результате дисконтирования сумма – современной стоимостью денежных средств;
à будущее время, когда предполагается оценка стоимости текущих вложений и вызванных ими денежных потоков в определенный момент в будущем. Эта процедура называется наращением или компаудингом, а получаемая сумма - наращенной или будущей стоимостью.
Таким образом, с позиции временной ценности, обобщающими характеристиками денежных потоков являются наращенная сумма и современная стоимость.
Под современной (дисконтированной) стоимостью денежных средств понимают текущую, “сегодняшнюю” стоимость будущих денежных сумм, дисконтированных на начало срока финансовой операции или некоторый упреждающий момент времени.
В основе определения дисконтированной стоимости лежит понимание временного предпочтения в распоряжении денежными средствами или, по-другому, понимание стоимости денег во времени. Текущее распоряжение ресурсами позволяет предпринимать действия, которые с течением времени приведут к росту будущего дохода. Поэтому стоимость денежных средств будет определяться возможностью получения дополнительного дохода от более раннего вложения средств.
|
|
|
Количественным выражением временного предпочтения в использовании денежных средств в данной экономической ситуации обычно выступают процентные ставки, характеризующие уровень доходности того или иного финансового инструмента.
Экономический смысл процесса дисконтирования состоит в нахождении суммы, эквивалентной будущей стоимости денежных средств. Эквивалентность будущих и текущих денежных сумм означает, что инвестору должно быть безразлично, иметь ли сегодня некоторую сумму денежных средств или получить через определенный период времени ту же сумму, но увеличенную на величину начисленных за период процентов. Именно в этом случае временного безразличия можно говорить о том, что найдена современная стоимость денежных ресурсов, которые будут получены в будущем. При осуществлении операций дисконтирования движение денежного потока идет от будущего к настоящему.
Наращенная (будущая) стоимость – это стоимость, которая будет получена в будущем в результате вложения денежных средств в какой-либо финансовый актив или в результате инвестирования при определенных условиях (ставке доходности, временном периоде, условиях начисления процентов и др.), рассчитываемая как сумма первоначального капитала с начисленными на нее к концу срока процентами.
Можно сказать, что наращением называют процесс увеличения исходной суммы денег в связи с присоединением к ней процентов в результате проведения финансовой операции.
Например, при вложении денег в банк в виде вклада, вкладчик рассчитывает на получение определенного дохода, обусловленного установленной доходностью и сроком договора. Проценты по вкладу в зависимости от договоренности сторон могут выплачиваться вкладчику по мере их начисления, либо присоединяться ко вкладу. Во втором случае и имеет место процесс наращения.
|
|
|
В случае осуществления процесса наращения рассматривается движение денежного потока от настоящего к будущему, при этом известными величинами являются исходная сумма, ставка процента и срок, т.е. период начисления.
Результативность финансовых операций характеризуется такими основными параметрами как:
à процент – абсолютная сумма дохода от предоставления капитала в долг или плата за пользование ссудным капиталом во всех его формах. Выражается в денежных единицах, как за весь срок финансовой операции, так и в годовом измерении;
à ставка доходности – относительный показатель, характеризующий сумму дохода, полученного с вложенного капитала. Выражается в виде десятичной дроби или в процентах в годовом измерении.
В зависимости от метода расчета относительная доходность может выражаться в виде процентной и учетной ставки:
à процентная ставка (ставка процента) – относительный показатель, в соответствие с которым в установленные сроки выплачивается сумма процента в расчете на единицу вложенного (первоначального) капитала. Обычно процентная ставка характеризуется отношением годовой суммы процента и суммы предоставленного (заимствованного) капитала, выраженным десятичной дробью или процентом.
à учетная ставка (дисконт) - относительный показатель, в соответствие с которым сумма процента в расчете на единицу капитала удерживается с суммы, подлежащей уплате в конце периода. Учетная ставка характеризуется отношением годовой суммы процента и суммы подлежащего к уплате капитала, выраженным десятичной дробью или процентом.
При исчислении доходности финансовых активов в финансовых расчетах используют два основных метода начисления процентов в зависимости от базы начисления – простой и сложный.
Простой процент – метод начисления процентов, при котором на сумму дохода, начисляемого к основной сумме капитала в каждом интервале, дальнейшие расчеты платежей не осуществляются.
Сложный процент – метод начисления процентов, при котором сумма дохода, начисляемого в каждом интервале, не выплачивается, а присоединяется к основной сумме капитала и в последующем платежном периоде сама приносит доход. Начисление сложного процента применяется, как правило, при долгосрочных финансовых операциях (инвестировании, кредитовании и т.п.).
|
|
|
Введем основные условные обозначения, используемые в финансовых расчетах:
Р – первоначальная (современная) стоимость капитала,
F – наращенная (конечная) стоимость капитала,
I – процентный доход (абсолютная сумма процента),
r – простая процентная ставка,
d – простая учетная ставка,
rс – сложная процентная ставка,
dс – сложная учетная ставка,
n – срок финансовой операции,
к – количество внутригодовых начислений процентов.
Простейшим видом финансовой сделки является однократное предоставления в долг некоторой суммы Р с условием, что через какое-то время n будет возвращена большая сумма F.
Тогда процентная и учетная ставки методом простых процентов будут определены соответственно:
годовая простая процентная ставка годовая простая учетная ставка
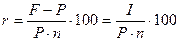

Эти показатели взаимосвязаны между собой:


Различия в этих формулах состоит в том, что в первом случае (процентная ставка) за базу сравнения берется исходная величина, а во втором (учетная ставка) – возвращаемая сумма.
Пример: Банк выдает кредит в размере 100 тыс. руб. на 1 год под 10% годовых. Если применяется процентная ставка, то заемщик получит на руки 100 тыс., а должен будет вернуть через год 110 тыс. (100+100*10%/100). Если используется учетная ставка и сумма процентов удерживается сразу, то заемщик получит на руки 90 тыс., а должен будет вернуть 100тыс. (90+100*10%/100).
При определении наращенной и приведенной стоимости денежных потоков может быть использована как процентная, так и учетная ставки процента.
Оценка стоимости денег во времени, как мы отмечали, может выполняться в рамках решения двух задач:
а) прямой, т.е. проводится оценка с позиции будущего (реализуется схема наращения);
б) обратной, т.е. проводится оценка с позиции настоящего (реализуется схема дисконтирования).
|
|
|
Для оценки простейшего денежного потока, состоящего из одного члена (некоторой единичной денежной суммы) применяются следующие алгоритмы.
Прямая задача предполагает оценку первоначальной суммы на некоторый момент в будущем, т.е. в её основе лежит будущая стоимость. Формула наращенной стоимости может быть определена на базе простых или сложных процентов:
а) простые проценты б) сложные проценты
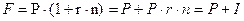



Пример: Какова будет стоимость вклада через 5 лет, первоначальная стоимость которого 1000 руб., если на него ежегодно начисляются проценты по ставке 10 % годовых. Применяя различные способы исчисления процентов, получим:
F = 1000*(1+5*0,1) = 1500 – по простым процентам
F=1000*(1+0,1)5=1610,5 – по сложным процентам
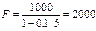 - по простому дисконту
- по простому дисконту
 - по сложному дисконту
- по сложному дисконту
Норма доходности r(d) представляет собой вознаграждение, которое требует инвестор за отсрочку платежей или отражает доходность альтернативных финансовых вложений. Использование в расчетах сложного процента в случае многократного его начисления более корректно, поскольку в этом случае капитал, генерирующий доходность, постоянно возрастает. Поэтому в большинстве финансовых операциях используется именно метод сложных процентов.
Формула сложных процентов является базовой в финансовых вычислениях, поэтому множитель (1+rс)n = FM1, называемый мультиплицирующим множителем и обеспечивающий наращение стоимости, табулирован. Его значения задаются в зависимости от ставки доходности (r) и срока сделки (n) - FM1(r;n) (см. приложение 1).
Экономический смысл мультиплицирующего множителя FM1 состоит в том, что он показывает, чему будет равна одна денежная единица через n периодов при заданной процентной ставке r.
Для учетной ставки множитель наращения равен: FM1 = 
Обратная задача предполагает оценку дисконтированной (приведенной) денежной суммы с позиции настоящего, что осуществляется с помощью формулы дисконтированной стоимости:
а) простые проценты б) сложные проценты

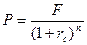


Основной посылкой в рассматриваемых алгоритмах служит предпосылка, что анализ ведется с позиции разумного инвестора, т.е. инвестора, не накапливающего полученные денежные средства в “чулке”, а немедленно инвестирующего их с целью получения дополнительного дохода. Именно этим и объясняется, что при оценке потоков, как при дисконтировании, так и при наращении, предполагается капитализация по схеме сложных процентов.
Величину 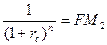 (FM2=(1-dс)n – для учетной ставки) называют коэффициентом дисконтирования или дисконтирующим множителем, который показывает “сегодняшнюю” цену одной денежной единицы будущего, т.е. чему с позиции текущего момента равна одна денежная единица, циркулирующая в сфере бизнеса n периодов спустя от момента расчета при заданной доходности r и частоте начисления процентов.
(FM2=(1-dс)n – для учетной ставки) называют коэффициентом дисконтирования или дисконтирующим множителем, который показывает “сегодняшнюю” цену одной денежной единицы будущего, т.е. чему с позиции текущего момента равна одна денежная единица, циркулирующая в сфере бизнеса n периодов спустя от момента расчета при заданной доходности r и частоте начисления процентов.
|
|
|
При использовании названных формул следует помнить ряд принципов, на которых они основаны:
à во-первых, доходность принято измерять годовым интервалом. Т.о., в формулах применяется годовая ставка, т.е. подразумевается годовое начисление процентов;
à во-вторых, единицы времени, в которых измеряется доходность и период упреждения должны совпадать, т.е., если используется годовая ставка процента, то временной период также должен быть выражен в годах. Если период выражен в месяцах, то следует использовать месячную ставку процента.
Если предполагается, что начисление процентов (или дисконтирование) будет производиться чаще, чем один раз в год (т.е. к-раз), формулы будущей или дисконтированной стоимости преобразуется таким образом, что годовая ставка делится на число периодов начисления в году, а число лет умножается на число периодов в году (данный алгоритм применяется только для сложных процентов):


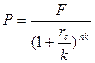

где к – число периодов начисления (интервалов дисконтирования) в одном году. Например, при ежемесячном начислении процентов, к=12.
На основе вышеприведенных формул, можно вывести формулы для расчета срока финансовой операции и ее доходности.
а) для процентных ставок б) для учетных ставок
срок сделки
простые проценты 

сложные проценты 
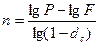
ставки доходности
простые проценты 

сложные проценты 

|
|
|


