 |
Определение угла фазового сдвига
|
|
|
|
Измерение ёмкостей и индуктивностей с помощью электронного осциллографа
(Лабораторная работа № 5)
Цель работа – ознакомление с теорией и практикой метода измерения ёмкостей и индуктивностей путём определения фазовых сдвигов с помощью электронного осциллографа.
Краткое изложение теории
Как и при измерении ёмкостей и индуктивностей методом моста переменного тока, в основе метода измерения ёмкостей и индуктивностей путём определения фазового сдвига лежит рассмотрение режимов работы цепей гармонического переменного тока, включающих в себя реактивные элементы (ёмкости и индуктивности. В целом данный метод относится к методам косвенных измерений.
Углы фазового сдвига
При описании работы цепей переменного тока, включающих в себя источник напряжения синусоидальной (гармонической) формы и реактивные элементы, широко применяется метод комплексных амплитуд (подробное описание сущности метода приведено в прилож. 1 к данному сборнику), позволяющий исключить сложные преобразования тригонометрических функций временного аргумента. В общем виде цепи переменного тока, включающие в себя неизвестные реактивные элементы, имеют следующий вид:

Рис. 1. Схемы цепей переменного тока:
А – общий вид цепи переменного тока;
Б – цепь переменного тока, включающая реальный конденсатор;
В – цепь переменного тока, включающая реальную катушку индуктивности
Во всех вариантах схемы присутствует генератор гармонического напряжения (G на рис. 1). В качестве нагрузки генератору G выступает:
а) в общем случае некоторый набор из активных и реактивных элементов, эквивалентный импеданс которого можно описать следующим комплексным числом:
|
|
|
 , (1)
, (1)
где Rx –‘эквивалентное активное сопротивление всех элементов цепи;
Xx – эквивалентное реактивное сопротивление всех элементов цепи;
б) в случае включения в цепь только лишь реального конденсатора (или конденсаторов) схема принимает вид, представленный на рис.1,б, а импеданс цепи будет описываться следующей формулой:

 ;
;
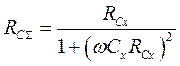 ;
;
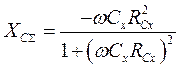 , (2)
, (2)
где Сx – ёмкость конденсатора;
ω – рабочая круговая частота напряжения, приложенного к цепи (ω=2πf);
RCx – активное сопротивление конденсатора, включающее в себя сопротивление неидеального диэлектрика, заполняющего конденсатор, и сопротивление, обусловленное поляризацией полярного диэлектрика;
RCΣ – эквивалентное активное сопротивление цепи;
XCΣ – эквивалентное реактивное сопротивление цепи;
в) в случае включения в цепь только лишь реальной катушки индуктивности (или катушек) схема принимает вид, представленный на рис. 1,в, а импеданс цепи описывается следующей формулой:
 , (3)
, (3)
где RLx – активное сопротивление проводов, из которых намотана катушка, и всех соединительных проводов;
XLx=ωLx – реактивное сопротивление катушки;
Lx – индуктивность катушки.
Обобщая выражения (1) – (3), можно сделать вывод, что импеданс цепи переменного тока имеет комплексный характер. В таком случае между синусоидальным током i, протекающим в цепи
 , (4)
, (4)
и синусоидальным напряжением u, падающем на элементах цепи
 , (5)
, (5)
будет наблюдаться фазовый сдвиг φ, который можно определить по формуле:
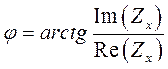 . (6)
. (6)
В случае реализации схемы рис. 1,б имеем:
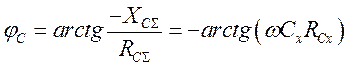 . (7)
. (7)
В случае реализации схемы рис. 1,в имеем:
 . (8)
. (8)
Угол фазового сдвига может быть равным от 0 до π/2 рад. по модулю. Иллюстрацией выражений (7) и (8) служат векторные диаграммы в плоскости комплексного числа (рис. 2).

Рис. 2. Векторные диаграммы токов, напряжений и импедансов в цепях переменного тока:
А – для цепей с конденсаторами;
|
|
|
Б – для цепей с катушками индуктивности
Таким образом, угол фазового сдвига между током и напряжением в цепи переменного тока несёт в себе в неявной форме информацию об электрических параметрах всех элементов цепи.
Определение угла фазового сдвига
Одним из наиболее простых методов определения угла фазового сдвига между двумя гармоническими по форме сигналами является метод фигур Лиссажу: если два гармонических и взаимно перпендикулярных сигала подать на некий материальны объект, то он под действием этих сигналов станет описывать в пространстве интерференционные фигуры, названные фигурами Лиссажу. Форма фигур зависит от соотношения амплитуд и разности фаз между сигналами (см. табл. в п. 3.2.1.4.4 лабораторной работы № 2).
Наиболее просто фигуры Лиссажу можно получить на экране электронного осциллографа. Для этого его следует перевести в режим работы с двумя входами и подать на эти входы взаимно перпендикулярные гармонические напряжения, имеющие угол фазового сдвига φ:
 .
.
Так как в реальной цепи переменного тока угол фазового сдвига наблюдается между током i (выражение (4)) и напряжением u (выражение (5)), то в качестве напряжения uY будет выступать напряжение, падающее на элементе цепи, а в качестве напряжения uX будет выступать напряжение, пропорциональное току:
 , (9)
, (9)
где Ro – специальное токовое измерительное сопротивление известного номинала, включаемое последовательно с измеряемым элементом цепи. Величина номинала измерительного резистора Ro выбирается относительно небольшой, чтобы не менять существенно электрические режимы работы цепи (в настоящей работе выбрано Ro=10 Ом, которое установлено на лабораторном стенде). В этом случае измерительная схема лабораторной установки будет иметь следующий вид:

Рис. 3. Рабочая схема лабораторной установки:
Ro – измерительный токовый резистор номиналом 10 Ом;
Zx – измеряемый элемент схемы (конденсатор или катушка индуктивности);
PV – двухканальный электронный осциллограф;
G – генератор синусоидальных напряжений
При этом на экране осциллографа будут наблюдаться одновременно напряжения: uX и uY. Напряжения UXm и UYm, входящие в выражения этих напряжений, – это амплитуды смещения луча на экране осциллографа.
|
|
|
 . (10)
. (10)
Это – формула эллипса. То есть, луч на экране будет описывать фигуру в виде эллипса, ориентация и форма которого зависят от искомого угла φ от коэффициентов усиления по каналам осциллографа X и Y (см. рис. 4).
Если эллипс расположен длинной осью сверху–вниз и справа–налево (в 1–3 квадрантах), то φ>0, если эллипс расположен длинной осью сверху–вниз и слева–направо (в 2–4 квадрантах), то φ<0.
Усиление по каналам X и Y всегда можно подобрать так, чтобы амплитуда отклонения луча по осям x и y на экране осциллографа были равны, то есть:
 . (11)
. (11)
Тогда эллипс на экране будет вписан в квадрат, его наклон к координатным осям составит угол β=45о (см. рис. 4), а уравнение (10) примет вид:
 . (12)
. (12)

Рис. 4. Изображение на экране осциллографа
В системе координат  , повёрнутой относительно исходной на угол β=450 по формулам преобразования
, повёрнутой относительно исходной на угол β=450 по формулам преобразования


получим уравнение эллипса в канонической форме:
 , (13)
, (13)
где a и b – полуоси эллипса (b≥a):
 . (14)
. (14)
Откуда получаем искомый угол фазового сдвига:
 . (15)
. (15)
Знак угла фазового сдвига φ можно определить лишь по положению эллипса на экране осциллографа (см. рис.4).
|
|
|


