 |
Построить аналитическую амплитудно-фазовую частотную характеристику звена, эквивалентирующего нагрузку.
|
|
|
|
Курсовой проект по курсу
«Теория автоматического регулирования»
Выполнили:
Студенты группы
43212/1
Дорохов Д.А.
Петелин С.Д.
Проверил:
Попков Е.Н.
Санкт-Петербург
Представить нагрузку системы питания в виде звена, для которого входным сигналом является напряжение на зажимах источника питания, а выходным сигналом – указанная регулируемая переменная. Получить описание звена в виде сокращенной записи дифференциального уравнения и передаточной функции. Установить тип звена и рассчитать численные значения параметров.
Исходная схема:
Параметры нагрузки:
Получим описание звена в виде передаточной функции:
Передаточная функция – это отношения изображения выходного сигнала к изображению входного 
.
Перейдём в операторное пространство (нулевые н.у., 
За изображение входного сигнала примем 
:
За изображение выходного сигнала примем ток резистора 
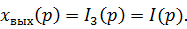
Следовательно необходимо найти:
Найдем 
:
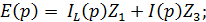
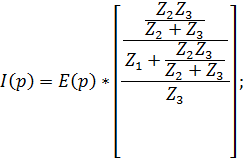
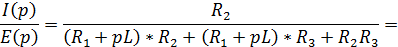
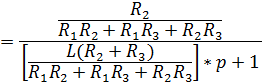
| Конечное выражение имеет вид: |
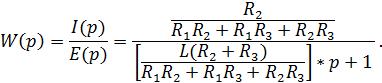
Найдем описание звена в виде сокращенной записи дифференциального уравнения – это отношения полинома при воздействии к полиному при реакции 
.
Составим систему уравнений:
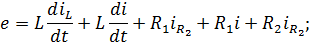
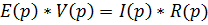
Передаточная функция и сокращенная форма записи дифференциального уравнения совпадают.
По передаточной функции можем определить тип: инерционное звено первого порядка, имеющее общий вид:
Рассчитаем численные значения параметров:
2. Определить двумя способами величину э.д.с. Е0 основного источника:
1) методом расчета установившегося режима системы питания и нагрузки;
2) используя передаточную функцию звена нагрузки. Э.Д.С. регулируемого источника Ер в установившемся режиме принять равной нулю.
|
|
|
Сначала определим ЭДС основного источника с помощью расчета установившегося режима.
Исходная схема:
В установившемся режиме ω=0, а сопротивление катушки определяется как 
. Следовательно, в установившемся режиме сопротивление катушки равно 0.
Определим ЭДС основного источника с помощью передаточной функции:
В установившемся режиме 
тогда изображение тока будет иметь вид: 
Т.к. данного изображения нет в таблице, то воспользуемся теоремой разложения:
Тогда E(p) можно представить в виде:
Оригинал:
Построить аналитическую переходную характеристику звена, эквивалентирующего нагрузку
Переходная характеристика звена представляет собой реакцию на выходе звена, вызванную подачей на его вход единичного ступенчатого воздействия, т.е. воздействие, которое мгновенно возрастает от нуля до единицы и далее остается неизменным.
Переходная характеристика звена 
для нашего звена имеет вид:
)
)
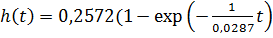при 
- переходный процесс завершится
при 
, что составляет 98% от 
.
Подготовить имитационную модель и получить на ЭВМ переходную характеристику звена, эквивалентирующего нагрузку. Сравнить с результатами выполнения п.3. Определить параметры звена по экспериментальной переходной характеристике.
Подготовим имитационную модель. В нее войдут следующие блоки: генератор кусочно-постоянного сигнала, инерционное звено первого порядка, эквивалентирующее нагрузку, табулятор и осциллограф.
Схема модели в программе РИТМ:
BLT103 – генератор кусочно-постоянного сигнала
BLT133 – инерционное звено первого порядка
BLT014 – осциллограф
BLT015 – табулятор
Выведем два сигнала: 101 – сигнал с выхода генератора, 201 – сигнал с выхода инерционного звена.
Используя данные табулятора найдем экспериментальные значения K и Т.
|
|
|
hуст=0,2572=K
При t1=0,022 (c) h(0,022)=0,137131
Используя формулу 
найдем Т:
(c)
Сравним экспериментальные данные с теоретическими:
| Определение | K | T |
| Теоретическое | 0,2572 | 0,0287 |
| Экспериментальное | 0,2572 | 0,02888 |
| Погрешность, % | 0,62 |
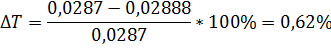
5. Выполнить тестовый расчет, подтверждающий правильность определения величины э.д.с. Е0
Расчет выполним, используя ту же имитационную модель, что и в п.4. Изменим только величину выходного сигнала генератора кусочно-постоянного сигнала. Вместо 1 установим рассчитанное значение ЭДС 388,8 В. В установившемся режиме величина регулируемой переменной, сигнала 202 с выхода звена нагрузки, должна соответствовать заданному значению.
Из таблиц мгновенных значений:
х 101=388,8
х 202уст=99,9993
Необходимое значение величины регулируемой переменной:
х 202уст =100
| Определение | х 202уст |
| Теоретическое | |
| Экспериментальное | 99,9993 |
| Погрешность, % | 0,0007 |
Погрешность очень низкая, что говорит о высокой точности определения E0
Построить аналитическую амплитудно-фазовую частотную характеристику звена, эквивалентирующего нагрузку.
Передаточная функция звена:
Получим:
Построим годограф амплитудно-фазовой частотной характеристики:
Выберем на годографе 7 точек:
| № | W’ | W’’ |
| 0,246946 | -0,05032 | |
| 0,223629 | -0,086645 | |
| 0,184843 | -0,11565 | |
| 0,128391 | -0,1286 | |
| 0,0754079 | -0,11708 | |
| 0,0386144 | -0,091872 | |
| 0,0111603 | -0,052401 |
Решение обратной задачи:
Выразим ω:
Теперь зная 
найдем W’ и W’’:
| № | , рад/с
| W’ | W’’ |
| 7,0999737 | 0,24694632 | -0,05032006 | |
| 13,49999127 | 0,22362936 | -0,08664514 | |
| 21,80021275 | 0,18484208 | -0,11564942 | |
| 34,89992474 | 0,12839083 | -0,12859983 | |
| 54,09834392 | 0,07541114 | -0,11708504 | |
| 82,89951372 | 0,03861474 | -0,09187281 | |
| 163,59943866 | 0,01116035 | -0,05240122 |
Построим годограф:
Подготовить имитационную модель и провести серию расчетов, позволяющую построить экспериментальную амплитудно-фазовую частотную характеристику звена, эквивалентирующего нагрузку. Сравнить с результатами выполнения п.6.
Заполним таблицу, с данными необходимыми для проведения экспериментов:
| № | ω, рад/с | f, Гц | Т, с | Туст, с | Ток, с | h, c |
| 7,0999737 | 1,12999591 | 0,88495896 | 4,42 | 8,85 | 0,00885 | |
| 13,49999127 | 2,14959034 | 0,46542143 | 2,33 | 4,65 | 0,00465 | |
| 21,80021275 | 3,46961162 | 0,2882167 | 1,44 | 2,88 | 0,00288 | |
| 34,89992474 | 5,55449554 | 0,18003435 | 0,90 | 1,80 | 0,00180 | |
| 54,09834392 | 8,61001885 | 0,11614376 | 0,58 | 1,16 | 0,00116 | |
| 82,89951372 | 13,19386739 | 0,08579279 | 0,38 | 0,76 | 0,00076 | |
| 163,59943866 | 26,03765935 | 0,03840591 | 0,19 | 0,38 | 0,00038 |
|
|
|
ω возьмем из п.6.
Частота:
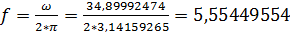(Гц)
Период:
Время установившегося сигнала:
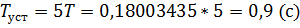
Время окончания расчета:
Шаг расчета:
В эксперименте будем использовать следующую модель:
BLT091 – генератор гармонического сигнала
BLT133 – инерционное звено первого порядка
BLT014 – осциллограф
BLT015 – табулятор
В эксперименте будем подавать на вход нашего звена гармонический сигнал с амплитудой равной 1 и различной частотой.
Проведя серию опытов, получим следующие результаты:
| № | Xmi | φi , рад | W’ | W’’ |
| 0,25202 | -0,201003 | 0,24694604 | -0,05031636 | |
| 0,239822 | -0,369696 | 0,22361896 | -0,08665536 | |
| 0,218067 | -0,558909 | 0,18488465 | -0,11563254 | |
| 0,181705 | -0,786292 | 0,12836994 | -0,12859963 | |
| 0,139252 | -0,998674 | 0,07539349 | -0,11707665 | |
| 0,0996545 | -1,17288 | 0,03861595 | -0,09186854 | |
| 0,0537129 | -1,3585 | 0,01131759 | -0,05250703 |
Xmi – амплитуда сигнала 201 с выхода инерционного звена
φi – фаза сигнала 201 с выхода инерционного звена
Пример, осциллограммы сигналов 101 и 201 для 4 опыта
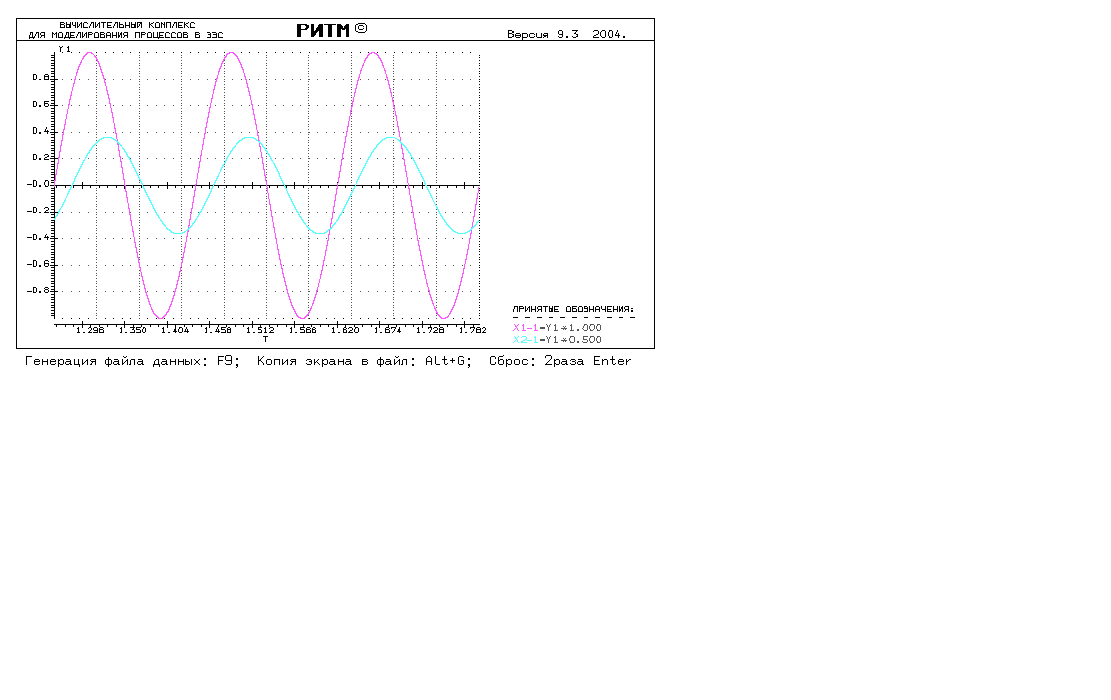
Значения Xmi и φi определяют точки в полярных координатах. Для перехода к прямоугольным координатам W’ и W” воспользуемся следующими формулами:
Построим экспериментальный годограф:
Теоретический и экспериментальный годографы совпадают, что говорит о правильности проведенных экспериментов.
|
|
|
