 |
Составить структурно-алгоритмическую схему системы автоматического управления.
|
|
|
|
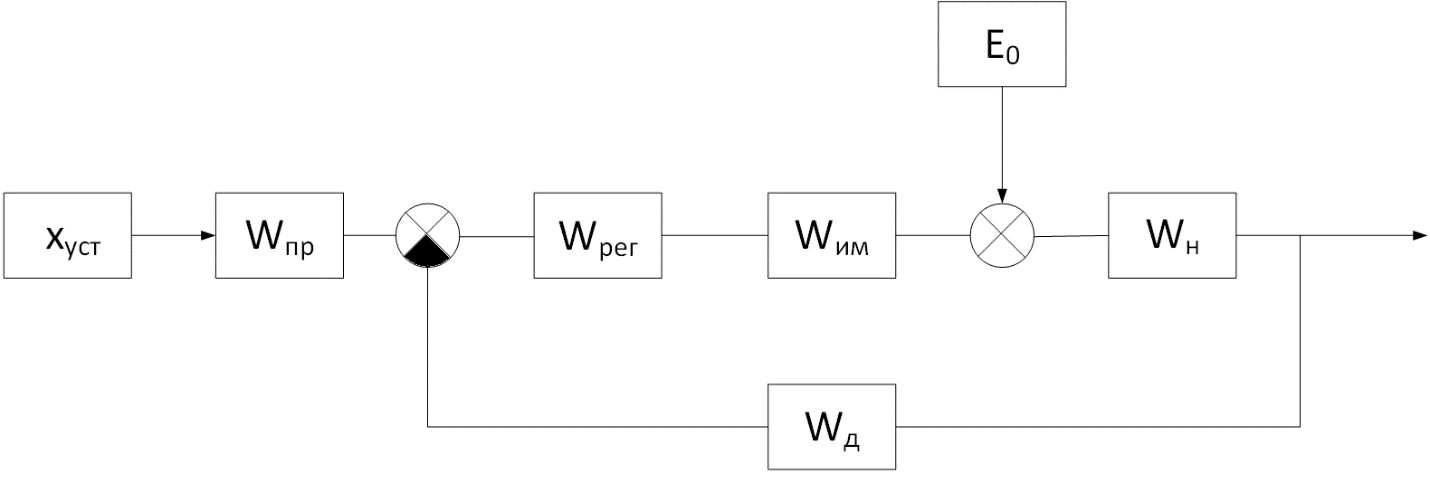
Исходная схема автоматического управления имеет вид:
Выполним преобразования схемы, чтобы найти эквивалентные передаточные функции относительно сигнала основного источника и сигнала уставки.
Перенос сумматора:
Объединение звеньев:
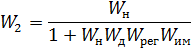
Эквивалентная передаточная функция относительно E0:
Эквивалентная передаточная функция относительно хуст:
9. Построить область устойчивости системы в плоскости коэффициентов Кр и Кд, где Кр – коэффициент передачи звена, эквивалентирующего регулятор, а Кд – коэффициент передачи звена, эквивалентирующего датчик текущего значения регулируемой переменной.
Эквивалентная передаточная функция:
Подставим значения известных параметров:
Характеристический полином:
Границы устойчивости определим из причин нарушения устойчивости:
1) Появление нулевого вещественного корня:
2) Появление бесконечного корня:
3) Равенство нулю предпоследнего минора матрицы Гурвица:
Матрица Гурвица:
Предпоследний минор:
Получим, что границы устойчивости определятся следующими уравнениями:
1) 
2) 
Построим границы устойчивости:
Имеем 5 областей. По критерию Гурвица проверим области на устойчивость. Определитель матрицы Гурвица и все ее диагональные миноры должны быть положительны.
|
|
|
1 область:
|
|
2 область:
|
|
3 область:
|
|
4 область:
|
|
5 область:
|
|
Следовательно, областью устойчивости является область 5
10. Подготовить имитационную модель системы автоматического управления. Выполнить моделирование процесса включения системы питания при нулевых начальных условиях для заданных преподавателем величин коэффициентов Кр и Кд.
|
|
|
Структурно-алгоритмическая схема САУ имеет вид:
Модель в программном комплексе РИТМ будет иметь следующий вид:
BLT103 – генератор кусочно-постоянного сигнала (
и 
)
BLT135 – сумматор
BLT133 – инерционное звено I-ого порядка (регулятор, исполнительный механизм, нагрузка)
BLT089 – пропорциональное звено (датчик)
BLT014 – осциллограф
BLT015 – табулятор
Выполним моделирование процесса включения при нулевых начальных условиях.
К р=2 К д=4
Из осциллограммы в п.10 видно, что в установившемся режиме величина ЭДС регулируемого источника не равна нулю и сигнал с выхода нагрузки не выходит на уставку.
11. Выбрать значения коэффициентов Кр и Кд из области устойчивости в статическом режиме обеспечивают нулевую величину э.д.с. Ер регулируемого источника. По результатам эксперимента рассчитать статизм, перерегулирование и длительность переходного процесса для выбранных значений коэффициентов Кр и Кд. Рассчитать теоретические значения указанных показателей.
Как было видно из п. 10 сигнал ЭДС регулируемого источника не выходит на уставку. В установившемся режиме (p=0) Eр определяется следующим образом:
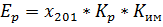
Из выражения видно, что для того чтобы в установившемся режиме Eр =0 необходимо, чтобы x 201=0, т.е. сигнал с выхода сумматора:
В установившемся режиме х=100, поэтому необходимо изменить К д:
Проведем моделирование процесса включения при К р=2 К д=1
Из осциллограммы видно, в установившемся режиме Eр =0 и х=100
Для разделения схемы на сильноточную и слаботочную необходимо задать Кд=0,1.
Произведем моделирование процесса при Кд=0,1 и К р=2
В установившемся режиме Ер не равен 0 и сигнал с выхода нагрузки не равен 100. Необходимо обеспечить: 
Но при таких данных это не выполняется, т.к.:
Поэтому введем в схему пропорциональное звено с передаточной функцией:
|
|
|
Подберем значение коэффициента Кпр:
Модель в программе РИТМ:
BLT103 – генератор кусочно-постоянного сигнала
BLT135 – сумматор
BLT133 – инерционное звено I-ого порядка
BLT089 – пропорциональное звено
BLT014 – осциллограф
BLT015 – табулятор
Выполним моделирование процесса включения:
Теперь в установившемся режиме Ep=0 и х =100.
Для расчета статизма необходимо воздействие выполним моделирование при ЭДС основного источника равном 300.
Рассчитаем статизм перерегулирование и длительность переходного процесса.
Статизм:
Перерегулирование:
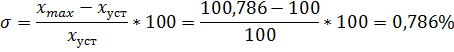
Длительность переходного процесса:
Рассчитаем эти же параметры теоретически
Передаточная функция:
Характеристический полином:
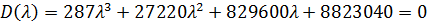
Корни характеристического полинома:
λ1 =-47.885282
λ2 =-23.478962+9.525612i
λ3 =-23.478962-9.525612i
Показатель колебательности:
Перерегулирование:
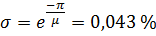
Статизм:
Передаточная функция имеет следующий вид:
В установившемся режиме р =0 и статизм определится следующим образом:
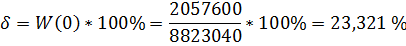
Длительность переходного процесса:
Сравним теоретические и экспериментальные результаты:
| Определение |  , %
|  , %
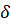| T, c |
| Теоретическое | 0,786 | 23,321 | 0,127 |
| Экспериментальное | 0,043 | 23,32 | 0,100 |
| Погрешность, % | 94,5 | 0,004 | 21,3 |
Расчет погрешности:
12. Подготовить имитационную модель, позволяющую за один расчет выполнить:
моделирование процесса включения системы питания при нулевых начальных условиях с получением установившегося режима;
моделирование последующего переходного процесса, обусловленного потерей 50% величины э.д.с. Е0 с получением нового установившегося режима.
По результатам эксперимента определить статизм, перерегулирование и длительность протекания процесса. Сравнить с результатами выполнения п. 11.
Будем использовать ту же модель что и в п.11. Изменим только величину ЭДС E0 при аварии в блоке 7 BLT103. Вместо 300 установим 50% от нормальной величины, 194,4.
Рассчитаем статизм, перерегулирование и длительность переходного процесса.
Статизм:
Перерегулирование:
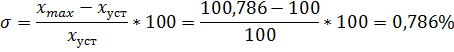
Длительность переходного процесса:
Рассчитаем эти же параметры теоретически
Передаточная функция:
Характеристический полином:
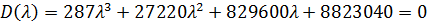
Корни характеристического полинома:
|
|
|
λ1 =-47.885282
λ2 =-23.478962+9.525612i
λ3 =-23.478962-9.525612i
Показатель колебательности:
Перерегулирование:
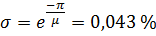
Статизм:
Передаточная функция имеет следующий вид:
В установившемся режиме р =0 и статизм определится следующим образом:
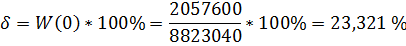
Длительность переходного процесса:
Сравним теоретические и экспериментальные результаты:
| Определение | , %
| , %
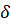| T, c |
| Теоретическое | 0,786 | 23,321 | 0,127 |
| Экспериментальное | 0,043 | 23,317 | 0,100 |
| Погрешность, % | 94,5 | 0,02 | 21,3 |
Расчет погрешности:
Результаты расчетов в п.11 и п.12 совпадают, т.к. система линейна и поэтому статизм, перерегулирование и длительность переходного процесса не будут зависеть от величины возмущения.
13. Провести поэтапную оптимизацию коэффициентов Kp и Kд с целью обеспечения допустимых значений показателей качества, заданных преподавателем
Необходимо обеспечить следующие показатели качества:
δ=5% σ=15%
Так как в установившемся режиме Eрег=0, то изменять K д мы не можем. Следовательно, будем изменять K р. Зафиксируем K д=0,1. Рассчитаем теоретически статизм и перерегулирование.
Характеристический полином:
Корни:
Показатель колебательности:
Перерегулирование:
Статизм:
Передаточная функция имеет следующий вид:
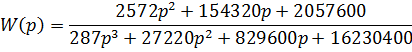
В установившемся режиме р =0 и статизм определится следующим образом:
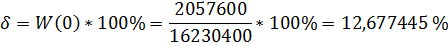
Время переходного процесса:
Экспериментально определим статизм и перерегулирование при K p=20, K д=0,1:
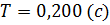
| Определение | , %
| , %
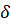| T, c |
| Теоретическое | 14,2 | 12,677 | 0,190 |
| Экспериментальное | 12,3 | 12,677 | 0,200 |
| Погрешность, % | 13,4 | 5,3 |
Расчет погрешности:
Аналогично найдем статизм и перерегулирование при K p=82 и K д=0,1 и получим:
Характеристический полином:
Корни:
Показатель колебательности:
Перерегулирование:
Статизм:
Передаточная функция имеет следующий вид:
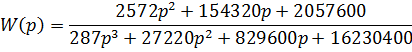
В установившемся режиме р =0 и статизм определится следующим образом:
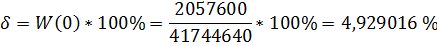
Время переходного процесса:
Экспериментально определим статизм и перерегулирование при K p=82, K д=0,1:
| Определение | , %
| , %
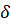| T, c |
| Теоретическое | 60,067 | 4,929 | 0,442 |
| Экспериментальное | 40,279 | 4,929 | 0,48 |
| Погрешность, % | 32,9 | 8,6 |
|
|
|
Расчет погрешности:
Из результатов теоретического расчета видно что при увеличении K p возрастает показатель колебательности и следовательно перерегулирование 
(на границе области устойчивости K p=171 и K д=0,1 показатель колебательности
), но уменьшается статизм 
– гиперболическая зависимость. Следовательно, в данной системе, изменяя K p, невозможно достичь данных показателей качества.
Для обеспечения необходимых показателей качества реализуем астатическое управление, которое должно обеспечить нулевой статизм. Для реализации астатического управления нужно чтобы на предпоследнем этапе эквивалентирования интегрирующее звено попало в глобальную обратную связь. Исходная схема САУ имеет вид:
Перенос сумматора:
Добавим интегрирующее звено в глобальную обратную связь:
В схеме есть несколько мест, в которые поставив интегрирующее звено, оно попадет в глобальную обратную связью:
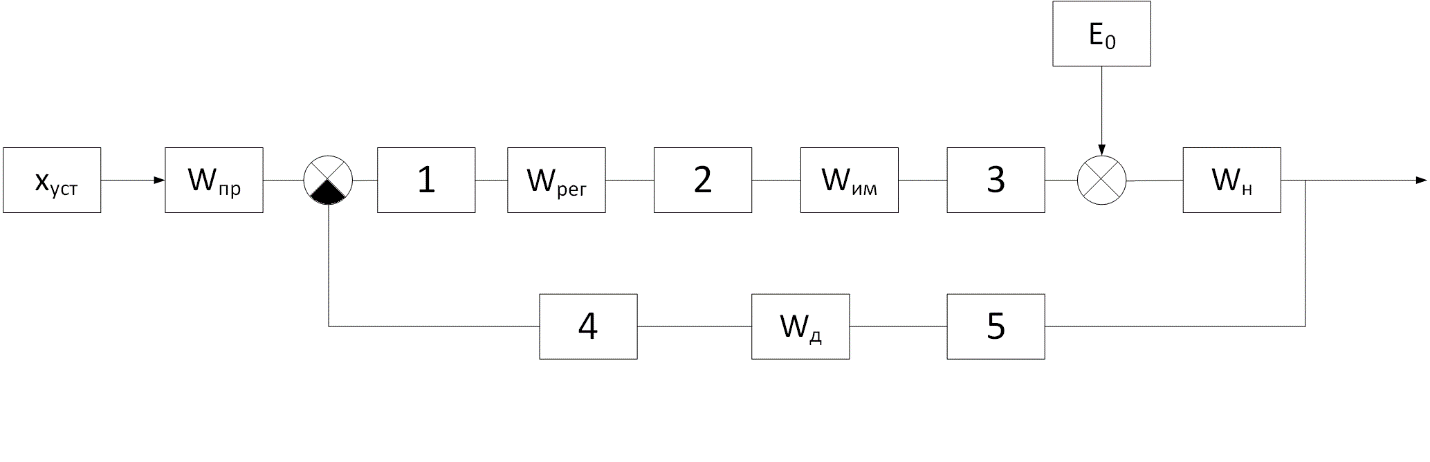
Не во все места можно поставить интегрирующее звено. В 3 и 5 нельзя т.к. это сильноточная часть схема и поэтому в техническом плане схема будет дорога. При установке в 4 или 5 место в установившемся режиме сигнал с выхода регулятора не будет равен 0.
Поэтому можно поставить интегрирующее звено в 1 или 2 место. Эта часть схемы слаботочная. Поставим интегрирующее звено в 1 место и найдем эквивалентную передаточную функцию и область устойчивости. Имеем следующую схему:
Эквивалентная передаточная функция:
Характеристический полином:
Границы устойчивости:
Матрица Гурвица:
Предпоследний минор матрицы Гурвица:
Границы области устойчивости найдем из причин нарушения устойчивости:
1) Появление нулевого вещественного корня: 
2) Равенство нулю предпоследнего минора матрицы Гурвица:
Границы области устойчивости определятся следующими уравнениями:
1) 
3) 
Область устойчивости:
Проверка областей:
Область устойчивости составляют 2 и 5 области.
Проведем моделирование. Коэффициенты установим следующие K p=0,5 K д=0,1 K инт=150. K p берем такой величины чтобы обеспечить запас по перерегулированию (K инт может изменяться в пределах 0 – 1064,5, из области устойчивости).
Модель в программе РИТМ:
BLT103 – генератор кусочно-постоянного сигнала
BLT135 – сумматор
BLT133 – инерционное звено I-ого порядка
BLT089 – пропорциональное звено
BLT014 – осциллограф
BLT015 – табулятор
BLT132 – интегрирующее звено
Экспериментальный расчет:
Теоретический расчет:
Характеристический полином:
|
|
|
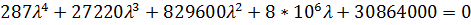
Корни:
Показатель колебательности:
Перерегулирование:
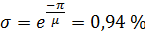
Статизм:
Передаточная функция имеет следующий вид:
В установившемся режиме р =0 и статизм определится следующим образом:
Время переходного процесса:
Сравнение результатов
| Определение | , %
| , %
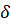| T, c |
| Теоретическое | 0,94 | 0,464 | |
| Экспериментальное | 8,658 | 0,560 | |
| Погрешность, % | 20,7 |
Расчет погрешности:
Из результатов видно, что астатическое управление обеспечило нулевой статизм, но увеличилась длительность переходных процессов.
Выполним моделирование при других значениях коэффициента Кинт.
При Кинт =450, K p=0,5 K д=0,1
При Кинт =50, K p=0,5 K д=0,1
Как видим из осциллограмм при Кинт >150 увеличивается перерегулирование, длительность переходных процессов и возникает различие в длительности протекания переходных процессов.
При Кинт <150 перерегулирование уменьшается, но длительность переходных процессов неодинакова.
Поэтому был выбран Кинт =150, при таком коэффициенте обеспечивается одинаковая длительность протекания переходных процессов и запас по перерегулированию
Предложить и реализовать схемные мероприятия, направленные на повышение точности системы в статических режимах и обеспечение требуемых показателей качества переходных процессов в соответствие с заданием преподавателя.
Необходимо увеличить быстродействие системы в два раза. Имеем следующую длительность переходного процесса:
T эксп=0,560 (с) Т расч=0,464 (с)
Чтобы увеличить быстродействие системы, необходимо скомпенсировать самую медленную постоянную времени системы. В нашем случае это постоянная времени исполнительного механизма Тим=0,05 (с). Т.к. мы вводили интегрирующее звено, то самый простой способ улучшения быстродействия - это ввести ему параллельно пропорциональное звено и таким образом получить корректирующее пропорционально-интегрирующее звено.
Подберем постоянную времени пропорционального звена так, чтобы скомпенсировать постоянную времени интегрирующего звена.
Модель в программе РИТМ:
BLT103 – генератор кусочно-постоянного сигнала
BLT135 – сумматор
BLT133 – инерционное звено I-ого порядка
BLT089 – пропорциональное звено
BLT014 – осциллограф
BLT015 – табулятор
BLT132 – интегрирующее звено
Проведем эксперимент и расчет.
Статизм:
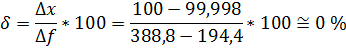
Перерегулирование:
Длительность переходного процесса:
T =0,560 (c)
Теоретическое определение.
Эквивалентная передаточная функция:
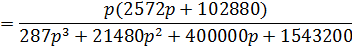
Характеристический полином:
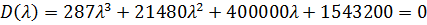Корни:
λ1=-5,218362
λ2=-21,340075
λ3=-48,284769
Статизм:
Показатель колебательности:
Перерегулирование:
Длительность переходного процесса:
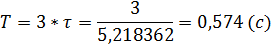
Как видим из результатов введение корректирующего пропорционально-интегрирующего звена привело к появлению еще большей постоянной времени. Изменение настроек системы привело к изменению коэффициентов характеристического полинома. Из-за изменения коэффициентов полинома изменили положение корни.
Сравнение результатов:
| Определение | , %
| , %
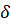| T, c |
| Теоретическое | 0,574 | ||
| Экспериментальное | 8,328 | 0,560 | |
| Погрешность, % | - | 2,44 |
Расчет погрешности:
Так как имеется запас по перерегулированию, увеличим коэффициенты Кинт и Кпр2 так чтобы их отношение не изменилось. Установим Кинт=300 и Кпр2=15 проведем моделирование и расчет:
Статизм:
Перерегулирование:
Длительность переходного процесса:
T =0,320 (c)
Теоретическое определение.
Эквивалентная передаточная функция:
Характеристический полином:
Корни:
λ1=-52,027934
λ2=-11,407636+j8,750008
λ3=-11,407636- j8,750008
Статизм:
Показатель колебательности:
Перерегулирование:
Длительность переходного процесса:
Сравнение результатов
| Определение | , %
| , %
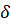| T, c |
| Теоретическое | 1,664 | 0,263 | |
| Экспериментальное | 14,6 | 0,320 | |
| Погрешность, % | 21,7 |
Расчет погрешности:
| Т,с | Ттеор | Тэксп |
| до ускорения | 0,464 | 0,560 |
| после ускорения | 0,236 | 0,320 |
Даже имея запас по перерегулированию не удается ускорить систему с помощью пропорционально-интегрирующего звена. В системе имеются после компенсации самой большой постоянной времени, постоянной времени исполнительного механизма Тим=0,05 с, остается две близких постоянных времени: постоянная времени нагрузки Т=0,0287 с и постоянная времени регулятора Тр=0,025 с. Такая близость приводит к тому, что возникает такая составляющая движения у которой постоянная времени больше постоянных времени регулятора и исполнительного механизма. Из-за этого ускорение системы затруднено. Поэтому была изменена постоянная времени нагрузки.
Передаточная функция нагрузки имеет вид:
Постоянная времени нагрузки:
Уменьшив L мы уменьшим и постоянную времени, при этом коэффициент передачи не изменится. Необходимо уменьшить постоянную времени нагрузки до T* =0,015 (с). Исходное значение L=0,09 Гн. Новое значение L определится как:
Выполним моделирование включение системы без ускорения и с ускорением при новом значении постоянной времени нагрузки. Значения коэффициентов передачи K p=0,5 K д=0,1, Кинт= 150
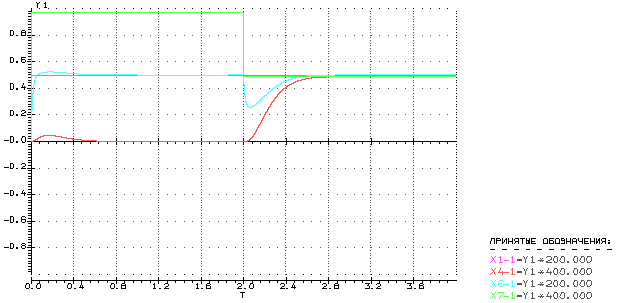
Из осциллограммы видно, что не обеспечивается одинаковая длительность переходных процессов. Установим Кинт= 200и снова проведем моделирование.
Видим, что длительность переходных процессов одинаковая.
Рассчитаем статизм, перерегулирование и длительность переходного процесса:
Экспериментально:
Теоретический расчет:
Характеристический полином:
Корни:
Показатель колебательности:
Перерегулирование:
Статизм:
Передаточная функция имеет следующий вид:
В установившемся режиме р =0 и статизм определится следующим образом:
Время переходного процесса:
Сравнение результатов
| Определение | , %
| , %
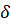| T, c |
| Теоретическое | 3,17 | 0,435 | |
| Экспериментальное | 5,95 | 0,420 | |
| Погрешность, % | - | 3,4 |
Расчет погрешности:
Выполним ускорение системы. Модель используем ту же, что и ранее. Кинт=200, K p=0,5 K д=0,1. Коэффициент передачи пропорционального звена:
Рассчитаем статизм, перерегулирование и длительность переходного процесса:
Экспериментально:
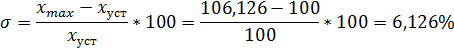
Теоретический расчет:
Характеристический полином:
Корни:
Показатель колебательности:
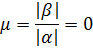
Перерегулирование:
Статизм:
Передаточная функция имеет следующий вид:
В установившемся режиме р =0 и статизм определится следующим образом:
Время переходного процесса:
Сравнение результатов
| Определение | , %
| , %
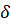| T, c | ||
| Теоретическое | 0,432 | ||||
| Экспериментальное | 6,126 | 0,400 | |||
| Погрешность, % | - | 7,4 | |||
| Расчет погрешности: | |||||
|
| 
| ||||
| Т,с | Ттеор | Тэксп |
| до ускорения | 0,435 | 0,420 |
| после ускорения | 0,432 | 0,400 |
Система ускорилась совсем незначительно. Установим Кинт=500, т.к. имеется запас по перерегулированию и снова проведем моделирование. Коэффициент передачи пропорционального звена:
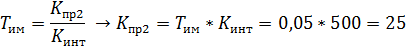
Рассчитаем статизм, перерегулирование и длительность переходного процесса:
Экспериментально:
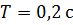
Теоретический расчет:
Характеристический полином:
Корни:
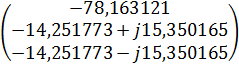
Показатель колебательности:
Перерегулирование:
Статизм:
Передаточная функция имеет следующий вид:
В установившемся режиме р =0 и статизм определится следующим образом:
Время переходного процесса:
Сравнение результатов
| Определение | , %
| , %
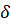| T, c |
| Теоретическое | 5,41 | 0,211 | |
| Экспериментальное | 13,034 | 0,2 | |
| Погрешность, % | 5,2 |
Расчет погрешности:
В итоге имеем:
| Т,с | Ттеор | Тэксп |
| до ускорения | 0,435 | 0,420 |
| после ускорения | 0,211 | 0,200 |
Следовательно, система ускорилась в два раза.
Максимальное значение E=E0+Ep=388,8+54,6=443,4 (В)
Не превышает двойную величину E0=777,6 (В), поэтому изоляция выдержит превышение напряжения.
15. Выводы:
В данной работе было произведено исследование системы электропитания с регулируемым источником, а также выполнена ее поэтапная оптимизация с целью повышения качества регулирования и улучшения переходных процессов и стационарных режимов.
В первой части работы была исследована нагрузка. Двумя способами получено описание звена нагрузки: в виде сокращенной записи дифференциального уравнения и в виде передаточной функции. Результаты совпадают, что говорит о правильно проведенных расчетов. Также были построены экспериментально и теоретически переходная характеристика и амплитудно-фазовая частотная характеристика звена нагрузки. Данные характеристики позволяют анализировать изменение выходного сигнала звена в зависимости от входного.
Во второй части работы было проведено исследование и поэтапная оптимизация системы автоматического управления. По найденному характеристическому полиному была определена область устойчивости системы. Путем установки коэффициента передачи датчика КД =0,1 система была разделена на сильноточную и слаботочную. К системе предъявлялись следующие требования: статизм 5%, перерегулирование 15%. На характеристики системы мы могли воздействовать только путем изменения коэффициента передачи регулятора, т.к. изменение КД приводило к неравенству нулю ЭДС регулируемого источника в нормальном установившемся режиме. Было доказано, что изме
|
|
|
