Билет 13 MathCAD. Основные возможности. Принципы работы.

Mathcad — программа для выполнения и документирования инженерных и научных расчётов.Рабочая область программы представляется как обыкновенный лист, на котором уравнения и выражения отображаются графически, а не в текстовом виде.

Основные возможности Mathcad:Решение дифференциальных уравнений различными численными методамиПостроение двух- и трёхмерных графиков функцийИспользование греческого алфавита как в уравнениях, так и в текстеВыполнение вычислений в символьном режимеВыполнение операций с векторами и матрицамиСимвольное решение систем уравненийАппроксимация

кривыхВыполнение подпрограммПоиск корней многочленов и функцийПоиск собственных чисел и векторовВычисления с единицами измерения

Несмотря на то, что данная программа ориентирована на пользователей, мало знакомых с программированием, она всё же находит применение в достаточно сложных проектах для визуализации результатов математического моделирования с использованием распределённых вычислений и традиционных языков программирования. Также Mathcad часто используется в крупных инженерных проектах, где большое значение имеет трассируемость и соответствие стандартам.

Mathcad - программное средство, среда для выполнения на компьютере разнообразных математических и технических расчетов, снабженная простым в освоении и в работе графическим интерфейсом, которая предоставляет пользователю инструменты для работы с формулами, числами, графиками и текстами. В среде Mathcad доступны более сотни операторов и логических функций, предназначенных для численного и символьного решения математических

Прямые методы решения СЛАУ

Прямые (или точные) методы, позволяют найти решение за определённое количество шагов. Итерационные методы, основаны на использовании повторяющегося процесса и позволяют получить решение в результате последовательных приближений.

1. Формальное решение строится по формулам Крамера

2. Метод Гаусса (приведение матрицы к треугольному виду и послед. Нахождения корней) a. Прямой метод b.обратный метод(Жордана - Гаусса)

3. LU разложение это Ax=LUx=f, где U-треугольная матрица приведенная по методу Гаусса. Ux=y, где y это столбец свободных коэфицентов полученный из f методом Гаусса (; )

4. Метод квадратного корня (метод Холецкого)

5. Метод с ленточной матрицей (метод прогонки)

6. Сокращённый метод Гаусса

7. Метод Холецкого для симметр. Матриц

 

Итерационные методы решения СЛАУ.

1. Метод Гаусса-Зейделя

2. Метод релаксации (обобщение м. Зейделя)

3. Метод уточнения решения полученного прямым методом

4. Метод плоских вращения (Якоби)

5. Циклический метод Якоби с барьерами (более эффективен в случаях большой размерности)

6. Метод Гивенса

7. Метод обратных итераций

8. Другие двухслойные методы (м. минимальных невязок и поправок, м. скорейшего спуска, м. сопряженных градиентов…)

Каноническая форма итерационных методов.

Канонический вид одношаговых итерационных методов для решения системы линейных алгебраических уравнений Ax = f

где В_к+1 - квадратная матрица n n,  _k+1 > 0 - итерационный параметр. В дальнейшем будем использовать следующие согласованные нормы в конечномерном пространстве размерности n:

Итерационный метод сходится, если .

Опр. Величина z_k = x_k - x называется погрешностью решения.

Опр. Если B_k+1 = B и  _k+1 =  то метод называется стационарным

Метод Зейделя

Метод релаксации

Метод простой итерации

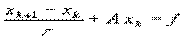
Метод Якоби

⇐ Предыдущая123Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: