Моделирование поверхностей в проекциях с числовыми отметками

Поверхности в проекциях с числовыми отметками задаются линиями уровня (горизонталями), являющимися линиями пересечения заданной поверхности с горизонтальными плоскостями. Земную поверхность принято называть топографической поверхностью. Топографическая поверхность изображается горизонталями, плавными линиями, соединяющими точки поверхности с одинаковыми отметками. Разность отметок между горизонталями выбирается в зависимости от рельефа местности и масштаба. Линия пересечения топографической поверхности с вертикальной плоскостью называется профилем. Линия ската применительно к поверх­ностям обычно рассматривается для конкретной точки и проводится пер­пендикулярно горизонталям, проходящим через нее.

Задача градуировки является часто встречающейся задачей, решае­мой применительно к поверхностям в проекциях с числовыми отметками. Рассмотрим решения этой задачи для некоторых поверхностей.

А). Коническая поверхность

Коническая поверхность может быть представлена как прямым конусом с вертикальной осью, так и наклонным конусом, рассмотрим вначале прямой конус. Сечения конической поверхности горизонтальными плоскостями дадут ряд окружностей. В случае прямого конуса, проецируя их на горизонтальную плоскость, получаем ряд концентрических окруж­ностей (рис. 5.5). Линию наибольшего ската для прямого конуса можно получить, проградуировав образующую конуса. Такая градуировка позво­ляет провести и соответствующие горизонтали прямого конуса. Для выполнения этой операции, необходимо знать отметки каких либо двух точек на образующей или отметку одной точки и уклон.

Б). Цилиндрическая поверхность

Если образующие цилиндра вертикальны, то горизонтальная проекция ци­линдра представляет собой окружность, т.е. является вырожденной. В этом случае в проекциях с числовыми отметками указывают на вырожденной проекции отметку верха цилиндра. Особого интереса этот случай не представляет. Если ось цилиндра горизонтальна, то задача градуирова­ния поверхности сводится к отысканию образующих, отметки которых выра­жены целыми числами. Для этого строим вертикальную проекцию цилиндра или той его части, которую необходимо проградуировать (рис. 5.6). Проградуировав ее по высоте, проведем вертикальные проекции горизонталь­ных плоскостей. Отметим точки их пересечения с вертикальной проекцией цилиндра и перенесем на проекцию с числовыми отметками проекции иско­мых образующих. Линия ската для любой точки такой поверхности предс­тавляет из себя дугу окружности.

 

 

 

Рис. 5.5.Коническая поверхность

 

 

Рис. 5.6.Цилиндрическая поверхность

 

 

В). Сферическая поверхность

Градуирование сферической поверхности производится по тому же принци­пу, что и градуирование поверхности цилиндрической (рис. 5.7). Строится вертикальная проекция сферы, градуируется ее вертикальная ось, нахо­дятся точки пересечения вертикальных проекций горизонтальных плоскостей с вертикальной проекцией сферы. Затем на фронтальной проекции сферы отмечают радиусы окружностей, которые отсекают горизонтальные плоскости на поверхности сферы. Этими радиусами проводят искомые ок­ружности – горизонтали на проекции с числовыми отметками. Линия ската для любой точки сферической поверхности также представляет из себя дугу окружности.

 

 

Рис. 5.7.Сферическая поверхность

 

Г). Поверхность равного уклона

Если прямой круговой конус за вершину перемещать по какой-либо кривой (рис. 5.8), то полученная при этом перемещении поверхность образует поверхность равного уклона. Конус является определителем этой поверх­ности, а кривая – направляющей. Для любой точки такой поверхности ли­ния ската имеет одинаковый наклон к горизонтальной плоскости проек­ции. При градуировании такой поверхности нужно иметь в виду, что ук­лон поверхности в любой ее точке одинаков и расстояние между смежными горизонталями равно интервалу линии ската. Для градуирования размеща­ем конусы в точках заданной определяющей кривой и градуируем их по­верхности. На практике (рис. 5.9) это выглядит как проведение из точек кривой концентрических окружностей, радиусы которых отличаются на ве­личину интервала, а высотные отметки на единицу. Проведя кривые линии, соприкасающееся с этими горизонталями конических поверхностей, имеющих одну и ту же отметку, получим горизонтали поверхности равного уклона.

 

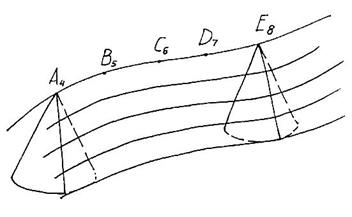
Рис. 5.8.Поверхность равного уклона

 

Рис. 5.9. Построение поверхности равного уклона

 

Д). Топографическая поверхность

Земная (топографическая) поверхность представляется горизонталь­ной проекцией каркасной модели образующейся при рассечении земной по­верхности горизонтальными плоскостями. По возрастанию горизонталей можно судить о виде изображенной поверхности. Так, на рис. 5.10, а) изоб­ражено повышение местности (холм), а на рис. 5.10, б) ее понижение. В до­полнение к высотным отметкам на горизонталях обычно проставляются Берг штрихи показывающие направление понижения местности. Важным допу­щением в проекциях с числовыми отметками является допущение о линей­ном характере изменения местности между ее горизонталями.

Это предпо­ложение позволяет решать следующие задачи:

1. Находить отметки промежуточных точек местности (рис. 5.10, б). Например, для определения отметки точки А, проведем через нее от­резок произвольного направления. Начало (точка В) и конец (точка С) отрезка находятся на соседних с точкой А горизонталях. Проведя операцию соот­ветствующую градуировке отрезка, определим отметку точки А – 15.8.

а) б)

Рис. 5.10.Топографическая поверхность

2. Производить построение линии ската поверхности (рис. 5.11). Например, направление линии наибольшего ската в точке D будет совпадать с направлением перпендикуляра проведенного из этой точки к соседней горизонтали в направлении убывания отметок (показано стрелкой). Определение самой линии наибольшего ската для произвольной точ­ки поверхности (например, точка А) производится следующим образом: Опускаем перпендикуляр на соседнюю горизонталь (точка С). Так как поверхность криволинейна то перпендикуляр восстановленный из точки С в обратном направлении с исходной точкой А не совпадет, а окажется в точке Е. Биссектриса угла АСЕ даст направление линии наибольшего ска­та в ближайших к исходной точке А точках поверхности. Для точки А ли­нию наибольшего ската проведем параллельно биссектрисе угла АСЕ. Су­ществуют и более точные способы построения линии наибольшего ската.

3. Определять линию сечения топографической поверхности проецирующей плоскостью. Такое сечение (рис.5.12, а) и б) называется профилем поверхности. Секущая плоскость задана своей горизонтальной проекцией γ. Отметив точки пересечения плоскости с горизонталями поверхности пост­роим профиль поверхности. Для этого выберем базовую горизонталь соот­ветствующую, или несколько ниже, минимальной отметки горизонтали местности пересекаемой плоскостью v. Проведя перпендикулярно следу плоскости линии связи, отложим на них отметки соответствующих гори­зонталей и соединим их плавной кривой. Обычно масштаб, в котором отк­ладываются вертикальные отметки по линиям связи, больше горизонталь­ного масштаба. В этом случае получаемый профиль более выразителен. На профиль наносится сетка горизонталей. Первая горизонталь профиля на­зывается базовой. Профиль может быть наложенным, как показано на рис. 5.12, а), так и вынесенным (рис.5.12, б). В случае вынесенного профиля базовая горизонталь может располагаться в произвольном месте чертежа с произ­вольной ориентацией относительно следа секущей плоскости (см. образец выполнения графического задания).

4. Находить пересечение прямой линии с топографической поверх­ностью (рис.5.13). Данная задача разбивается на следующие этапы:

а) градуируем заданную прямую АВ,

б) заключаем прямую в плоскость общего положения α, уклон которой соответствует уклону прямой,

в) находим точки пересечения горизонталей данной плоскости с со­ответствующими горизонталями топографической поверхности (поскольку плоскость, в которую заключаем прямую, имеет произвольную ориентацию, то горизонтали этой плоскости, оставаясь параллельны между собой, к прямой линии АВ наклонены под произвольным углом),

г) соединив полученные точки плавной кривой, получим линию пересечения плоскости ее и топографической поверхности. В точке пересечения данной линии и заданной прямой линии находится искомая точка К пересе­чения топографической поверхности и прямой АВ.

 

 

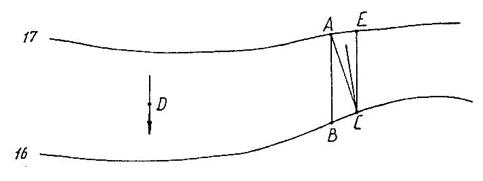
Рис. 5.11.Построение линии ската поверхности

 

 

Рис. 5.12.Сечение топографической поверхности

 

Рис. 5.13..Пересечение прямой линии с поверх­ностью

 

⇐ Предыдущая123Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: