Кавитационные режимы движения жидкости

В жидкости при любом давлении и температуре всегда растворено какое-либо количество газов. Уменьшение давления в жидкости ниже давления насыщения жидко­сти газом сопровождается выделением рас­ творённых газов в свободное состояние, и, ГпасЬики Г.А. Муоина наоборот, при повышении давления, выде-

лившиеся из жидкости газы, вновь переходят в растворённое состояние. Изменение дав­ления в жидкости может приводить и к изменению агрегатного состояния жидкости (пе­реход жидкости в пар и пара в жидкое состояние). Если жидкость движется в закрытой системе, то колебания давления в потоке могут приводить к образованию локальных зон низкого давления и как следствие, в этих зонах происходят процессы образования паров жидкости («холодное» кипение жидкости) и её раз газирование. При этом, процесс разга-зирования, как правило - процесс более медленный, чем процесс парообразования. Одна­ко и в том и в другом случае появление свободного газа и, тем более пара, в замкнутом пространстве крайне не желательно. Появление пузырьков газовой фазы говорит о том, что в жидкости появился разрыв. Далее эти пузырьки переносятся движущейся жидко­стью. Процесс образования пузырьков пара в жидкости носит название паровой кавита­ции, образование пузырьков газа вызывает газовую кавитацию. При попадании в зону вы­сокого давления пузырьки газа растворяются в жидкости, а пузырьки пара конденсируют-

ся. Поскольку последний процесс происходит почти мгновенно, говорят о том, что пу­зырьки схлопываются. Особенно интенсивно процессы схлопывания пузырьков пара про­исходит в месте контакта их с твёрдыми телами (стенки труб, элементы гидромашин и т.д.). Отрицательное воздействие пузырьков пара на элементы гидросистем заключаются в особенности их контакта с твёрдыми телами: при приближении к твёрдой границе пу­зырьки пара деформируются, что приводит к явлению подобному детонации. При таком воздействии свободного пара и газа на твердые элементы внутренних конструкций гидро­машин, они разрушаются и выходят из строя. Для оценки режима течения жидкости вво­дят специальный критерий; число кавитации К ^f '

7. Истечение жидкости из отверстий и насадков >

Отверстие в тонкой стенке

Одной из типичных задач гидравлики, которую можно назвать задачей прикладного

характера, является изучение процессов, связанных с истечением жидкости из отверстия в тонкой стенке и через насадки. При таком движении вся потенциальная энергия жидкости находящейся в ёмкости (резервуаре) в конечном итоге расходуется на кинетическую энер­гию струи, вытекающей в газообразную среду, находящуюся под атмосферным давлением или (в отдельных случаях) в жидкую среду при определённом давлении. Отверстие будет считаться малым, если его размеры несоизмеримо малы по сравнению с размером свобод­ной поверхности в резервуаре и величиной напора. Стенка называется тонкой, если вели­чиной гидравлических сопротивлений по длине канала в тонкой стенке можно пренеб­речь. В таком случае частицы жидкости со всех сторон по криволинейным траекториям движутся с некоторым ускорением к отверстию. Дойдя до отверстия, струя жидкости от­рывается от стенки и испытывает преобразования уже за пределами отверстия.

Истечение жидкости из отверстия в тонкой стенке при установившемся

Движении (жидкости).

Истечение жидкости в газовую среду при атмосферном давлении. При истечении из

отверстия в тонкой стенке криволи­нейные траектории частиц жидкости сохраняют свою форму и за пределами отверстия, т.е. после выхода из отвер­стия сечение струи уменьшается и дос­тигает минимальных значений на рас­стоянии равном (d - диаметр отверстия). Таким образом, в сечении В - В будет находиться как назы­ваемое сжатое сечение струи жидкости. Отношение площади

чения струи к площади отверстия называется коэффсщииитоживинфиясфэ&мзвтачаетр^ивсек

гда:

где: s - площадь отверстия,

з_сж - площадь сжатого сечения струи, s - коэффициент сжатия струи.

Запишем уравнение Бернулли для двух сечений А -А и В -В. В связи с тем, что от­верстия в стенке является малым сечение В -В можно считать «горизонтальным» (ввиду малости отверстия), проходящим через центр тяжести сжатого сечения струи.

i. *"*

Поскольку величина скоростного напора на свободной поверхности жидкости (сече­ние А - А) мала из-за малости скорости, то её величиной можно пренебречь. В данном случае истечение жидкости происходит в атмосферу, следовательно р_{ - р₀. Тогда:

^т г

F> f

Поскольку в тонкой стенке потери напора по длине бесконечно малы, то

где' 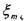- коэффициент потерь напора в тонкой стенке Следовательно, скорость в сжатом сечении струи будет равна:

Первый сомножитель в равенстве носит название коэффициента скорости'

Определим расход жидкости при её истечении из отверстия (заметим, что скорость истечения жидкости у нас относится к площади сжатого живого сечения струи):

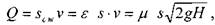
где: - называется коэффициентом расхода.

При изучении процесса истечения жидкости предполага­лось, что ближайшие стенки и дно сосуда находятся на достаточ­но большом удалении от отверстия: , т.е. не ближе тройного расстояния от направляющих стенок. В этом случае все линии тока имеют одинаковую кривизну, и такое сжатие струи

называется совершенным сжатием. В иных случаях близко расположенные стенки явля­ются для струи направляющими элементами, и её сжатие будет несовершенным (не оди-

наковым со всех сторон). В тех случаях, когда отверстие непосредственно примыкает к одной из сторон отверстия (сечение отверстия не круглое), сжатие струи будет неполным. При неполном и несовершенном сжатии струи наблюдается некоторое увеличение коэффициента расхода. При полном совершенном сжатии струи коэффициент сжатия дос­тигает 0,60 - 0,64. Величины коэффициентов сжатия струи, коэффициента расхода зависят

от числа Рейнольдса (см. рисунок), причём коэффициенты сжатия и скорости в разных направлениях: с возрастанием числа Рей­нольдса коэффициент скорости увеличивает­ся, а коэффициент сжатия струи убывает. В результате этого коэффициент расхода оста­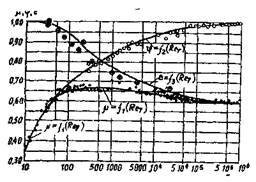 ётся практически неизменным (исключением являются потоки жидкости с весьма малыми числами Рейнольдса).

Величины коэффициента расхода измеряются простым замером фактического расхо­да жидкости через отверстие и сопоставлением его с теоретически вычисленным значени­ем.

Коэффициент сжатия струи измеряется путём непосредственного определения сжа­того сечения струи, коэффициент скорости - по траектории струи.

Истечение жидкости через затопленное отверстие. Истечение через затопленное от­верстие в тонкой стенке, т.е. под уровень жидкости ничем существенным не отличается от истечения в атмосферу.

Пусть в резервуаре имеется перегородка с отверстием, уровни жидкости находятся

на отметках и относи­тельно плоскости сравнения, проходящей через центр тя­жести отверстия. Запишем уравнение Бернулли для свободных поверхностей жидкости (сечение А - А и сечение В - В относительно плоскости сравнения О - О).

Потери напора состоят из двух частей: потеря напора при истечении из отверстия в тонкой стенке (как при истечении в атмосферу):

и потеря на внезапное расширение струи от сжатого сечения до сечения резервуара:

^р *

Подставив полученные выражения для видов потерь в предыдущее уравнение, полу­чим:

В данном случае действующим напором является разность уровней свободных по­верхностей жидкости z. Скорость истечения будет равна:

j * * *

Обозначив: получим выражение для расхода жидкости¹

•>

⇐ Предыдущая78910111213141516Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: