Продольные силы в поперечных сечениях

Под растяжением (сжатием) понимают такой вид нагружения, при котором в поперечных сечениях стержня возникают только продольные силы , а прочие силовые факторы равны нулю.

Рассмотрим однородный прямолинейный стержень длиной и площадью поперечного сечения А, на двух концах которого прило­жены две равные по величине и противоположно направленные центральные продольные силы Р (рис. 2.2, а).

Продольная сила – внутреннее усилие, равное сумме проекций всех внешних сил, взятых с одной стороны от сечения, на ось стержня. Примем следующее правило знаков для продольной силы: растягивающая продольная сила положительна, сжимающая – отрицательна (рис. 2.1).

Рис.2.1

 

Поместим начало плоской системы координат yz в центре тяжести левого сечения, а ось 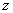направим вдоль продольной оси стержня.

Для определения величин внутренних усилий воспользуемся методом сечений. Задавая некоторое сечение на расстояние z () от начала системы координат и рассматривая равновесие левой относительно заданного сечения части стержня (рис. 2.2, б), приходим к следующему уравнению:

,

откуда следует, что

.

Следовательно, продольная сила в сечении численно равна сумме проекций на ось стержня всех сил, расположенных по одну сторону сечения

(2.1)

Рис. 2.2

 

Для наглядного представления о характере распределения продольных сил по длине стержня строится эпюра продольных сил . Осью абсцисс служит ось стержня. Каждая ордината графика – продольная сила (в масштабе сил) в данном сечении стержня.

Эпюра позволяет определить, в каком сечении действует максимальное внутреннее усилие (например, найти N _max при растяжении-сжатии). Сечение, где действует максимальное усилие будем называть опасным.

Рассмотрим несколько примеров определения внутренних сил.

Пример 1.

Пусть имеется стержень постоянного поперечного сечения, нагруженный силами 2 Р и 3 Р вдоль продольной оси стержня, показанный на рис.2.3. Определить величину внутренних сил.

Рис.2.3

 

Решение.

Стержень может быть разделен на два участка, граничными точками которых являются точки приложения сосредоточенных сил и точка закрепления. Если начало координат расположить на правом конце стержня, а ось z направить справа налево, то, используя метод сечений, рассекая последовательно участки, отбрасывая левую часть, заменяя ее действие внутренними усилиями N, Q_y, M_x и уравновешивая оставшуюся часть, получим:

I участок:

, ;

, ;

,

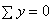Как видно, при растяжении в поперечных сечениях стержня возникает только один внутренний силовой фактор - нормальная сила N.

II участок:

, .

Таким образом, нормальная сила равна алгебраической сумме проекций сил, приложенных к отсеченной части на продольную ось .

Полученные результаты для большей наглядности удобно представить в виде графика, (эпюры N), показывающего изменение продольной силы вдоль оси стержня (рис.2.3). Построим на первом участке линию параллельную оси z на высоте 2 Р, на втором участке – линию со значением - Р. Области ограниченные графиком и осью z принято штриховать и обозначать знак этой области. Видно, что наибольшая продольная сила возникает на первом участке стержня и, как следствие, при прочих равных условиях, он скорее может разрушиться, чем второй участок.

Пример 2.

Построить эпюру продольных сил для жестко защемленной балки (рис.2.4).

Решение:

1. Намечаем характерные сечения, нумеруя их от свободного конца стержня к заделке.

2. Определяем продольную силу в каждом характерном сечении. При этом рассматриваем всегда ту отсеченную часть, в которую не попадает жесткая заделка.

3. По найденным значениям строим эпюру .

Положительные значения откладываются (в выбранном масштабе) над осью эпюры, отрицательные – под осью.

Рис.2.4

 

Пример 3.

Два стержня, соединенные в т. А, находятся под действием силы Р (рис.2.5, а). Определить усилия, действующие в стержнях.

А) б) в)

Рис.2.5

Решение.

Воспользуемся методом сечений. Рассечем стержни в произвольном месте сечения n - n. Отбросим левую отсеченную часть. Заменим отброшенную часть, приложив усилия N₁ и N₂ в сечениях к правой части. Направление усилий целесообразно выбрать так чтобы они растягивали отсеченные части (рис.2.5, б).

Уравновесим отсеченную часть, запишем уравнения ; .

Решая, из первого уравнения получим

,

из второго уравнения окончательно имеем

; .

Так как величина силы N ₂ < 0, то её направление следует изменить на противоположное (рис.2.5, в). Согласно рисунку нормальная сила N ₁ растягивает отсеченную часть стержня 1 - она положительна, сила N₂ сжимает отсеченную часть стержня 2 - она отрицательна.

Пример 4.

Абсолютно жесткий брус подвешен на двух стержнях и находится под действием силы Р (рис.2.6, а). Определить усилия в стержнях.

Решение.

Используя метод сечений, получим отсеченную часть, показанную на рис.2.6, б.

Запишем уравнения равновесия и :

Рис.2.6

 

Решая систему уравнений, получим

; .

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: