 |
Основное уравнение прогнозирования
|
|
|
|
В соответствии с нашей моделью запасы следующего года суть случайные величины, и потому их значения не могут быть предсказаны точно. В этих условиях мы обычно используем ожидаемые величины случайной переменной в качестве прогноза.
Перейдем к математическим ожиданиям в обеих частях уравнения (1) для запасов в год Т. Мы уже отметили, что
,
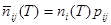где черта над n означает математическое ожидание. Набор в классе j, n0 j (T + 1) можно записать как R (T + 1) rj, так что необходимо найти математическое ожидание для R (T + 1). Имеем 
и из (3) 
,
Теперь, следовательно, с подстановкой в (1) получим
. (4)
Эти уравнения могут быть кратко записаны в матричной форме, например, как
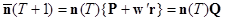. (5)
Таким образом, если параметры модели известны, то запас следующего года (т.е. Т + 1) может быть найден по запасу текущего года (год Т) путем простого перемножения матриц. Прогноз на следующий год, 
, может быть затем использован в качестве основания для прогноза еще на один год вперед, если взять
(6)
(мы не можем писать n (T + 1) в правой части, так как эта величина не известна в год Т; поэтому используем ожидаемую величину).
Матрица Q относится к особому классу матриц, называемых стохастическими, и представляет всевозможные переходы от одного класса к другому. Она имеет неотрицательные элементы, и суммы всех элементов каждой из строк равны единице. Подобные матрицы играют основную роль в теории марковских цепей, и мы можем применить эту теорию для ответа на вопросы о поведении модели.
Прогнозирование
Первый вопрос, который был поставлен относительно структуры преподавательского состава университета, состоял в том, имеется ли тенденция к продолжению роста. На этот вопрос можно ответить, используя запись (6). Допустим, что начальные запасы и величины параметров таковы:
|
|
|
,
где классы перечислены в порядке увеличения уровня квалификации (ассистенты, доценты, профессоры). Вид матрицы Р, представленный выше, вполне типичен. Нули ниже диагонали означают, что движение из более высоких классов в более низкие отсутствует; происходят разве лишь переводы в более высокие классы. Вектор ухода говорит о высоком коэффициенте потерь наверху и внизу; наверху — это смерть и уход в отставку, случающиеся чаще, чем в двух нижних классах. Наибольший уровень приема на работу имеет место в нижнем классе.
Построим матрицу Q и получим структуру классов на 5 и 10 лет вперед с помощью формулы (5). Для этого создаем программу для MatLab uspsvu1.m (текст программы приведен в приложении). Результаты выполнения программы:
— матрица 
;
— структура классов на 5 лет вперед: 
;
— структура классов на 10 лет вперед: 
.
Явно наблюдается постоянно ухудшающееся состояние, поскольку система приобретает признаки перегруженности высоких классов. Такое поведение системы зависит, разумеется, от структуры Р, но был взят весьма типичный случай, который, правда, соответствует большим возможностям для повышения, чем это имеет место во многих организациях. Вывод должен быть таким, что политики набора и повышений, представленные как r и P, несовместимы с сохранением структуры вида n (0). (Необходимо отметить, что элементы вектора предсказанных численностей классов в общем случае не будут целыми; это объясняется тем, что здесь оперируют с математическими ожиданиями. Математику известно, что математические ожидания целых чисел, являющихся случайными переменными, сами не обязательно целые, однако при представлении результатов администрации разговор о дробных значениях числа людей иногда может подорвать доверие к методу!).
|
|
|
Имея прогноз неблагоприятного свойства, необходимо знать меру того, насколько все может стать неблагополучным. В математических терминах — каково предельное состояние n (T) при 
? После Т лет будет
. (7)
В теории марковских цепей показывается при весьма общих условиях, которые будут выполняться в любой разумной постановке задачи о кадрах, что
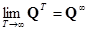, (8)
где Q∞ — стохастическая матрица с одинаковыми строками. Если через q обозначить общую строку этой матрицы, то устремляя Т к бесконечности в (7), получаем
n (∞) = n (0)Q∞ = N q, (9)
где N — общий (фиксированный) размер системы. Следовательно, имеется предельная структура, которая не зависит от начальной структуры. Простейший способ подсчета q связан с тем, что предельная структура должна удовлетворять условию
n (∞) = n (∞)Q или q = qQ. (10)
Эта система уравнений является вырожденной, однако если мы опустим одно из уравнений и используем тот факт, что
,
то уравнения могут быть легко решены. Составляем программу для MatLab uspsvu2.m (текст программы приведен в приложении). Были получены следующие результаты для рассматриваемого примера:
, 
, 
.
Как видно, в конечном итоге ситуация становится очень неблагополучной:
1) превышение численности профессоров над ассистентами;
2) возрастание численности профессоров в 3 раза по сравнению с начальным уровнем при уменьшении численности ассистентов более чем в 2 раза.
В заключении данного параграфа необходимо подчеркнуть 2 момента,
1) в рассматриваемом примере наибольшее ухудшение ситуации происходит в первые 3-5 лет (см. рис. 1), т.е. достаточно быстро.
2) наличие предельной структуры при данных Р, w и r говорит о том, что вполне возможно, изменяя Р, w и r, добиться выполнения условия n = nQ (т.е сохраняемости структуры, начиная с любого года). Об этом подробнее в следующем параграфе.
|
|
|
