 |
Управление: сохраняемость структур
|
|
|
|
С обнаружением неизбежности роста численности более высоких классов с известной скоростью следующей задачей становится задача управления ситуацией. Пусть первой ограниченной целью наших усилий будет удержание системы на том уровне, на котором она находится. Если n — существующая структура, которую хотелось бы сохранить, то она, очевидно, должна удовлетворять условию
n = nQ (11)
В математических терминах задача управления сводится к нахождению матрицы Q, такой, что соотношение (11) удовлетворяется. В то же время Q является некоторой функцией от Р, w и r, а эти величины не все поддаются управлению. Естественные потери, например, не находятся под непосредственным контролем администрации, а увольнение является таким моментом, который большинство работодателей предпочитают избегать. Перевод в более высокий класс находится под непосредственным контролем администрации, однако нехватка подходящих кандидатур на повышение или политика, направленная на заполнение вакансий путем повышений, могут создать для повышений такую ситуацию, когда они будут ограничены тесными рамками. Вектор приема также является объектом непосредственного управления, однако и здесь снова могут возникнуть ограничения из-за возможностей приглашать квалифицированных кандидатов или из-за ограничений, связанных с проводимой политикой.
Математическая задача, с которой мы столкнулись, состоит, таким образом, в поиске матрицы Q, удовлетворяющей условию (11) и учитывающей все те ограничения, которые налагаются практически реализуемой политикой на работу системы. Разумеется, может оказаться вообще невозможным подобрать подходящую политику.
|
|
|
Для иллюстраций решения сделаем довольно простое допущение, которое тем не менее часто соответствует действительности. Допустим, что Р и, стало быть, w вообще не могут быть изменены. Все управление, следовательно, должно быть реализовано через вектор r, который, как мы предполагаем, может изменяться по нашему желанию при условии
. (12)
(Неравенство, связывающее два вектора, должно пониматься как действующее в каждой паре элементов.) В этом случае поставленная задача может быть решена отысканием такого вектора r, который удовлетворяет условиям (11) и (12). Заметив, что 
, легко показать, что
, (13)
где I – единичная матрица; отметим, что nw ’ — скаляр. Можно легко убедиться в том, что элементы вектора r, получаемого по (13), в сумме дают единицу. Вместе с тем эти элементы будут все неотрицательны, если
. (14)
Таким образом можно легко проверить, обладает ли определенная структура способностью сохраняться при управлении наймом.
Такого рода арифметическая проверка годится для достижения непосредственной цели, но она непригодна для того, чтобы прийти к пониманию вопроса о типе структур, которые могут сохраняться. Поэтому мы продолжим поиск характеристик множества структур, которые удовлетворяют условию (14).
Поскольку размеры всей системы фиксированы, будем работать в терминах пропорций каждого из классов и определим их с помощью x = n N -1. Таким образом, будем интересоваться множеством таких х, которые удовлетворяют условию
. (15)
При k = 3 можно сделать задачу геометрически наглядной. Вектор х может быть представлен как точка в трехмерном евклидовом пространстве. Каждая такая точка должна лежать на плоскости x 1 + x 2 + x 3 = 1 и находиться в положительном октанте. Тогда множество всех возможных структур может быть представлено множеством всех точек равностороннего треугольника с вершинами (1, 0, 0), (0,1,0) и (0,0,1), показанного на рис. 2.
|
|
|
Неравенство (15) определяет некоторую область в этом треугольнике, содержащую все структуры, которые могут сохраняться. Если найти границу этой области, то окажется возможным непосредственно увидеть, какого рода структуры сохраняются. Это достигается алгебраическим путем представления всякого х, удовлетворяющего условию (15), в виде линейной комбинации (линейной функции с положительными коэффициентами, дающими в сумме единицу) фиксированного множества вершин. В результате получается, что область сохраняемости является выпуклой оболочкой, определяемой этими вершинами.
Будем рассуждать в терминах произвольного k, однако сохраним геометрическую терминологию, использованную для k = 3.
Из (13) для х получаем
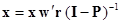. (16)
Умножая обе части соотношения (16) на вектор-столбец из единиц, записываемый как I ’, находим, что
, (17)
где элементы d суть суммы элементов строк матрицы (I – P)-1. Тогда, производя подстановку (17) в (16), получаем
, (18)
где e i — вектор, i -я координата которого 1, а остальные координаты — нули.
Пусть
,
тогда х можно записать как
. (19)
Коэффициенты a i неотрицательны, и их сумма равна единице. следовательно, любая такая точка х лежит в выпуклой области с вершинами, имеющими координаты
,
и каждая такая точка соответствует своему r.
Чтобы проиллюстрировать выкладки, возьмем данные примера из предыдущего параграфа:
.
Для такой матрицы Р получаем
.
Произведя деление каждой строки на сумму элементов этой строки, получаем вершины области, содержащей сохраняющиеся структуры
(0; 0; 1), (0; 0.5; 0.5), (0.429; 0.286; 0.286).
Эти точки нанесены на рис. 2, и область, содержащая сохраняющиеся структуры, есть треугольник. Сделаем проверку. Возьмем, например, структуру (0.429; 0.286; 0.286), домножим ее на общий размер системы N = 450: (193.05; 128.7; 128.7) и подставим в (13), тем самым мы найдем управляемый вектор набора r = (1; 0; 0). Легко проверяется, что структура (193.05; 128.7; 128.7) сохраняется при заданных P, w и найденном r (воспользовавшись, например, программой uspsvu1.m).
|
|
|
Аналогичный анализ можно провести для случая, когда управлять можно только долей повышений. В данном случае мы фиксируем r и w и изучаем влияние изменения элементов Р при ограничении вида di = 1 – wi для всех i. В случае матрицы Р общего вида задача усложняется тем, что имеется бесконечно много матриц Р, удовлетворяющих условию (11). Однако если рассматривается некоторая простая иерархия, в которой повышения проводятся только в следующей, более высокий класс, то Р имеет ненулевые элементы только на главной диагонали и на диагонали над нею. В этом случае существует единственное решение уравнения (11), и множество n, которому соответствует некоторая матрица Р с неотрицательными элементами, представляет область репродуктивности. В отличие от области, определяемой управлением набором, оказывается, что эта область включает структуры с перегруженными более низкими классами. Полученный результат наводит на мысль, что сохраняемость структуры, перегруженной нижними классами, может быть более успешно реализована путем управления повышением, а не набором.
Заключение
Модель системы кадров, которая составила основу данного доклада, разумеется, является слишком упрощенной. Составляющие потерь, например, не могут всегда считаться постоянными в пределах одного класса. Все составляющие обнаруживают склонность к изменениям со временем, и при некоторых условиях достигается возможность планирования этих изменений. Одна из наиболее привлекательных особенностей марковской модели заключается в том, что она может быть легко настроена на охват обобщений такого рода без изменений ее главной структуры. Следовательно, продемонстрированный в этом докладе подход относится к числу подходов, которые остаются пригодными при значительно более общих условиях по сравнению с частными случаями, которые здесь подробно обсуждались.
|
|
|
Выше мы установили различие между использованием модели для прогнозирования и для управления. В первом случае вводимые допущения должны отображать — настолько точно, насколько это возможно, — реальное поведение системы в недавнем прошлом. При использовании модели для управления допущения распадаются на две группы. Те допущения, которые относятся к неуправляемым аспектам системы, должны, как и в случае прогнозирования, отражать действительность. Те же, которые относятся к переменным управления, имеют другой характер: они касаются возможностей администрации и, таким образом, должны основываться на сведениях об организации системы.
Приложение
1) Текст программы uspsvu1.m:
% uspsvu1.m - программа прогнозирования структуры преподавательского
% состава на любое количество лет
% Автор: студент ДГТУ группы У-3-47 В.В.Груздев < 21.05.02 >
clc;clear;
disp('Вектор запасов на текущий год');
n=[300 100 50]
disp('Вектор вероятнотей ухода (увольнение или что-либо еще)');
w=[0.2 0.1 0.2]
disp('Вектор, определяющий распределение нанимаемых по классам');
r=[0.75 0.25 0]
disp('Матрица вероятностей переходов, управляющая перемещениями в системе')
P=[0.6 0.2 0;
0 0.7 0.2;
0 0 0.8]
% Вероятностная матрица (матрица Маркова)
Q=P+w'*r;
while 1==1
t=input('Enter year: ');
if t<1 break; end
Qt=Q^t;
disp(sprintf('Вектор запасов на %d лет вперед:',t));
nt=n*Qt
end
2) Текст программы uspsvu2.m:
% uspsvu2.m - программа прогнозирования структуры преподавательского
% состава в предельном случае
% Автор: студент ДГТУ группы У-3-47 В.В.Груздев < 21.05.02 >
clc;clear;
disp('Вектор запасов на текущий год');
n=[300 100 50]
disp('Вектор вероятнотей ухода (увольнение или что-либо еще)');
w=[0.2 0.1 0.2]
disp('Вектор, определяющий распределение нанимаемых по классам');
r=[0.75 0.25 0]
disp('Матрица вероятностей переходов, управляющая перемещениями в системе')
P=[0.6 0.2 0;
0 0.7 0.2;
0 0 0.8]
% Вероятностная матрица (матрица Маркова)
Q=P+w'*r;
disp('В случае t=infinity определим матрицу Qt=Q^infinity.');
disp('У нее все строки будут равными.Строку обозначим q.');
siz=length(n);
A=(Q-eye(siz))';
A=[A(1:siz-1,:); ones(1,siz)];
b=zeros(siz,1);b(siz)=1;
q=(inv(A)*b)'
Qinf=[];
for I=1:siz, Qinf=[Qinf;q]; end
disp('Вектор запасов в бесконечности - насыщение');
ninf=n*Qinf
Список использованной литературы
1) Задачи по математическому моделированию. Сборник. 1979.
2) Розанов Ю.А. Случайные процессы. Краткий курс.— М.: Наука, 1971.
3) Гнеденко Б.В. Курс теории вероятностей.— М.: Наука, 1988.
|
|
|
