 |
Передаточные функции систем автоматического управления
|
|
|
|
Операторная форма записи дифференциального уравнения. Передаточная функция.
Динамика функциональных элементов и систем управления описывается дифференциальным уравнением, которое в общем виде можно записать как
1.15
Необходимо, чтобы n >m, для работы системы. Описание существенно упрощается если от дифференциального уравнения перейти к операторной форме. Для этого необходимо операцию дифференцирования заменить на оператор дифференцирования
р1 – оператор дифференцирования
В результате такой замены мы получили алгебраическое уравнение
1.16
Если в уравнении (1.15) вместо функции времени у(t) и х(t) ввести функции х(р) и у(р) комплексного переменного р=α±jβ, поставив условием что записанные функции связаны отношением
1.17
то оказывается что дифференциальное уравнение, содержащие х(t) и у(t) равносильно алгебраическому уравнению вида
1.18
Следует отметить, что трансформация дифференциального уравнения в представленное алгебраическое возможно только при нулевых начальных условиях. И это преобразование в математике называют преобразованием Лапласа. Функции х(р) и у(р) называют изображениями функций х(t) и у(t), а сами функции х(t) и у(t) называют оригиналами функций х(р) и у(р).
Переход от искомой функции у(t) к изображению у(р) называют прямым преобразованием Лапласа, и обозначают
1.19
Переход же от изображения у(р) к оригиналу у(t) называют обратным преобразованием Лапласа
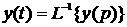1.20
Из сравнения уравнений (1.18) и (1.16) видно, что обе формы записи совпадают, из чего следует, что оператор дифференцирования отождествляется с комплексной переменной р при нулевых начальных условиях.
|
|
|
Использование операторной формы представления уравнений позволяет избежать решения дифференциальных уравнений путем решения системы алгебраических уравнений. Нахождение оригиналов по изображениям можно провести используя либо справочные таблицы, либо формулу разложения.
Взяв за основу формулу (1.18) можно найти отношение
1.21
Передаточной функцией W(р) называют отношение изображения по Лапласу выходной величины к изображению входной величины при нулевых начальных условиях.
Из уравнения (1.21) можно записать
1.22
Многочлен, фигурирующий в знаменателе передаточной функции называется характеристическим многочленом, а в случае приравнивания его у нулю уравнение называется характеристическим.
1.23
Корни характеристического уравнения называют полюсами передаточной функции. Корни многочлена, расположенного в числителе передаточной функции, называют нулями передаточной функции.
Передаточные функции систем автоматического управления
Записанные выше дифференциальные уравнения системы автоматического управления (5.4) и (5.6) могут быть получены также на основании понятия передаточной функции, которое было введено в главе 3. Рассмотрим рис. 5.1, где изображена замкнутая система автоматического управления.
Предположим вначале, что чувствительный элемент (ЧЭ) отсоединен от управляемого объекта (УО), и рассмотрим так называемую разомкнутую систему автоматического управления.
Управляющее воздействие, которое прикладывается к управляемому объекту, определяется выражением
— передаточная функция управляющего устройства, которая определяется из дифференциального уравнения управляющего устройства (5.2):
Управляемая величина может быть найдена из выражения
—
передаточная функция объекта по
Первая из них определяется из дифференциального уравнения объекта (5.1) при
|
|
|
Передаточную функцию разомкнутой системы можно определить как отношение изображений управляемой величины и ошибки при нулевых начальных значениях и возмущающих воздействиях, равных нулю:
— комплексная величина.
в разомкнутой системе:
— оператор дифференцирования.
Учитывая (5.13), формулу (5.15) можно также записать в виде
Передаточная функция разомкнутой системы имеет весьма большое значение в теории автоматического управления, так как многие методы анализа и синтеза основаны на использовании именно этой функции.
Решая (5.12) и (5.17) совместно, получаем для управляемой величины
и для ошибки
называется передаточной функцией замкнутой системы. Она устанавливает связь между управляемой величиной и задающим воздействием при равенстве пулю возмущающих воздействий:
называют передаточной функцией замкнутой системы по ошибке. Оно дает связь
между ошибкой и задающим воздействием в замкнутой системе при равенстве нулю возмущающих воздействий:
при нулевых начальных условиях и отсутствии внешних возмущений:
также при пулевых начальных условиях и отсутствии внешних возмущений.
раз по сравнению с отклонением в разомкнутой системе (5.12).
когда цепь управления разорвана и автоматическое управление отсутствует.
представляет собой полином знаменателя передаточной функции замкнутой системы:
)
Он равен сумме полиномов числителя и знаменателя передаточной функции разомкнутой системы (5.13).
Приравнивание нулю характеристического полинома (5.24) дает характеристическое уравнение замкнутой системы;
Оно может быть записано в более удобной форме, которая непосредственно получается из (5.18) или (5.19):
Полином знаменателя передаточной функции разомкнутой системы С(р) представляет собой характеристический полином разомкнутой системы.
Из рассмотренного видно, что знание передаточной функции разомкнутой системы позволяет найти выражение для ошибки и управляемой величины в функции задающего и возмущающих воздействий, а также характеристическое уравнение системы.
Передаточная функция разомкнутой системы может находиться непосредственно по структурной схеме и передаточным функциям входящих в нее звеньев.
|
|
|
|
|
|
