 |
2. Математическая база предпочтительных чисел
|
|
|
|
2. МАТЕМАТИЧЕСКАЯ БАЗА ПРЕДПОЧТИТЕЛЬНЫХ ЧИСЕЛ
Предпочтительные числа образуют ряды чисел, которые подчиняются строго определенной математической закономерности. Наиболее целесообразно в качестве математической закономерности использовать арифметические или геометрические прогрессии.
Арифметические прогрессии весьма просты. В них разность между двумя соседними членами остается постоянной во всем диапазоне.
Nn – Nn-1 = d (1),
где Nn и Nn-1 — значения рядом стоящих членов ряда;
d — разность прогрессии.
Однако арифметические прогрессии имеют существенный недостаток: относительную неравномерность. При постоянной абсолютной разности относительная разность между членами ряда резко уменьшается. Так, относительная разность между членами арифметической прогрессии 1—2—3—4.. . 9 – 10... 99—100 для чисел 1—2 составляет 100%, для 9—10 составляет 11%, а для чисел 99—100 всего 1%. Если такую прогрессию использовать для построения параметрических рядов, то это приведет к относительному сгущению рядов по мере роста членов ряда. В конечном итоге увеличится количество больших значений параметров по сравнению с количеством малых значений.
Ряды, построенные по арифметической прогрессии, в стандартизации используют редко, однако такие стандарты есть. Например, стандарты на диаметры подшипников, на размеры обуви, одежды и др.
Для того, чтобы частично устранить относительную неравномерность рядов используют для построения рядов предпочтительных чисел ступенчато—арифметическую прогрессию. Для нее характерно, что разность двух соседних членов ряда постоянна не для всего ряда, а только для определенной его части.
|
|
|
Ступенчато—арифметические прогрессии применимы, например, в стандартах на размеры болтов, винтов, шпилек, классов точности приборов, оптической силы очковых линз.
Специальные исследования показали, что наиболее удобны для стандартизации геометрические прогрессии.
Геометрической прогрессией называется последовательность чисел, в которой отношение двух соседних членов величина постоянная.
g = Nn / Nn-1 (2),
где Nn и Nn-1 — значения рядом стоящих членов ряда;
g — знаменатель прогрессии.
Геометрические прогрессии имеют ряд полезных свойств, успешно используемых в стандартизации. Назовем основные из кних:
1) относительная разность между любыми соседними членами ряда постоянна, следовательно, геометрическая прогрессия равномерна;
2) произведение или частное любых членов прогрессии является членом той же прогрессии. Это свойство используется при увязке между собой стандартизуемых параметров в пределах одного ряда предпочтительных чисел.
Однако на базе геометрических прогрессий можно построить бесконечное множество рядов чисел с различимыми знаменателями. Из них нужно выбрать такие, которые будут иметь преимущества перед остальными. Оказывается, что более всего отвечают требованиям стандартизации геометрические прогрессии, включающие единицу имеющие знаменатель вида g = 
 , где R — целое число. Как увидим дальше, для системы предпочтительных чисел отобраны показатели степени 5; 10; 20; 40; 80; 160.
, где R — целое число. Как увидим дальше, для системы предпочтительных чисел отобраны показатели степени 5; 10; 20; 40; 80; 160.
3. СВОЙСТВА ОСНОВНЫХ РЯДОВ ПРЕДПОЧТИТЕЛЬНЫХ ЧИСЕЛ
ГОСТ 8032—84 “Предпочтительные числа и ряды предпочтительных чисел устанавливает четыре основных ряда предпочтительных чисел R5; R10; R20; R40 и два дополнительных R80; R160. Применение последних допускается только в отдельных, технически обоснованных случаях.
Государственный стандарт регламентирует установленные округленные значения как знаменателей прогрессии, так и членов всех рядов предпочтительных чисел.
|
|
|
Перечислим некоторые свойства основных рядов предпочтительных чисел:
1) ГОСТ 8032—84 устанавливает стандартные значения предпочтительных чисел в диапазоне 0< a< ∞ на основе фиксированных величин включенных в десятичный интервал 1< a≤ 10. Все зти числа в десятичном интервале от 1 до 10 приведены в табл. 1;
2) для перехода от предпочтительных чисел, таблица 1, в любой другой десятичный интервал нужно умножить эти числа на 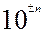 , где
, где
n — целое число, так при n = -1 числа переходят в интервал 0, 1< a< 1;
3) для получения значений предпочтительных чисел каждого ряда нужно умножить единицу (вспомним требование: ряды предпочтительных чисел должны включать единицу) на соответствующий знаменатель прогрессии ряда. Дальнейшее последовательное умножение найденных чисел на знаменатель прогрессии и округление полученных значений приведет к одному из рядов. Например, для ряда R 5 первый член — 1, знаменатель прогрессии g = 1, 60. Тогда второй член равен 1 ·1, 60 = 1, 60, третий – 1, 60 ∙ 1, 60 ≈ 2, 50 и т. д.;
4) номер ряда предпочтительных чисел R 5, R10; R20; R40 указывает на количество чисел в десятичном интервале. Принято называть ряды с большим знаменателем и меньшим числом членов разряженными, а ряды с меньшим знаменателем и большим числом членов — густыми;
Таблица 1 - Основные ряды предпочтительных чисел по ГОСТ 8032-84
| Основные ряды | Номер числа в интервале [1-10] | Мантисса десятичного логарифма | |||
| R5 g=1. 60 | R10 g=1. 25 | R20 g=1. 12 | R40 g=1. 06 | ||
| 1, 00 1, 60 2, 50 4, 00 6, 30 10, 00 | 1, 00 1, 25 1, 60 2, 00 2, 50 3, 15 4, 00 5, 00 6, 30 8, 00 10, 00 | 1, 00 1, 12 1, 25 1, 40 1, 60 1, 80 2, 00 2, 24 2, 50 2, 80 3, 15 3, 55 4, 00 4, 50 5, 00 5, 60 6, 30 7, 10 8, 00 9, 00 10, 00 | 1, 00 1, 06 1, 12 1, 18 1, 25 1, 32 1, 40 1, 50 1, 60 1, 70 1, 80 1, 90 2, 00 2, 12 2, 24 2, 36 2, 50 2, 65 2, 80 3, 00 3, 15 3, 35 3, 55 3, 75 4, 00 4, 25 4, 50 4, 75 5, 00 5, 30 5, 60 6, 00 6, 30 6, 70 7, 10 7, 50 8, 00 8, 50 9, 00 9, 50 10, 00 | ||
5) среди чисел таблицы 1 есть число 3, 15, которое стандартизаторы используют в своей практике в качестве числа π = 3, I416. Использование при расчетах числа π позволяет выражать предпочтительными числами длины окружностей, площади кругов, скорости резания, цилиндрические и сферические поверхности и объемы.
|
|
|
Если выразить диаметр окружности d предпочтительным числом ряда R40 и умножить это число на другое предпочтительное число 3, 15, то длина окружности l=π d будет представлена предпочтительным числом того же ряда;
6) в практике стандартизации следует предпочитать каждому предпочитать ряду предыдущий ряд. Ряд R5 следует предпочитать ряду R10, R10 – ряду R20 и т. д.;
7) в таблице 1 все предпочтительные числа имеют номера от 0 до 40.
Эти номера облегчают расчеты взаимосвязанных показателей стандартов, ускоряют вычисления. Номера чисел N представляют собой логарифмы предпочтительных чисел а при основании логарифмов, равном знаменателю прогрессии g
|
|
|


