 |
N = logga (3). 4. Выборочные и составные ряды предпочтительных чисел. 5. Приближенные предпочтительные ряды
|
|
|
|
N = logga (3)
В практике вычислений для упрощения расчетов используется известное свойство логарифмов, позволяющее вместо умножения или деления самих предпочтительных чисел складывать или соответственно вычитать номера этих чисел, а по результирующему номеру определять искомое число.
Например, необходимо перемножить предпочтительные числа 2, 24 и 3, 55, то получим 7, 952; результат требуется округлить, подвести его к стандартному значению 8, 00. При пользовании же номерами предпочтительных чисел (см. таблицу 1) достаточно провести сложение:
N = N 2, 24 + N 3, 55 = 14 + 22 = 36
Под номером 36 значится стандартное число 8, 00.
Возведение предпочтительного числа в целую положительную или отрицательную степень производят путем умножения порядкового номера предпочтительного числа на показатель степени с последующим нахождением в таблице 1 числа, соответствующего полученному порядковому номеру. Например: 3, I5², 2N 3, 15 = 2 · 20 = 40. Номеру 40 соответствует число 10.
Если учесть, что при умножения предпочтительного числа табл. 1 на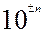 
в новом числе запятая оказывается перенесенной на n знаков (вправо при +n или влево при -n), номер нового числа можно определить по формуле:
N = Nт ± n · 40, (4)
где Nт - номер числа в таблице 1
4. ВЫБОРОЧНЫЕ И СОСТАВНЫЕ РЯДЫ ПРЕДПОЧТИТЕЛЬНЫХ ЧИСЕЛ
Приведенные выше обозначения рядов (R5; R10; R20; R40; R80; R160) характеризуют ряды не ограниченные никакими пределами.
В практике конструирования, как правило, применяются ряди с ограниченными пределами. Такие ряды обозначаются: R 20 (160... 280) — основной ряд R20, ограниченный членом 160 в качестве нижнего предела и членом 280 в качестве верхнего предела. Пользуясь таблицей 1 запишем в развернутом виде последний ряд чисел:
|
|
|
160-180-200-224-250-280
В стандартизация используют также выборочные ряды. Они применяются в тех случаях, когда ни одна из градаций основных рядов не удовлетворяет поставленным требованиям. Обычно по выборочным рядам строят ряда параметров и размеров являющихся функциями других параметров и размеров, для которых градации приняты по основным рядам. Выборочные ряды образуются из основных или дополнительных путем отбора n-го члена ряда, начиная с любого числа ряда.
Обозначение выборочного ряда состоит из обозначения исходного основного ряда, после которого ставится косая черта и число 2; 3; 4... n соответственно.
Если ряд ограничен, обозначение должно содержать члены, ограничивающие ряд; если ряд не ограничен, должен быть указан хотя бы один его член.
Например, R40/5 (... 60) — выборочный ряд, полученный путем отбора каждого пятого члена основного ряда R40 и ограниченный членом 60 в качестве верхнего предела.
Допускается использовать составные ряды, построенные из разных основных и выборочных рядов. Например: 1, 0 — I, 6 — 2, 5 — 4, 0 — 6, 3 — 8, 0 — 10, 0. Этот составной ряд составлен из двух рядов: R5 (1, 0... ... б, 3) и R10 (6, 3 … 10, 0). Конечные и начальные члены смежных рядов, образующих составной ряд, должны быть одинаковыми. Составные ряды применяются, если требуемая плотность значений параметра в рассматриваемом интервале неодинакова.
5. ПРИБЛИЖЕННЫЕ ПРЕДПОЧТИТЕЛЬНЫЕ РЯДЫ
Предпочтительные числа, включенные в ГОСТ 8032—84 как уже отмечалось, являются округленными по сравнению с расчетными членами геометрических прогрессий. Однако, как показала практика, в отдельных случаях требуются дополнительные округления стандартизованных чисел. Например, при установлении числа зубьев шестерен нельзя использовать число 31, 5 (типичным может быть 32) или нецелесообразно требовать времени экспозиции для фотоаппаратов 1/31, 5 с вместо более простого значения 1/30 (число 3, 00 отсутствует в рядах R5; R10; R20).
|
|
|
ГОСТ 8032—84 в обоснованных случаях допускает применять вместо основных рядов R ряды R' и R'' приближенных предпочтительных чисел. В ряду R' отдельные предпочтительные числа ряда R заменены величинами первой степени округления, в ряду R'' — второй степени округления.
В альтернативных ситуациях следует отдавать предпочтение числам из ряда R перед числами R', а числам R' перед числами R''. Включение приближенных предпочтительных чисел в дополнительные ряды не допускается.
Перечислим приближенные предпочтительные числа рядов R' и R'', отличающиеся от чисел соответствующего основного ряда.
В ряд R'' 5 входят числа 1, 5 и 6, 0, соответствующие числам 1, 6 и 6, 3 ряда R5.
Ряд R'10 идентичен ряду R10, за исключением члена 3, 15, который заменен членом 3, 20.
Ряд R'' I0 содержит числа: 1, 2; 1, 5; 3, 0; 6, 0 (в ряду R''10 они заменяют ближайшие числа ряда R10; далее аналогичные замены).
Вряд R'20 входят числа: 1, 1; 2, 2; 3, 2; 3, 6, а в ряд R'' 20 — 1, 2; 3, 0; 3, 5; 5, 5; 6, 0; 7, 0.
В ряд R'40 — 1, 05; 1, 1; 1, 2; 1, 3; 2, 1; 2, 2; 2, 4; 2, 6; 3, 2; 3, 4; 3, 6; 3, 8; 4, 2; 4, 8.
|
|
|
