 |
Численное интегрирование (блок NUMINT)
|
|
|
|
Для начала динамического расчета необходимо задать параметры численного интегрирования в блоке NUMINT. Указываем номер интегрирования 1. Если мы повторяем расчет и номер 1 уже существует, командой «-1» можно удалить предыдущий расчет. Можно также указывать каждый раз новый номер интегрирования (1, 2, 3 и т.д.), не удаляя предыдущий.
Затем указываем название, начальное и конечное время интегрирования, интервал времени для сохранения результатов.
‘Oscillations’ 0. 8. 0.01
Указывать метод интегрирования, максимальный или минимальный шаг интегрирования, значение степени точности, максимальное количество вызовов оценки функции нет необходимости, т.к. данные параметры не влияют на расчет. Но в качестве примера можно указать значения перечисленных выше параметров, используемых для модели движения вагона по рельсам.
8 0.05 -5 99999999 1 0
Вывод результатов численного интегрирования (блок AUSINT)
С помощью данного блока полученные результаты численного интегрирования можно вывести на экран или в отдельный файл. В случае вывода результатов в файл, создается файл (plot/plot####.nnn), где nnn – его порядковый номер, например 000, 001 и т.д. Он читается программой «Diamed», которая находится в корневом каталоге MEDYNA. «Diamed» позволяет выбрать те числовые массивы, которые необходимы, и создать файл, читаемый стандартными программами, производящими вычислительные операции, такими как Microsoft Excel.
Примеры получения результатов собственных и вынужденных колебаний из динамической модели программного комплекса MEDYNA
График свободных колебаний кузова порожнего вагона, полученный при выведении системы из состояния покоя силовым импульсом величиной A1=300 кН, с жесткостью подвешивания C=4МН/м и коэффициентом вязкого трения β 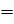 118,3
118,3  кг/сек. представлен на рисунке 9.
кг/сек. представлен на рисунке 9.
|
|
|

Рисунок 9 – График собственных колебаний кузова порожнего вагона
График вынужденных колебаний кузова порожнего вагона, полученный при наложении на систему синусоидального импульса величиной A1=300 кН, с жесткостью подвешивания C=4МН/м, коэффициентом вязкого трения β 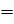 118,3
118,3  кг/сек. и циклической частотой ω=6,28 рад/сек представлен на рисунке
кг/сек. и циклической частотой ω=6,28 рад/сек представлен на рисунке 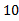 .
.

Рисунок 10 – График вынужденных колебаний кузова порожнего вагона
Формулирование выводов
Проанализировать влияния жесткости подвешивания и коэффициента вязкого трения гасителя колебаний на собственные (данные для анализа представлены в таблицах 8-9) и вынужденные (таблицы 10) колебания для порожнего вагона. Дополнительно произвести оценку влияния циклической частоты вынужденных колебаний ω на характер колебательного процесса.
Таблица 8 – Изменение жесткости подвешивания для свободных колебаний
| № | Жесткость подвешивания, МН/м | Коэффициент вязкого трения, кг/сек |
1 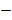 3 3
| 1 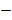 5 5
| 60 
|
Таблица 9 – Изменение коэффициента вязкого трения для свободных колебаний
| № | Жесткость подвешивания, МН/м | Коэффициент вязкого трения, кг/сек |
1 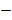 3 3
| 10  60 60 
|
Таблица 10 – Изменение жесткости подвешивания для вынужденных колебаний
| № | Жесткость подвешивания, МН/м | Коэффициент вязкого трения, кг/сек | Циклическая частота, рад/сек |
1 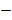 3 3
| 1 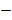 5 5
| 60 
| π 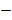 4π 4π
|
Проанализировать влияние загруженности вагона (тара и брутто) на характер колебательного процесса при определенной жесткости и коэффициенте демпфирования.
Подвести итог влияния жесткости рессорного подвешивания, коэффициента вязкого трения гасителя колебаний и массы кузова вагона на интенсивность колебательного процесса. Обратить внимание на прогибы подвешивания. Привести в выводах графики колебаний кузова вагона, полученные в программном комплексе MEDYNA.
|
|
|
|
|
|


