 |
Особые случаи симплексного метода
|
|
|
|
Не единственность оптимального решения (альтернативный оптимум)
Рассмотрим задачу:
При решении задачи геометрически, мы убедились, что оптимум достигается на отрезке, принадлежащем прямой 
Рассмотрим этот вариант при симплекс-методе. На очередном шаге получим:
| Базис | Свободный | Переменные | Оценочные | ||||
| член | отношения | ||||||
| 
| 
| 
| 
| |||
|
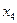
| 2/3 | 1/3 | |||||
|
| 1/3 | -1/3 | 
| ||||
|
| |||||||
|
Здесь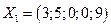 
- допустимое решение и соответствует точке (3; 5) на графике. Критерий оптимальности выполнен, следовательно 
-оптимальное решение и максимальное значение функции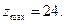 
Однако в оценочной строке коэффициент перед небазисной переменной 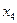равен нулю, поэтому изменение этой переменной не повлечет изменение целевой функции, следовательно, ее можно внести в основные переменные.
| Базис | Свободный | Переменные | ||||
| член | ||||||
|
|
|
|
|
| ||
|
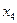
| 1/3 | -1/3 | ||||
|
| 2/3 | 1/3 | ||||
|
| ||||||
|
|
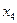
Получим 
- оптимальное решение и 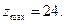Данному решению соответствует точка (6; 2) на графике.
Учитывая, что переменная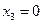 
в базисном решении 
стается не основной, а удовлетворяет неравенству 
, можно получить все множество оптимальных решений.
Пусть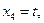 
. Имеем
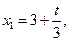
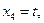
Замечании. Множество решений можно представить как выпуклую линейную комбинацию базисных решений
Появление вырожденного базисного решения
Рассмотрим задачу:
Решим задачу симплексным методом. Введем дополнительные переменные и составим симплекс-таблицу.
|
|
|
| Базис | Свободный | Переменные | Оценочные | ||||
| член | отношения | ||||||
|
|
|
|
|
| |||
|
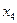
| -1 | ||||||
|
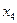
| -2 | ||||||
| -4 | 7/3 | |||||
|
| -2 |
Так как полученное решение 
не оптимально, переходим к новой симплекс-таблице. Причем, в качестве разрешающей строки можно взять как первую, так и вторую.
| Базис | Свободный | Переменные | Оценочные | ||||
| член | отношения | ||||||
|
|
|
|
|
| |||
|
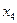
| -1 |
| |||||
|
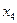
| -3 | ||||||
|
| -б | ||||||
|
| -1 | ! |
Полученное решение 
вырожденно, так как основная переменная 
и вновь не является оптимальным. Переходим к новой симплекс-таблице.
| Базис | Свободный | Переменные | Оценочные | ||||
| член | отношения | ||||||
|
|
|
|
|
| |||
|
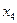
| -2 | ||||||
|
| -3 | ||||||
|
| -2 | ||||||
|
| -1 |
Решение 
так же вырожденно, так как основная компонента 
При этом целевая функция не увеличилась, но и не ухудшилась. Выполненный шаг, хотя и не улучшил значение целевой функции, лишнем не является, так как привел к новому базисному решению. На практике, наличие пустых шагов может привести к зацикливанию задачи.
Вывод. Если на каком-либо шаге симплекс-метода наибольшее возможное значение переменной достигается в нескольких уравнениях одновременно, то в качестве разрешающего можно выбрать одно из них (в симплекс-таблице совпадение оптимальных оценочных отношений). Тогда на следующем шаге получим вырожденное базисное решение, переход к очередному базисному решению может не изменить значение целевой функции.
Замечание. Вырождение, полученное при оптимальном решении может привести к альтернативному оптимуму даже при нулевых коэффициентах при всех не основных переменных в целевой функции.
|
|
|
Отсутствие конечного оптимума.
Рассмотрим задачу:
При геометрическом решении убеждаемся, что оптимум отсутствует. Рассмотрим симплекс-метод на очередном шаге:
| Базис | Свободный | Переменные | Оценочные | ||||
| член | отношения | ||||||
|
|
|
|
|
| |||
|
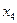
| 5/3 | -1/3 | -1/3 |
| |||
|
| 7/3 | -2/3 | 1/3 |
| |||
|
| -1 |
| |||||
|
| -1/3 | -2/3 | 4/5 |
Условие оптимальности целевой функции не выполнено, так как в строке целевой функции коэффициент при 
. При попытке ввести в базис получаем 
. Уравнения не ограничивают рост следовательно, min не ограничен (не достигается).
Вывод: если на каком либо шаге получается, что во всех уравнениях системы (строках симплекс-таблице) бесконечные оценочные отношения той переменной, которая переводится в основные, то задача не имеет конечного оптимума.
|
|
|
