 |
Объективно обусловленные оценки и их смысл
|
|
|
|
Компоненты оптимального решения двойственной задачи называются оптимальными (двойственными ли объективно обусловленными) оценками исходной задачи.
| Число единиц продукции | Остатки ресурсов | |||||

| 
| 
| 
| 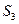
| 
| |

| 
| 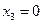
| 
| 
| 
| |

| 
| 
| 
| 
| 
| |
| превышение затрат на | объективно обусловленные оценки ресурсов | |||||
| ресурсы над ценой ресурса | (условные цены ресурсов) | |||||
Объективно обусловленные оценки ресурсов определяют степень дефицитности ресурсов по оптимальному плану производства. У дефицитных ресурсов объективно обусловленная оценка отлична от нуля, у недефицитных равна нулю. В рассматриваемом случаи ресурсы  и
и  расходуются полностью, т.е. являются дефицитными, а ресурсы
расходуются полностью, т.е. являются дефицитными, а ресурсы 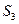 и
и  носят избыточный характер, т.е. в данном производственном цикле полностью не расходуются.
носят избыточный характер, т.е. в данном производственном цикле полностью не расходуются.
Рассмотрим превышение затрат на ресурсы над ценой ресурса. Если бы, например,  , то
, то  . И из этого следовало бы, что продукцию
. И из этого следовало бы, что продукцию  производить не выгодно, т.к. затраты на ресурсы превысили бы цену изготовляемой из них продукции. Следовательно, в оптимальный план производства могут попасть только рентабельные, неубыточные виды продукции.
производить не выгодно, т.к. затраты на ресурсы превысили бы цену изготовляемой из них продукции. Следовательно, в оптимальный план производства могут попасть только рентабельные, неубыточные виды продукции.
Третья теорема двойственности. Компоненты оптимального решения двойственной задачи равны значениям частных производных функции
 по соответствующим аргументам
по соответствующим аргументам 
Двойственные оценки могут служить инструментом анализа и принятия правильных решений в условиях постоянно меняющегося производства. Так, например, с помощью объективно обусловленных оценок ресурсов возможно сопоставление оптимальных условий затрат и результатов производства.
Пример. В результате решения задачи был получен оптимальный план 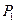 и
и  . Появилась возможность выпуска продукции
. Появилась возможность выпуска продукции  .Затраты каждого ресурса
.Затраты каждого ресурса  и
и  на выпуск этой продукции соответственно равны:
на выпуск этой продукции соответственно равны: 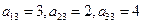 и
и  Цена продукции
Цена продукции  Даст ли прибыль включение в план дополнительной продукции? Имеем
Даст ли прибыль включение в план дополнительной продукции? Имеем
|
|
|
 и
и 
Сопоставим дополнительные затраты на ресурсы в расчете на единицу продукции  с ценой ее реализации:
с ценой ее реализации:
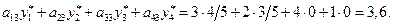
Полученный результат больше, чем цена продукции  Следовательно, ее выпуск не является рентабельным. Очевидно, чтобы включение новой продукции в производство было выгодно, надо, чтобы ее цена мыла не менее 3,6.
Следовательно, ее выпуск не является рентабельным. Очевидно, чтобы включение новой продукции в производство было выгодно, надо, чтобы ее цена мыла не менее 3,6.
Объективно обусловленные оценки ресурсов позволяют судить об эффекте не любых, а лишь сравнительно маленьких изменениях ресурсов. При крупных изменениях меняются сами оценки, что делает невозможным использование оценок для анализа производства.
Модели целочисленного линейного программирования
Если компонентами решения задачи линейного программирования должны быть целыми числами, то такая задача называется задачей целочисленного линейного программирования. В экономике это часто связанно с неделимостью продукции.



Существует несколько способов решения задач целочисленного линейного программирования.
Метод отсечения.
Суть метода состоит в том, что сначала решается задача линейного программирования без условия целочисленности. Если полученный ответ удовлетворяет условию целочисленности, то задача решена. В противном случае к ограничениям задачи добавляется новое ограничение, обладающее следующими свойствами:
- оно должно быть линейным;
- оно должно отсекать найденный оптимальный нецелочисленный план;
- оно не должно отсекать ни одного целочисленного плана.
Такие ограничения называются правильными отсечениями.
После введения нового ограничения вновь решается задача линейного программирования. Если вновь полученный план целочисленный то задача решена. Если это не так, то к задаче добавляется новое ограничение. Процесс повторяется до тех пор, пока полученный оптимальный план не будет полностью целочисленным.
|
|
|
Геометрический смысл добавления каждого нового линейного ограничения состоит в проведении дополнительной прямой (гиперплоскости), которая отсекает от многоугольника (многогранника) допустимых решений его часть вместе с оптимальной точкой с нецелыми координатами. В отсекаемую часть не должна попасть ни одна точка с целыми координатами. В результате новый многогранник решений содержит все точки с целыми координатами, содержавшиеся в первоначальном многограннике решений. Следовательно, полученное при этом многограннике оптимальное решение будет целочисленным.
Пример.

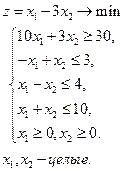
Построим область допустимых решений задачи. Это многоугольник АВСДЕ. Построим вектор градиент целевой функции  . Ясно, что точкой оптимума будет точка В(3.5; 6.5). Полученное решение не удовлетворяет условию целочисленности. Проведем прямую
. Ясно, что точкой оптимума будет точка В(3.5; 6.5). Полученное решение не удовлетворяет условию целочисленности. Проведем прямую  , отсекающую точку В и не отсекающую ни одну целую точку. Получаем новый многоугольник
, отсекающую точку В и не отсекающую ни одну целую точку. Получаем новый многоугольник  , где
, где  и
и  имеют целые координаты. Точка
имеют целые координаты. Точка 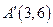 новое решение задачи целочисленного программирования.
новое решение задачи целочисленного программирования.
Метод Гомори.
Пусть задача линейного программирования имеет оптимальное решение. Не нарушая общности задачи предположим, что  - базисные переменные, полученные на последнем шаге симплекс-метода. Они выражены через небазисные переменные
- базисные переменные, полученные на последнем шаге симплекс-метода. Они выражены через небазисные переменные 


Оптимальное решение задачи 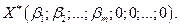
Пусть в этом оптимальном решении  - не целая компонента.
- не целая компонента.
Алгоритм метода Гомори
1. Решаем задачу симплекс методом. Если найденное решение целочисленно, то задача решена. Если задача не разрешима, то она не имеет решений и в целых числах.
2. Если среди компонент оптимального решения есть не целые, то надо выбрать компоненту с оптимальной целой частью и сформулировать правильное отсечение из условия 
3. Вводим дополнительную неотрицательную целую переменную  и получаем новое уравнение
и получаем новое уравнение 
4. Полученную расширенную задачу решаем симплекс-методом. Если новый найденный план целочисленный, то задача решена, если нет то повторяем процедуру.
Замечание.  - дробная часть числа
- дробная часть числа  .
.
Если задача разрешима в целых числах, то после конечного числа шагов (итераций) оптимальный целочисленный план будет найден. Если в процессе решения появится уравнение, выражающее основную переменную через неосновные, в котором свободный член не целый, а все остальные коэффициенты целые, то задача в целых числах решений не имеет. В симплекс таблице это условие соответствует тому, что в строке с нецелым свободным членом все остальные коэффициенты целые.
|
|
|
Пример. Решить задачу в целых числах.

Приведем задачу к каноническому виду:

Построим симплекс-таблицу
| Базис | Свободный | Переменные | Оценочные | ||||
| член | отношения | ||||||

| 
| 
| 
| 
| |||

| |||||||
| 17/2 | ||||||

| |||||||

| О | -2 | -3 |
Данный план не оптимален, так как в оценочной строке есть отрицательные элементы. Наибольший по модулю находится в столбце  . Следовательно
. Следовательно  переменная вводимая в базис. Построим оценочные отношения. Наименьшее соответствует строке
переменная вводимая в базис. Построим оценочные отношения. Наименьшее соответствует строке  . Значит
. Значит  вводимая в базис переменная. Переходим к новой симплекс-таблице.
вводимая в базис переменная. Переходим к новой симплекс-таблице.
| Базис | Свободный | Переменные | Оценочные | ||||
| член | отношения | ||||||

| 
| 
| 
| 
| |||

| -5 | 20/3 | |||||
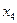
| -4 | 2/3 | |||||

| 
| ||||||

| -2 |
Полученное решение не является оптимальным.  вводимая,
вводимая, 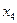 выводимая переменная. Переходим к новой симплекс-таблице
выводимая переменная. Переходим к новой симплекс-таблице
| Базис | Свободный | Переменные | Оценочные | ||||
| член | отношения | ||||||

| 
| 
| 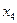
| 
| |||

| -1 | -1 | |||||

| 2/3 | 1/3 | -4/3 | ||||

| |||||||

| 76/3 | 2/3 | 1/3 |
Полученное решение  оптимально, но не является цело
оптимально, но не является цело
численным  .
.
Построим правильное отсечение из условия:

Найдем дробные части от чисел стоящих в фигурных скобках:

Получим неравенство

Введем дополнительную целую переменную 
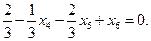
Полученное уравнение необходимо добавить в систему ограничений и решить
|
|
|
симплекс-методом новую задачу.
Для сокращения числа шагов можно вводить новое уравнение в симплекс-таблицу, полученную на последнем шаге.
| Базис | Свободный | Переменные | Оценочные | |||||
| член | отношения | |||||||

| 
| 
| 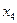
| 
| 
| |||

| -1 | -1 | 
| |||||

| 2/3 | 1/3 | -4/3 | 
| ||||

| ||||||||

| 2/3 | 1/3 | 2/3 | -1 | ||||

| 76/3 | 2/3 | 1/3 |
Полученное базисное решение не допустимо 
Замечание. Включение в систему ограничений дополнительного ограничения, соответствующего правильному отсечению всегда дает недопусти мое базисное решение.
Для получения допустимого базисного решения необходимо перевести в основные переменные переменную, входящую со знаком «+» в уравнение, в котором свободный член отрицательный. В рассматриваемом случае это переменная 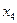 или
или  . Введем
. Введем  .
.
| Базис | Свободный | Переменные | Оценочные | |||||
| член | отношения | |||||||

| 
| 
| 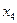
| 
| 
| |||

| -1/2 | -2/3 | ||||||
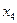
| -2 | |||||||

| -1/2 | 3/2 | ||||||

| 1/2 | 3/2 | ||||||

| 1/2 | 1/2 |
Полученное решение является оптимальным. Найденный план целочисленный 
Метод ветвей и границ.
Метод ветвей и границ - один из комбинированных методов решения задач целочисленного линейного программирования. Его суть состоит в упорядоченном переборе вариантов и рассмотрении лишь тех из них, которые оказываются по определенным признакам перспективными, и отбрасывании бесперспективных вариантов.
Метод ветвей и границ состоит в следующем: множество допустимых решений некоторым образом разбивается на подмножества, каждое из которых этим же способом разбивается еще на подмножества. Процесс продолжается до тех пор, пока не будет найден оптимальный план.
Пусть задача целочисленного линейного программирования решена симплекс-методом без учета целочисленности и известны верхняя и нижняя граница для каждой целой переменной 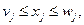
 и нижняя граница целевой функции
и нижняя граница целевой функции  :
:  для любого плана Х.
для любого плана Х.
Предположим, что компонента решения оптимального плана  не удовлетворяет условию целочисленности. Тогда из области допустимых решений исключается область
не удовлетворяет условию целочисленности. Тогда из области допустимых решений исключается область 
Начальная задача распадается на две (2) и (3). В задачу (2) добавится ограничение  , а в задачу (3) добавится ограничение
, а в задачу (3) добавится ограничение  .
.
Решаются задачи (2) и (3). В результате список задач может либо расшириться, либо уменьшиться. Если в результате решения задач (2) или (3) получаем нецелочисленный оптимальный план, при котором 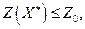 то эта задача исключается. Если
то эта задача исключается. Если  то из данной задачи формируются две новые.
то из данной задачи формируются две новые.
|
|
|
Если полученное решение  удовлетворяет условию целочисленности и
удовлетворяет условию целочисленности и  то значение
то значение  исправляется и за величину
исправляется и за величину  принимается оптимум линейной функции полученного оптимального целочисленного плана.
принимается оптимум линейной функции полученного оптимального целочисленного плана.
Процесс продолжается до тех пор, пока весь список задач не будет исчерпан, то есть все задачи будут решены.
Пример. Решить задачу в целых числах.

В качестве  принимаем значение целевой функции в точке
принимаем значение целевой функции в точке 

Решим задачу симплекс-методом. Получим 
 Так как первая компонента
Так как первая компонента  дробная, то из области допустимых решений исключим полосу
дробная, то из области допустимых решений исключим полосу  . Получим две задачи:
. Получим две задачи:
| Задача 2 | Задача 3 |



| 


|
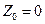
Решим задачу (3) симплекс-методом. Условия задачи (3) противоречивы. Решаем задачу (2). Имеем 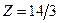
 Хотя
Хотя  по прежнему сохраняем
по прежнему сохраняем  так как план
так как план  не целочисленный. Величина
не целочисленный. Величина  -дробная, следовательно, исключаем полосу
-дробная, следовательно, исключаем полосу 
| Задача 3 | Задача 4 |



| 


|
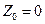
Решаем задачу (4). Имеем 
 Эту задачу исключаем из списка,
Эту задачу исключаем из списка,
но меняем  Решаем задачу (5). Имеем
Решаем задачу (5). Имеем 
 Значение
Значение  не меняем, так как план не целочисленный. Исключаем полосу
не меняем, так как план не целочисленный. Исключаем полосу 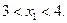 Получаем
Получаем
| Задача 6 | Задача 7 |

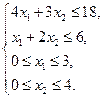

| 


|

Решаем задачу (7) симплекс-методом. Условия задачи (7) противоречивы. Решаем задачу (6). Имеем 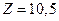
 Значение
Значение  следовательно, задача исключается из списка.
следовательно, задача исключается из списка.
Список задач полностью исчерпан. Получен оптимум 

|
|
|


