 |
Глава 4.Анализ результатов
|
|
|
|
4.1 Сравнение аналитической и имитационной моделей
Для проверки правильности построения имитационного алгоритма проведено сравнение результатов, полученных с использованием имитационной модели с аналитическим решением для упрощенной системы с меньшим числом реагентов и реакций, приведенным в статье [8]. Анализировалось две системы дифференциальных уравнений.
Аналитическая модель, которая сравнивалась с полученной имитационной дополнительно включает реакции блокировки,разблокировки и нуклеации с участием блокирующего протеина[8].
Для тестирования использованы начальные концентрации и скорости реакций, представленные в таблице 1[8,16].
Таблица 12. Начальные параметры, использованные для сравнения моделей (для неуказанных величин начальные значения равны нулю)
| Обозначение | Описание | Значение |
| скорость спонтанной нуклеации | 
|
| скорость элонгации плюс-конца | 
|
| скорость элонгации минус-конца | 
|
| скорость диссоциации плюс -конца | 
|
| скорость диссоциации минус -конца | 
|
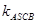
| скорость блокировки плюс-конца | 
|
| скорость разблокировки плюс-конца | 
|
| скорость нуклеации с участием блокирующего протеина | 
|
| концентрация g-актина | 
|
| концентрация блокирующего протеина | 
|
Результаты представлены на рисунке 4.
|
| |
а
| 
б
|
Рисунок 4-Сравнение результатов моделирования. Синие пунктиры –имитационная модель, красные звездочки– аналитическая модель. а – концентрация блокирующего протеина в филаментах (Сcap); б – концентрация f-актина (Сf);
В данном случае наблюдается практические эдентичные результаты, полученные с помощью двух моделей. Это связано с тем, что явления распада коротких филаментов практически не имеет место, в связи с активной нуклеацией и блокировкой филаментов.
|
|
|
Таким образом, полученные результаты позволяют сделать вывод о адекватности и правильности разработанной модели.
4.2 Анализ экспериментальных данных
Для изучения возможности использования разработанной модели для анализа экспериментальных данных,были изучены результаты экспериментов,представленные в статье[17]. В данном эксперименте был использован актин,извлеченный из скелетной мышцы килевидной грудной клетки. Были предварительно очищены g-актины в АТФ форме.В систему также был введен блокирующий протеин 
,извлеченный из кишечной палочки BL21 особым образом. Для изучения динамики процесса полимеризации использовалась силективная флуоресценция пирена.Таким образом в эксперименте были задействованы реакции элонгации,нуклеации,блокировки и разблокировки.По ходу эксперимента были получены скорости всех реакции. Предполагалось,что элогация происходит преимущественно на плюс конце филаменты,поэтому элонгация на минус-конце считается равной нулю,а в связи с активными процессами нуклеации и элонгации реакции диссциации также не были учтены. Все полученные в результате эксперимента данные представлены в таблице 2.
Таблица 2- Скорости реакции, полученные в результате эксперимента [17]
| Обозначение | Описание | Значение |
|
| скорость спонтанной нуклеации | 
|
|
| скорость элонгации плюс-конца | 
|
|
| скорость элонгации минус-конца |
|
|
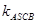
| скорость блокировки плюс-конца | 
|
|
| скорость разблокировки плюс-конца | 
|
|
| скорость нуклеации с участием блокирующего протеина | 
|
|
| концентрация g-актина | 
|
Данные из таблицы были использованы при имитационном моделировании и полученная концентрация f-актина была сравнена с результатами эксперимента (рисунок 5).
Рисунок 5-Сравнение результатов имитационного моделирования с результатами, полученными в результате эксперимента[29]
|
|
|
Таким образом, хорошая согласованность результатов позволяет сделать вывод о том, разработанная имитационная модель адекватна и соответствует реальным процессам полимеризации актина, происходящих в живых клетках и растворах.
Заключение
В работе построена имитационная модель процесса полимеризации актина, проведена верификация разработанной модели на аналитической модели и на экспериментальных данных. По результатам работы можно сделать следующие выводы:
· Блокирующий протеин не изменяет стационарного состояния f-актина, а ускоряет его достижение. Распределение филаментов по длинам меняется в сторону уменьшения при введении данного протеина в систему.
· Введение реакции фрагментации также не изменяет концентрации f-актина в стационарном состоянии, а лишь уменьшает среднюю длину филаментов в системе. Благодаря данной реакции филаментов становится больше в системе.
· Введение реакции старения актина в филаментах уменьшает значение стационарной концетрации f-актина и среднюю длину филаментов в системе, поскольку концы филаментов АДФ состоянии диссоциируют более интенсивно.
· Формин даже в небольших концентрациях значительно ускоряет наступление стационарного состояния. Значение концентрации f-актина в стационарном состоянии остается неизменным, за исключением случаев, когда концентрация формина становится на один порядок меньше начальной концентрации g-актина в АТФ форме. В таком случае наблюдается резкое снижение концентрации f-актина и момент достижения максимальной концентрации f-актина сдвигается по временной оси влево. При очень малых начальных концентрациях формина (порядка ~10^-4) наблюдается рост длин филаментов с увеличением концентрации формина. Однако, при дальнейшем увеличении концентрации наблюдается уменьшение их средней длинны.
· Наибольшим быстродействием обладает оптимизированный прямой метод Гиллеспи, поскольку при моделировании процесса полимеризации актина вероятности наступления различных реакций отличаются на несколько порядков, что позволяет использовать данный факт при оптимизации.
Построенную модель планируется в дальнейшем усовершенствовать и использовать для анализа экспериментальных данных, полученных с помощью FRAP- и флуоресцентной спектроскопии.
|
|
|
Список литературы к реферату
Список использованных источников
1. Soo, F.S. and J.A. Theriot, Large-scale quantitative analysis of sources of variation in the actin polymerization-based movement of Listeria monocytogenes. Biophys. J., 2005. 89(1): p. 703-23.
2. Alberts, J.B. and G.M. Odell, In silico reconstitution of Listeria propulsion exhibits nano-saltation. PLoS Biol., 2004. 2(12): p. e412.
3. Carlsson, A.E., M.A. Wear, and J.A. Cooper, End versus Side Branching by Arp2/3 Complex. Biophys. J., 2004. 86: p. 1074-81.
4. Yatskou, M.M., et al., Nonisotropic excitation energy transport in organized molecular systems: Monte Carlo simulation-based analysis of time-resolved fluorescence. J. Phys. Chem. A, 2001. 105(41): p. 9498-9508.
5. Nazarov, P.V., et al., FRET study of membrane proteins: simulation-based fitting for analysis of membrane protein embedment and association. Biophys. J., 2006. 91(2): p. 454-466.
6. Nazarov, P.V., et al., Artificial neural network modification of simulation-based fitting: application to a protein-lipid system. J. Chem. Inf. Comput. Sci., 2004. 44(2): p. 568-74.
7. Romero, S., et al., Formin is a processive motor that requires profilin to accelerate actin assembly and associated ATP hydrolysis. Cell, 2004. 119(3): p. 419-29.
8. Halavatyi,A, et al.,,. An integrative simulation model linking major biochemical reactions of actin-polymerization to structural properties of actin filaments.2008.p 1-6.
9. Gillespie, D.T., Approximate accelerated stochastic simulation of chemically reacting systems. J. Phys. Chem., 2001. 115(4): p. 1716-33.
10. Клячко, Н.Л. Биологическая подвижность и полимеризация актина,2000.с.2-4
11. Kovar, D.R., Molecular details of formin-mediated actin assembly. Curr. Opin. Cell Biol., 2006. 18(1): p. 11-7.
12. Gillespie, D.T., Exact stochastic simulation of coupled chemical reactions. J. Phys. Chem., 1977. 81(25): p. 2340-2361.
13. Gillespie, D.T., A general method for numerically simulating the stochastic time evolution of coupled chemical reactions. J. Comput. Phys., 1976. 22: p. 403-434.
14. Cao, Y., H. Li, and L. Petzold, Efficient formulation of the stochastic simulation algorithm for chemically reacting systems. J Chem Phys, 2004. 121(9): p. 4059-67.
15. Cao, Y., et al., The numerical stability of leaping methods for stochastic simulation of chemically reacting systems. J Chem Phys, 2004. 121(24): p. 12169-78.
16. Gibson, M.A. and J. Bruck, Efficient Exact Stochastic Simulation of Chemical Systems with Many Species and Many Channels. J. Phys. Chem., 2000. 104: p. 1876-89.
17. Pollard, T.D., Rate constants for the reactions of ATP- and ADP-actin with the ends of actin filaments. J Cell Biol, 1986. 103: p. 2747-54.
18. Carlsson, A.E., Actin Polymerization Overshoots and Hydrolysis as Assayed by Pyrene Fluorescence, 2008 p. 140-70.
19. Carlsson, A.E., Structure of Autocatalytically Branched Actin Solutions. PhysRevLett, 2004. 92(23): p. 238102-1-4.
Список публикаций соискателя
2. -А.Чухутина О.В. Имитационное моделирование биохимических реакций//Сборник работ 64-й научной конференции студентов и аспирантов Белгосуниверситета,2007.
|
|
|
3. -А.Чухутина О.В. Имитационное моделирование биохимических реакций//Материалы V республиканской научной конференции молодых ученых и студентов “Современные проблемы математики и вычислительной техники”,Брест,Беларусь,2007.
4. -А.Чухутина О.В. Построение и анализ имитационных моделей полимеризации актина//Сборник работ 65-й научной конференции студентов и аспирантов Белгосуниверситета,2008.
|
|
|
