 |
Задача №2. Расчёт рациональных маршрутов.
|
|
|
|
На конкретных примерах рассмотрим разработку маятниковых и кольцевых развозочных маршрутов со снабженческо-сбытовых баз и складов потребителям:
 А) Б² 2 ездки Бj Б2
А) Б² 2 ездки Бj Б2
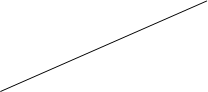



 7,5 км=1o=1o
7,5 км=1o=1o
LАБi=1АБ²=15,0км Г Бj Б²
13,0 км 6,0 км=1o=1o
А
1АБj=АБi=8км Бì 2 ездки
Б)
 Б¹ 6 км Г Lоб=103 км
Б¹ 6 км Г Lоб=103 км


 Lпор=57 км
Lпор=57 км
8 км 13 км Lгр=46 км
 15 км
15 км



 β=0,44
β=0,44
Б² LОб=97,5 км
Б¹ Г

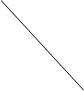

 В) Lпор=51,5 км
В) Lпор=51,5 км
13км 15 км Lгр=46 км
 |
Б² β=0, 47
Г-автохозяйство,А- база или склад, Бı Б² - потребители продукции.
Маятниковые маршруты с обратным холостым пробегом.При выполнении маятниковых маршрутов с обратным пробегом без груза возникает несколько вариантов движения автомобилей с разным по величине порожним пробегом. Необходимо разработать такой маршрут,при которой порожний пробег был бы минимальным.
|
|
|
На рисунке приведены условия перевозочной задачи, на примере решения которой составим маршрут движения автомобиля с минимальным порожним пробегом.
Из пункта А (база) необходимо доставить груз в пункты Бı и Б². Объём перевозок (в ездках) и расстояния указаны на рисунке.
За время в наряде автомобиль может выполнить на маршруте АБı=АБ² по две ездки с грузом.
Необходимо составить маршруты движения автомобилей, дающие минимум порожних пробегов.
Количество ездок определяется по формуле:
ne= —
где,Q- объём поставок продукции за рассматриваемый период, т.;
q- грузоподъёмность автомобиля,т.;γ –коэффициент использования грузоподъёмности в зависимости от класса груза.
При решении этой задачи могут возникнуть два варианта:
1.Продукция поставляется в в Б²,а потом в Бı,из Бı – в автохозяйство.
2.Продукция поставляется в в Бı,а потом в Б²,из Б² – в автохозяйство.
Как видим, из рисунка наиболее эффективен второй вариант,поскольку коэффициент использования β во втором случае выше,чем в первом.
Однако на практике при разработке маршрутов,руководствуясь правилом, чтобы уменьшить нулевой пробег,необходимо разрабатывать такую сис тему маршрутов,при которой первый пункт погрузки и последний пункт разгрузки находился вблизи от автохозяйства, мы склонны принять первый вариант.
Чтобы проверить правильность выбора,решим задачу математическим методом.
Задача составления рациональных маршрутов, обеспечивающих минимальный порожний пробег транспортных средств, сводится к следующей задаче линейного программирования:
Минимизируем линейную форму:
L=∑(lº-lабj)·Xj
При условиях 0≤ Xj ≤Qj и ∑ ≤Xj;
Пункты назначения пронумерованы в порядке возрастания разностей
|
|
|
(lo - lабj),т.е.
Lo – labl ≤ - lo – lАБ² ≤ lo – l аб3 ≤ …≤ lo – l АБn
Тогда оптимальное решение таково:
Х¹ = min (Q¹,N);
X² = min (Q²,N-X¹);
X³ = min (Q²,N-X¹-X²);
Xn = min (Q²N ∑ Xj)
Где lº -расстояние от пункта назначения до АТП (второй нулевой пробег); labj -расстояние от А до Б – гружёный пробег;N - число автомобилей, работающих на всех маршрутах; X j- количество автомобилей, работающих с последним пунктом разгрузки;A - поставщик(база); - Бj пункты потребления; Q m- объём перевозок(в ездках автомобиля).
Решая эту задачу,мы должны знать, что наилучшее решение получается при такой системе маршрутов, когда максимальное число автомобилей заканчивает работу в пунктах назначения с минимальными разностями,второго нулевого и гружёного пробега.
Для решения задачи необходимо исходные данные записать в специальную матрицу,чтобы с её помощью произвести все необходимые вычисления по составлению маршрутов. Для каждого пункта назначения, по каждой строке, рассчитывают алгебраические разности, которые записывают в соответствующие клетки столбца разностей.
Форма матрицы для составления оптимальных маятниковых маршрутов.
| Пункт назначения | Количество груженых ездок | разность |
| Б1 | loБ¹ Q¹ lАБ¹ | loБ¹-lАБ¹ |
| Б² | loБ² Q² lАБ² | loБ²-lАБ² |
| Бj | loБj Qj lАбj | loБj-lАБj |
| Бn | loБn Qn lАБn | loБn- l абn |
Рассмотрим применение предложенного алгоритма на конкретном примере,воспользовавшись исходными данными,приведёнными на рисунке.
Исходя из заданных условий составляем таблицы объёма перевозок и ездок (таблица 1) и расстояния перевозок (таблица 2).
Таблица 1
| Пункт отправления | Пункт назначения | |
| Б1 | Б² | |
| А | 2 | 2 |
Таблица2
| Пункт отправления и автохозяйство | Автохозяйство | Пункты назначения | |
| Бı | Б² | ||
| А | 13 | 8 | 15 |
| Г | - | 6 | 7,5 |
Для составления маршрутов определим время,необходимое для выполнения каждой едки АБ,используя формулы:
 te = +T n-p (1)
te = +T n-p (1)
*если данная гружённая ездка не является последней ездкой автомобиля;
|
|
|
 te = +Tn-p (2)
te = +Tn-p (2)
*если данная ездка выполняется автомобилем последней. Результаты этого расчёта сведены в таблице ниже:
Таблица №3
|
|
|


