 |
Тема: Плоская система произвольно расположенных сил
|
|
|
|
Задание 3
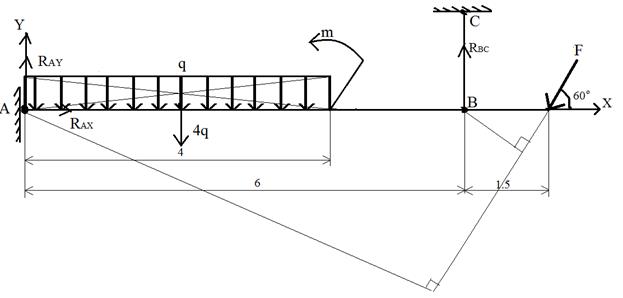
Брус, прикрепленный к опоре А и удерживаемый в равновесии стержнем ВС нагружен как показано на схеме, соединения в точках «А» и «С» шарнирные. Определить реакцию в опоре «А» и усилие в стержне ВС при следующих данных: F=30кН, q=15кн/м, m=45 кНм.
Решение:
1. Мысленно освобождаем брус от связей опоры «А» и стержня «ВС», заменив их действие на брус реакциями RAХ, RАУ, RВС.
2. Выбираем центр моментом (точки А) и координатные оси, совместив оси Х с осью бруса.
3. Составляем уравнения равновесия сил и определяем реакции в опоре «А» и стержне «ВС»
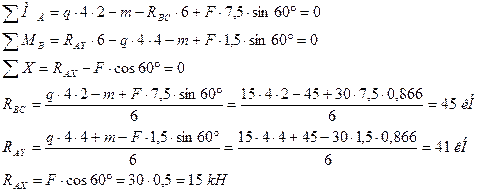
Если одну из реакций получим со знаком минус, то изменим её направление.
4. Определяем равнодействующую реакцию RAX и RAY.
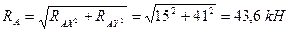
5. Проверка:
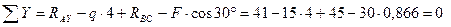
Результаты расчетов:
Таблица 1 ВкН
| № варианта | RAХ | RAY | RА | RBС |
| 43,6 |
Тема: Кинематика материальной точки
Методика решения задач
1. Устанавливаем траекторию и характер движения.
2. По соответствующим формулам определяем искомые величины.
Указание:
Обратите особое внимание на соблюдение размерностей.
Формулы по теме: кинематика материальной точки:
1. Равномерное прямолинейное движение:
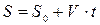
2. Равнопеременное прямолинейное движение:
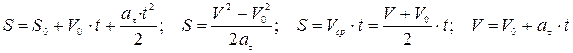3. Криволинейное движение:
плюс к формулам прямолинейного движения
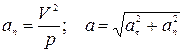
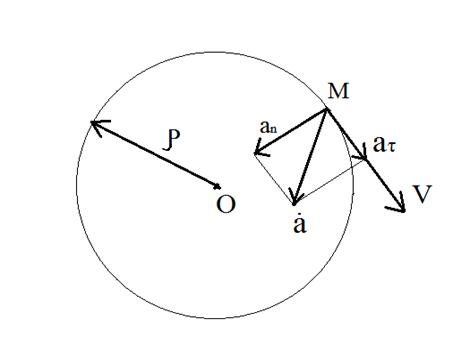
S – путь, м;
S0 – начально-пройденный путь, м;
V – скорость, м/с;
V0 – начальная скорость, м/с;
t – время, с;
aτ – касательное ускорение, м/с2;
an – нормальное (центростремительное) ускорение, м/с2;
a – полное ускорение, м/с2.
Задание 4
Материальная точка пришла в движение из состояния покоя по криволинейной траектории равноускоренно.
Когда точка прошла путь 344 м., ей сообщается нормальное ускорение 2,15 м/с2. Радиус кривизны траектории в этот момент 51 м.
|
|
|
Определить скорость в км/ч и полное ускорение в конце пути, а также время движения.
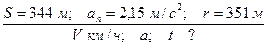
Решение:
1. Траектория криволинейная, движение равноускоренное.
2. Определяем скорость м.т.:
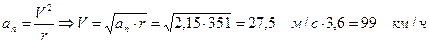
где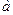 
n – нормальное ускорение, м/с;
V – линейная скорость, м/с;
r – радиус кривизны, м;
3. Определяем касательное ускорение:
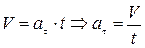
где t - время, с.
Так как время движения не известно, определяем его из уравнения:
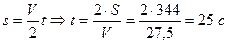
где S – путь, м.
Определив время движения, определяем касательное ускорение:
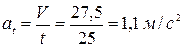
4. Определяем полное ускорение:
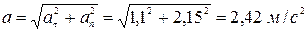
Ответы: V=99 км/ч;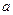 
=2,42 м/с2; t=25 с.
Тема: Вращательное движение твердого тела относительно неподвижной оси
Методика решения задач
1. Устанавливаем вид движения (равномерное или равнопеременное вращение)
2. По соответствующим формулам определяем искомые величины.
Указание: Обратить внимание на соблюдение размерностей.
Формулы по теме: Вращательное движение твердого тела:
1. Равномерное вращение:
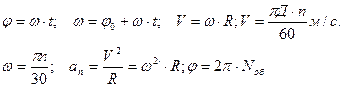
2. Равномерно-переменное вращение
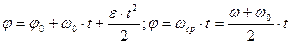
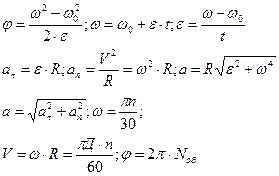
3. Передаточное отношение
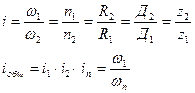
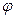- угол поворота, рад
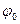- начальный угол поворота, рад
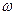- угловая скорость,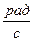 
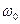- начальная угловая скорость,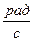
n – частота вращения, об/мин.
R – радиус, м.
Д – диаметр, м.
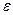- угловое ускорение,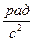 
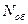- количество сделанных оборотов.
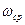- средняя угловая скорость,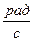
t – время, с.
Задание 5
Маховое колесо радиусом 500 мм требуется привести за 45 с из состояния покоя во вращательное движение с частотой вращения 300об/мин.
Определить какое угловое ускорение необходимо сообщить колесу, считая вращение в период разгона равноускоренным. Сколько оборотов сделает колесо за период разгона? Каковы будут скорость и ускорение точек обода колеса в конце периода?
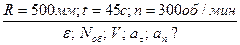
Решение:
1. Вращение равноускоренное
2. Определяем угловое ускорение, необходимое сообщить колесу в период разгона. 
|
|
|
где 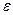– угловое ускорение, рад/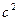 
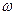– угловая скорость,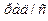 
t – время, с
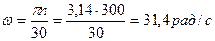
где n – частота вращения, об/мин.
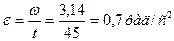
3. Определяем сколько оборотов сделает колесо за период разгона.
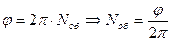
где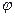 
- угол поворота в радианах
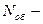число оборотов
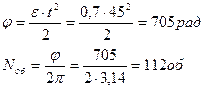
4. Определяем окружную скорость колеса в конце периода.
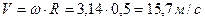
5.Определяем касательное ускорение колеса в конце периода.
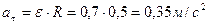
6.Определяем нормальное ускорение колеса в конце периода.
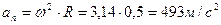
Ответы:
|
|
|
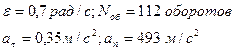
