Приемы работы при изучении системы счисления

 

Аналогичное положение существует и при изучении математики. Уже указывалось, что начальный курс математики может быть изучен быстрее и глубже, если он построен в соответствии с современными психологическими знаниями о возрастных возможностях детей, а также с учетом законов процесса усвоения.

Остановимся на начальных умениях, определяющих успех учащихся в овладении системой счисления.

Прежде всего отметим, что при изучении и этого предмета должна быть выделена основная (фундаментальная) система знаний и умений, которая и определяет успех начального математического образования.

В качестве примера рассмотрим экспериментальную программу, разработанную в Московском университете Н.Г. Салминой и В.П. Сохиной под руководством П.Я. Гальперина.

Одним из основных понятий этой программы является понятие меры, а одним из основных действий - измерение.

Если при обучении чтению до введения букв тщательно отрабатывается действие звукового анализа, то в курсе математики до введения чисел учащиеся усваивают измерение с использованием различного рода мер: простых и составных, больших и малых, для измерения дискретных и непрерывных величин.

Для обозначения результата измерения используются мет­ки (фишки, пуговки и т.п.).

Важным понятием является понятие величины. Выделение величин, подлежащих измерению, требует от детей умения выделять разные свойства в объектах. Вот почему изучение математики необходимо начинать с формирования этого ло­гического приема, если дети им не владеют.

Другое важное понятие, которое необходимо для овладе­ния действием измерения, - понятие о соответствии меры измеряемой величине (объем измеряется объемом, масса - мас­сой, протяженность - мерами протяженности, площадь - площадью и т.д.). В необходимости соблюдения этого требо­вания дети убеждаются практически: им предлагают, напри­мер, измерить кружку веревочкой. Аналогичным образом дети убеждаются и в необходимости меток. Им предлагается, например, измерить длину края стола (парты) с помощью счетной палочки. Работая без меток, дети не могут сказать, сколько раз уложилась мера в измеряемой величине. Посте­пенно, показывая практически необходимость выполнения целого ряда требований при измерении, учитель формулирует вместе с детьми правила измерения:

1. Выбор величины, которая будет измеряться.

2. Выбор меры для измерения.

3. Правило работы с мерой:

а) при измерении протяженности выбор точки, от ко­торой начинается измерение;

б) обозначение конечной точки каждого отмеривания;

в) в случае сыпучих тел - насыпание до краев.

4. Выкладывание метки после каждого измерения. (Если при последнем измерении мера не укладывается полностью - остается остаток.)

При выполнении каждого измерения учащиеся производят не только практические измерения, но и обязательно прого­варивают, с чего они будут начинать измерение, как его будут производить, фиксировать его результат и т.д.

После освоения действия измерения учащиеся усваивают действие сравнения двух величин. Здесь учащиеся осваивают действие установления взаимно-однозначного соответствия между двумя множествами. Необходимо показать, что срав­нивать величины можно только в том случае, когда они измерены одной и той же мерой. Предлагается, например, сравнить по объему две чашки крупы, которые резко различаются по величине. При этом крупу в маленькой чашке надо измерить маленькими чайными ложками, а в большой - большими столовыми. Дети получают два ряда меток, приводят их во взаимно-однозначное соответствие и видят: по меткам оказывается, что в маленькой чашечке крупы больше. Но очевидно, что это не так. И вот тут выясняется, почему получен неверный результат.

Можно использовать и такие величины (например, длину ленточек), которые не равны, а измерение разными мерами одно и то же число меток, т.е. получается, что ленточки одинаковой длины, а на самом деле они разные по длине. Ошибка очевидна. В дальнейшем это условие выполняется детьми очень строго.

Формирование понятий равно, не равно, больше, меньше идет успешней, если учитель предлагает не абстрактные задачи, не скучные отрезки и площади сами по себе, а облекает их в задачи, интересные для детей шести-семи лет. Например, учитель предлагает сравнить по длине дорожки, по которым бегают зверьки к ручейку пить. Дети могут разоблачить с помощью измерения хитрую лису, которая нечестно делила крупу с медведем и т. д.

Результат каждого сравнения, производимого детьми практически, руками, предстает перед ними в наглядном виде. Так, например, сравнивая по длине дорожки ежика и мышки, дети поучили такой результат:

 

Е

М

 

Очевидно, что дорожка ежика длиннее на три мерочки. Постепенно дети учатся записывать полученные результаты на математическом языке («переводят» на математический язык), употребляя буквы и математические знаки, отношения между двумя множествами (=, =, >, <).

Учащиеся сами получают последовательный ряд чисел, используя один и тот же способ: прибавление одной единицы к полученному числу. После введений чисел в пределах 10 учащиеся знакомятся с арифметическими действиями, с переместительным и сочетательным законами и на этой основе дета­льно изучают состав числа, раскладывая его на различные группы единиц. Большое внимание уделяется счету равными группами, что является подготовкой к введению умножения. Работа идет с использованием числовой оси. Для детей такой счет выступает как переход на более крупную меру.

Необходимость умножения доказывается учащимся через решение соответствующих задач. Например, предлагается узнать, сколько птичек можно накормить крупой, которая содержится в пакете. Каждой птичке нужна одна чайная ложка крупы.

Учащимся предлагается найти способы решения задачи. Ра­бота чайными ложками отвергается как длительная. Столовые ложки дают сравнительно быстро результат, но ответ на во­прос задачи остается не полученным. Обязательно кто-то из детей догадается: «Надо измерить, сколько чайных ложек вой­дет в столовую». Измеряют. Допустим, входят две ложки.

 

 

ст. л. ст. л.

 

Дети логично воспринимают умножение как изменение меры: брали сразу по две чайных ложки. И, допустим, брали такой мерой пять раз. Отсюда появляется запись 2х5=10.

Работали мелкими мерами (чайные ложки), но брали сразу по две таких меры.

Деление вводится как действие, обратное умножению: пере­ход на укрупненную меру. Допустим, есть 10 ложек крупы. На­до узнать, на сколько птичек хватит этой крупы, если каждая птичка съедает по две ложки. И надо знать, сколько раз содер­жится эта новая мера в измеряемом. Как видим, на основе меры и действия измерения можно показать детям и число, и дейст­вия с ним. Эти же понятия позволяют раскрыть перед учащи­мися различные системы счисления и позиционный принцип их построения. Каждый новый разряд системы счисления рас­сматривается как новая мера счета, а соотношения разрядов как соотношения мер, каждая из которых в определенное чис­ло раз больше, чем мера предыдущего разряда.Так, в деся­тичной системе 10 единиц первого разряда (единиц) дают единицу второго разряда (десятки) и т.д. Учащиеся сами об­разуют новые «меры счета», работая с разрядной сеткой.

 

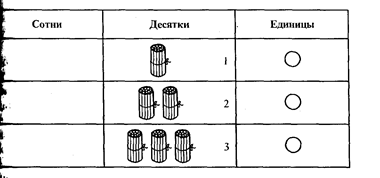
Так, единицы любого разряда считаются и записываются одинаково, поэтому дети легко начинают выполнять все арифметические действия с единицами любого разряда.

Позднее меры используются также при изучении десятичных и обыкновенных дробей. Следует отметить, что при таком подходе к построению курса начальной математики логичней вводить вначале десятичные дроби, а потом уже обыкновенные. Десятичные дроби выступают как вторая часть системы счисления, где мера при переходе от разряда в разряд не увеличивается, а наоборот, уменьшается. Обыкновенные дроби выступают перед учащимися тоже как переход на новую меру измере­ния, но теперь мера уменьшается не в десять, а в какое-то другое число раз. Характерно, что учащиеся, работающие по данным программам, никогда не допускают таких распространенных в школе ошибок при сложении дробей, как выполнение этого действия отдельно вначале на числителях, а затем - на знаменателях.

Работая с мерами, учащиеся с самого начала усваивают, что складывать и вычитать можно только измеренное одной и той же мерой. Поэтому, чтобы сложить 1/4 и 1/6, необходимо привести их к общей мере - к общему знаменателю.

Отметим, что многолетний опыт работы по данной программе показал, что принципы ее построения позволяют учащимся глубоко проникнуть в основы систем счисления, легко переходить из одной системы в другую. Одновременно это дает серьезное сокращение времени, необходимое для усвоения начального курса математики. Наконец, учет закономерностей усвоения и возрастных особенностей детей при разработке методики обучения позволяет обеспечить полноценное усвоение данного курса всеми учащимися.

Аналогичный подход - через выделение основополагающих понятий и действий - следует реализовать применительно и к умениям, обеспечивающим решение задач.

 

⇐ Предыдущая23242526272829303132Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: