 |
Методы изучения сезонных колебаний в рядах динамики.
|
|
|
|
Проверка гипотез о законе распределения
Обычно сущность проверки гипотезы о законе распределения ЭД заключается в следующем. Имеется выборка ЭД фиксированного объема, выбран или известен вид закона распределения генеральной совокупности. Необходимо оценить по этой выборке параметры закона, определить степень согласованности ЭД и выбранного закона распределения, в котором параметры заменены их оценками. Пока не будем касаться способов нахождения оценок параметров распределения, а рассмотрим только вопрос проверки согласованности распределений с использованием наиболее употребительных критериев.
Критерий хи-квадрат К. Пирсона
Использование этого критерия основано на применении такой меры (статистики) расхождения между теоретическим F (x) и эмпирическим распределением Fп (x), которая приближенно подчиняется закону распределения c 2. Гипотеза Н 0 о согласованности распределений проверяется путем анализа распределения этой статистики. Применение критерия требует построения статистического ряда.
Итак, пусть выборка представлена статистическим рядом с количеством разрядов y. Наблюдаемая частота попаданий в i -й разряд ni. В соответствии с теоретическим законом распределения ожидаемая частота попаданий в i -й разряд составляет Fi. Разность между наблюдаемой и ожидаемой частотой составит величину (n i – Fi). Для нахождения общей степени расхождения между F (x) и Fп (x) необходимо подсчитать взвешенную сумму квадратов разностей по всем разрядам статистического ряда
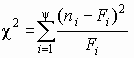 .
.
(3.7)
Величина c 2 при неограниченном увеличении n имеет распределение хи-квадрат (асимптотически распределена как хи-квадрат). Это распределение зависит от числа степеней свободы k, т.е. количества независимых значений слагаемых в выражении (3.7). Число степеней свободы равно числу y минус число линейных связей, наложенных на выборку. Одна связь существует в силу того, что любая частота может быть вычислена по совокупности частот в оставшихся y – 1 разрядах. Кроме того, если параметры распределения неизвестны заранее, то имеется еще одно ограничение, обусловленное подгонкой распределения к выборке. Если по выборке определяются f параметров распределения, то число степеней свободы составит k=y – f –1.
|
|
|
Область принятия гипотезы Н 0 определяется условием c 2£ c 2(k;a), где c 2(k;a) – критическая точка распределения хи-квадрат с уровнем значимости a. Вероятность ошибки первого рода равна a, вероятность ошибки второго рода четко определить нельзя, потому что существует бесконечно большое множество различных способов несовпадения распределений. Мощность критерия зависит от количества разрядов и объема выборки. Критерий рекомендуется применять при n> 200, допускается применение при n> 40, именно при таких условиях критерий состоятелен (как правило, отвергает неверную нулевую гипотезу).
Методы изучения сезонных колебаний в рядах динамики.
.
Сезонными колебания называются более или
менее устойчивые внутригодовые колебания уровня развития соц.эк. явления.
Сезонные колебания наблюдаются в различных видах эк. деятельности: с/х
строительстве, торговли и др. Значение стат. изучения сезонных колебаний
состоит в том, что получаемые при анализе колич. харак. Отображают специфику
развития изучаемых явлений по месяцам и кварталам годового цикла, что
необходимо для показания закономерности развития изучаемых явлений прогноз.
явл. и разработки мер по управл. и развития во времени. При стат. изучении
сезонных колебаний решаются две взаимосвязанных задачи: 1)выявление специфики
|
|
|
развития во внутригодовой динамики 2)измерение сезонных колебаний изучаемого
явления с построения модели сезонной волны. Для выявления сезонных колебаний
обычно анализ. Мес. И квартальные данные за несколько лет (что бы исключить
случайные условия одного года) Измерение сезонных колебаний осуществляется с
помощью расчета индексов сезонности которые показыв во сколько раз фактический
уровень ряда в может или интервал времени t больше среднего уровня или уровня
вычисленного по уравнению тенденции. Методика расчета индексов сезонности
различна она зависит от характера основной тенденции ряда динамики. Методы
расчета 1)Для рядов внутригодовой динамики не содержащих ярко-выраженной
тенденции в развитии расчет производится по империческим данным без их
предварительного выравнивания, для каждого месяца расчит средняя величина
уровня (за 3 года) затем из них вычисляется среднемесячный уровень для всего
ряда и в заключении определяется процентное отношение средних для каждого мес.
к общему среднемес. Уровню ряда. Индексы сезонности рассчитываются по формуле:
Уs=y`i/y` *100% где y`i – среднее значение уровней ряда за одноименные
внутригодичные периоды времени. y` - общая средняя для всех внутрегодичных
периодов. 2)Для рядов внутрегодовой динамики с ярко выраженной тенденцией
развития прежде чем вычислять сезонную волну имеперич. Данные должны быть
обработаны, чтобы была выявлена общая тенденция. Обычно производиться
аналитическое выравнивание, затем фактические данные выражаются в процентах к
выровненной, при этом ход решения след: а)для каждого мес (квартала) вычисл.
Выровненные уровни б)определяются отношения фактических мес. (квартальных
данных) yi(итое) соотв. Выравненым данным yt в %: yi=yi/yt * 100% в)Находятся
средние арифметические и с процентных соотношений расчитанных по одноименным
периодам в процентах: y`i = y1+y2+...+yn/n n- число одноименных периодов.
Таким образом в общем виде формула расчета индексов сезонности имеет вид: y =
∑yi/yt * 100% /n где yi- фактические исходные уровни динам. за отдельные
периоды, n-число лет. Совокупность рассчитанных индексов сезонности
характеризует сезонную волну для её наглядного представления начисленные
|
|
|
индексы связанности изображают виде графика.
При анализе рядов динамики важное значение имеет выявление сезонных колебаний. Этим колебаниям свойственны более или менее устойчивые изменения уровней ряда по внутригодовым периодам: месяцам, кварталам. Для выявления сезонных колебаний обычно анализируются месячные и квартальные уровни ряда динамики за год или за несколько лет. При изучении сезонных колебаний используются специальные показатели – индексы сезонности (IS). Способы определения индексов сезонности различны; они зависят от характера основной сезонности ряда динамики.
Для ряда внутригодовой динамики, в которой основная тенденция роста незначительна (или она не наблюдается совсем), изучение сезонности основано на методе постоянной средней: являющейся средней из всех рассматриваемых уровней. Самый простой способ заключается в следующем: для каждого года рассчитывается средний уровень, а затем с ним сопоставляется (в процентах) уровень каждого месяца. Это процентное отношение обычно именуется индексом сезонности:  .
.
При наличии ярко выраженной тенденции к увеличению или уменьшению уровней из года в год применимы другие способы измерения сезонных колебаний, в частности индексы сезонности определяются на основе методов, которые позволяют исключить влияние тенденции роста (падения).
При использовании способа аналитического выравнивания ход вычислений следующий:
1. вычисляют для каждого месяца (квартала) выравненные уровни по соответствующему аналитическому уравнению на момент времени t;
2. берут отношение фактических месячных (квартальных) данных (yi) к соответствующим им выравненным данным в процентах:  ;
;
3. находят среднюю из этих отношений для одноименных месяцев (кварталов) в процентах:
 ,
,
где n – число одноименных месяцев;
1. из полученных 12 помесячных относительных величин ( ) вычисляют общий среднемесячный уровень (
) вычисляют общий среднемесячный уровень ( );
);
2. определяют индексы сезонности по формуле  или
или 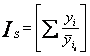 : n
: n
где  - исходные уровни ряда;
- исходные уровни ряда;
 - выравненные (теоретические) уровни ряда;
- выравненные (теоретические) уровни ряда;
n – число годовых периодов.
|
|
|
|
|
|


