 |
Понятие корреляционной зависимости и ее направленности
|
|
|
|
Будем говорить, что между двумя признаками Х и У существует корреляционная зависимость (взаимосвязь), при которой с изменением одного признака изменяется и другой, но каждому значению признака Х могут соответствовать разные, заранее непредсказуемые значения признака У, и наоборот.
Для различия направленности влияния одного признака на другой введены понятия положительной и отрицательной связи.
Если с увеличением (уменьшением) одного признака в основном увеличиваются (уменьшаются) значения другого, то такая корреляционная связь называется прямой или положительной.
Если с увеличением (уменьшением) одного признака в основном уменьшаются (увеличиваются) значения другого, то такая корреляционная связь называется обратной или отрицательной.
Корреляционной связью называют важнейший частный случай статистической связи, состоящий в том, что разным значениям одной переменной соответствуют различные средние значения другой. С изменением значения признака х закономерным образом изменяется среднее значение признака у; в то время как в каждом отдельном случае значение признака у (с различными вероятностями) может принимать множество различных значений.
Если же С изменением значения признака х среднее значение признака у не изменяется закономерным образом, но закономерно изменяется другая статистическая характеристика (показатели вариации, асимметрии, эксцесса и т.п.), то связь является не корреляционной, хотя и статистической.
Статистическая связь между двумя признаками (переменными величинами) предполагает, что каждый из них имеет случайную вариацию индивидуальных значений относительно средней величины. Если же такую вариацию имеет лишь один из признаков, а значения другого являются жестко детерминированными, то говорят лишь о регрессии, но не о статистической (тем более корреляционной) связи. Например, при анализе динамических рядов'можно измерять регрессию уровней ряда урожайности (имеющих случайную колеблемость) на номера лет. Но нельзя говорить о корреляции между ними и применять показатели корреляции с соответствующей им интерпретацией
|
|
|
Корреляция (от позднелат. correlatio - соотношение) - статическая мера связи двух или более признаков; коэффициент линейной корреляции характеризует знак и величину этой связи; чем выше величина коэффициента линейной корреляции, тем больше сходство сопоставляемых рядов данных.
1) взаимная связь, взаимозависимость, соотношение предметов или понятий;
2) статистическая мера связи, равная ковариации стандартизованных переменных;
3) в математической статистике - вероятностная или статистическая зависимость. В отличие от функциональной зависимости корреляция возникает тогда, когда зависимость одного из признаков от другого осложняется наличием ряда случайных факторов.
Корреляция - 1) термин, применяемый в различных областях науки и техники для обозначения взаимозависимости, взаимного соответствия, соотношения понятий, предметов, функций и т.д.; 2) статистическая мера связи, равная ковариации стандартизованных переменных; 3) взаимосвяз (взаимовлияние) двух данных единиц друг на друга (например, корреляция между признаками).
59. Прогнозирование на основе рядов динамики.
Процесс прогнозирования, опирающийся на статистические методы, распадается на два этапа. Первый, индуктивный, заключается в обобщении данных, наблюдаемых за более или менее продолжительный период времени, и в представлении соответствующих статистических закономерностей в виде модели. Статистическую модель получают или в виде аналитически выраженной тенденции развития, или же в виде уравнения зависимости от одного или нескольких факторов-аргументов. В ряде случаев – при изучении сложных комплексов экономических показателей – прибегают к разработке так называемых взаимозависимых систем уравнений, состоящих в основном опять-таки из уравнений, характеризующих статистические зависимости. Процесс построения и применения статистической модели для прогнозирования, какой бы вид последняя не имела, обязательно включает выбор формы уравнения, описывающего динамику или взаимосвязь явлений, и оценивание его параметров с помощью того или иного метода. Второй этап, собственно прогноз, является дедуктивным. На этом этапе на основе найденных статистических закономерностей определяют ожидаемое значение прогнозируемого признака.
|
|
|
Следует подчеркнуть, что полученные результаты не могут рассматриваться как нечто окончательное. При их оценке и использовании должны приниматься во внимание факторы, условия или ограничения, которые не были учтены при разработке статистической модели, должна осуществляться корректировка обнаруженных статистических характеристик в соответствии с ожидаемым изменением обстоятельств их формирования. Короче говоря, найденные с помощью статистических методов прогностические оценки являются важным материалом, который, однако, должен быть критически осмыслен. При этом главным является учет возможных изменений в самих тенденциях развития экономических явлений и объектов.
51. Ряд динамики, хронологический ряд, динамический ряд, временной ряд – это последовательность упорядоченных во времени числовых показателей, характеризующих уровень развития изучаемого явления. Всякий ряд динамики включает, следовательно, два обязательных элемента: во-первых, время и, во-вторых, конкретное значение показателя, или уровень ряда. Ряды динамики различаются по следующим признакам.
1. По времени – моментные и интервальные ряды. Интервальный ряд динамики – последовательность, в которой уровень явления относится к результату, накопленному или вновь произведенному за определенный интервал времени. Таковы, например, ряды показателей объема продукции по месяцам года, количества отработанных человеко-дней по отдельным периодам и т.д. Если же уровень ряда показывает фактическое наличие изучаемого явления в конкретный момент времени, то совокупность уровней образует моментный ряд динамики. Примерами моментных рядов могут быть последовательности показателей численности населения на начало года, величины запаса какого-либо материала на начало периода и т.д. Важное аналитическое отличие моментных рядов от интервальных состоит в том, что сумма уровней интервального ряда дает вполне реальный показатель – общий выпуск продукции за год, общие затраты рабочего времени, общий объем продаж акций и т.д., сумма же уровней моментного ряда, хотя иногда и подсчитывается, но реального содержания, как правило, не имеет.
|
|
|
2. По форме представления уровней – ряды абсолютных, относительных и средних величин
3. По расстоянию между датами или интервалам времени выделяют полные и неполные хронологические ряды.
Полные ряды динамики имеют место, когда даты регистрации или окончания периодов следуют друг за другом с равными интервалами. Это равноотстоящие ряды динамики. Неполные – когда принцип равных интервалов не соблюдается
Чтобы о развитии явления можно было получить представление при помощи числовых уровней, при составлении ряда динамики должны приводиться в сопоставительный вид.
Статистические данные должны быть сопоставимы по территории, кругу охватываемых объектов, единицам измерения, времени регистрации, ценам, методологии расчета. Сопоставимость по территории означает, что данные по странам и регионам, границы которых изменились, должны быть пересчитаны в старых пределах. Сопоставимость по кругу охватываемых объектов означает сравнение совокупностей с равным числом элементов. Территориальная и объемная сопоставимость обеспечивается смыканием рядов динамики, при этом либо абсолютные уровни заменяются относительными, либо делается пересчет в условные абсолютные уровни. Не возникает особых сложностей при обеспечении сопоставимости данных по единицам измерения; стоимостная сравнимость достигается системой сопоставимых цен.
|
|
|
Числовые уровни рядов динамики должны быть упорядоченными во времени. Не допускается анализ рядов с пропусками отдельных уровней, если же такие пропуски неизбежны, то их восполняют условными расчетными значениями.
К составлению рядов динамики предъявляются следующи требования.
1. Периодизация развития, т. е. расчленение его во временна однородные этапы, в пределах которых показатель подчиняете одному закону развития. Это, по существу, типологическа группировка во времени.
Методами периодизации являются:
• исторический метод, когда периодизация осуществляется н основе «узаконенной» структуры динамики, при этом обращаю внимание на значимые даты и события, а именно: время приняти управленческих решений по данному показателю, смен хозяйственного механизма, смену руководства, войны и т. i Недостаток этого метода в том, что точные временные границ периодов путем теоретического анализа удается получить край редко;
• метод параллельной периодизации: предполагается, что сущест вует показатель X, которому соответствует динамический ряд Xt определяющий поведение исследуемого показателя У, тогда в рол однокачественных периодов развития У можно взять периоды X.
Рассмотрим, например, динамику показателей X и У:
Периоды однокачественной динамики показателей X лег выделить: это 1981—1985 и 1986—1989 гг. Линейный коэффицие корреляции между этими рядами очень высок: R 0,995. Так-образом, можно считать, что ряд Xполностью определяет значен уровней ряда К Теперь, если предстоит качественный скач показателя X, то с очень большой степенью вероятности мож ожидать аналогичных изменений показателя У. В качест недостатка метода параллельной периодизации следует отмети сложности в нахождении Х детерминирующего показателя. Бол того, во многих случаях такой параметр вообще невозможно най"" так как он должен обладать весьма редкими свойствами — связью анализируемым показателем и, статейное, неоспоримыми временным границами периодов;
• методы многомерного статистического анализа. Част требуется выделить однокачественные периоды в развитии явлени или процессов, таких, например, как здоровье населения, развитие сельскохозяйственного производства и др., получить адекватное отображение которых с помощью одного лишь показателя трудно. Очевидно, что для эквивалентного описания столь сложного, интегрированного явления, как здоровье, нельзя ограничиться комплексными показателями смертности, продолжительности жизни, заболеваемости. Необходима система показателей, или комплексный хронологический ряд. Преимущества системы показателей очевидны:
|
|
|
—учитывается многообразие аспектов явления;
— амортизируется искажающее воздействие недостоверных и меточных статистических данных;
— наличие множества показателей повышает обоснованность статистических выводов, т. е. обеспечивается надежность их жстраполяции.
Идеальным выходом является использование множества показателей, включающего все характеристики процесса. Однако JTO не всегда возможно по разным причинам и чаще всего вследствие недоступности статистической информации. На основе комплексных динамических рядов (системы показателей) периодизация реализуется методом многомерной средней и методами факторного пнализа.
Однокачественность уровней временного ряда означает, что в пределах всего изучаемого периода, к которому относятся уровни, должна быть проведена типологическая группировка. После выделения однородных групп можно использовать и анализировать уровни ряда. Это требование формулируется как обеспечение сравнимости по структуре совокупности, для чего обычно применяется стандартная, нормативная структура.
2. Сопоставимость статистических данных — по территории, кругу охватываемых объектов, единицам измерения, времени регистрации, ценам, методологии расчета.
3. Соответствие величины временных интервалов инте сивности изучаемых процессов. Чем больше вариация уровней времени, тем чаще следует делать замеры. Соответственно дл стабильных процессов интервалы можно увеличить. Так, перепис населения достаточно проводить один раз в десять лет; уч национального дохода, урожая — раз в год, ежедневно регистр руются курсы покупки и продажи валют, ежечасно — температу воздуха и т. п.
4. Упорядоченность числовых уровней рядов динамики времени. Не допускается анализ рядов с пропусками отдельн уровней; если же такие пропуски неизбежны, то их восполня" условными расчетными значениями.
52.
Основные гипотезы о средних величинах следующие: гипотезы о значении генеральной средней (при известной генеральной дисперсии или при неизвестной генеральной дисперсии); гипотезы о равенстве генеральных средних нормально распределенных сово-купностей (при известных генеральных дисперсиях, при неизвестных равных генеральных дисперсиях, при неизвестных неравных генеральных дисперсиях).
Первая задача чаще всего решается при неизвестной генеральной дисперсии. Испытуемая гипотеза Н0: μ = μ0, альтернативная гипотеза Н1: μ? μ0. Испытание гипотезы проводят с помощью t- критерия. При большом числе наблюдений критическое значение критерия определяется по таблице интеграла вероятностей, при малом - по таблице распределения Стьюдента с заданным уровнем значимости и числом степеней свободы, п — 1.
Если испытуемая гипотеза Н0: μ = а, то фактическое значение критерия представляет отношение оцениваемой разности к средней возможной ошибке выборочной средней.
, (7.36)
где 
- при большой выборке;
- при малой выборке.
Если tфакт > tкрит, Н0 не отклоняется, если tфакт < tкрит, H0 отклоняется.
Гипотеза о равенстве средних может рассматриваться как гипотеза о связи, если сопоставляются средние величины, обусловленные действием какого-либо фактора. Например, сравнивается средняя заработная плата рабочих двуную плату.
Рассмотрим решение этой задачи при условии, что генеральные дисперсии неизвестны, но принимаются равными. При сравнении средних величин выдвигается гипотеза, что обе выборки принадлежат одной и той же генеральной совокупности со средней μ и дисперсией σ2.
При неизвестной генеральной дисперсии формула t-критерия имеет вид:
. (7.37)
Поскольку s21 и s22 рассматриваются как выборочные оценки общей дисперсии σ2, то формула (7.37) может быть записана так:
, (7.38)
где x?1, x?2 - выборочные средние; s2 - выборочная оценка общей дисперсии;
. (7.39)
Гипотеза H0 отклоняется, если 
Для анализа рядов динамики применяется сравнительный анализ, для того, чтобы выяснить какое явление развивается быстрее. Если сравниваются одноименные величины, то можно сопоставлять как абсолютные значения, так и относительные. Если производится сравнительный анализ разноименных явлений, то сравнивать можно только относительные величины. Для этого определяют базисные темпы роста к какой-либо единой базе сравнения.
Такой прием называется приведение рядов динамики к общему основанию. Выявление основной тенденции динамики. При изучении динамики любого из явлений, главной задачей анализа ставится выявление основной тенденции в развитии. Количественная характеристика явления в динамике многих факторов и их развитии зависит от этих факторов. Пример, сезонные колебания.
Для этого используют сглаживание рядов динамики по методу скользящей средней или по методу аналитического выравнивания уровней ряда динамики. Метод аналитического выравнивания ряда динамики по прямой Если фактические уровни ряда динамики нанести на график, то получим ломаную линию, которая будет отражать как основные тенденции в развитии, так и отклонения от них, вызванные сезонными колебаниями или другими факторами.
Чтобы выявить тенденцию необходимо выровнять ломаную линию, в основе выравнивания лежит теоретический анализ сущности данного явления и законы его развития. Следовательно, задача сводится к тому, чтобы фактические уровни ряда динамики (у) заменить теоретическими уровнями ряда.
Прямая, выравнивающая ряд должна проходить в максимальной близости от фактических уровней ряда, т.е. сумма квадратов отклонений должна быть наименьшей.
При изучении рядов динамики перед статистикой стоят следующие задачи: охарактеризовать интенсивность развития явления от периода к периоду (от даты к дате), а также среднюю интенсивность развития за исследуемый период, изучить сезонные колебания, выявить основную тенденцию в развитии явления, осуществить прогноз развития на будущее.
Для изучения интенсивности изменения уровней ряда во времени исчисляются следующие показатели динамики:
абсолютные приросты;
коэффициенты роста;
темпы роста;
темпы прироста;
абсолютные значения одного процента прироста.
Перечисленные показатели динамики можно исчислять с переменой или постоянной базой. Если производится сравнение каждого уровня с предыдущим уровнем, то получают показатели динамики с переменной базой (цепные показатели динамики). Если каждый уровень сравнивается с начальным уровнем или каким-то другим, принятым на базу сравнения, то получают показатели динамики с постоянной базой (базисные показатели динамики). База сравнения должна выбираться обоснованно, в зависимости от экономических особенностей явления и задач исследования.
Методы расчета показателей динамики представлены в табл. 24.1. Они одинаковы и для моментных, и для интервальных рядов.
При расчете показателей приняты следующие условные обозначения:
— уровень любого периода (кроме первого), называемый Уровнем текущего периода;
— уровень периода, предшествующего текущему;
— уровень, принятый за постоянную базу сравнения (часто начальный уровень).
Для характеристики интенсивности развития за длительный период рассчитываются средние показатели динамики. Метод их расчета представлен в табл. 24.2.
При написании формул приняты следующие условные обозначения: у\, у2, -, Уп — уровни последовательных периодов (дат); п — число уровней ряда; t — продолжительность периода, в течение которого уровень не изменялся.
54.
Одним из основных приложений критерия χ2 является его использование при анализе таблиц сопряженности двух переменных для установления факта наличия и уровня значимости взаимосвязи. Как правило, критерий у2 применяется для анализа таблиц сопряженности номинальных признаков, однако" он может быть использован и при анализе взаимосвязи порядковых или интервальных (количественных) переменных, несмотря на то, что для последних. случаев существуют более мощные тесты.
Рассмотрим общий случай - таблицу сопряженности двух переменных размером r × s. Обозначим:
nij - наблюдаемая частота (число объектов) в ячейке (ij) таблицы, так называемая фактическая клеточная частота; n?ij - теоретически ожидаемая (по Н0) частота в этой ячейке, i = 1, 2,..., r, j = 1, 2,..., s; r - число строк, s - число столбцов.
- сумма по j-й строке маргинальные частоты
- сумма по j-у столбцу (7.31)
- общее число объектов или объем выборки.
В этом случае испытуемая гипотеза Н0: nij? n?ij или Н0: χ2 =0, альтернативная гипотеза H1: nij? n?ij. Критерий χ2 для проверки Н0 имеет вид:
. 
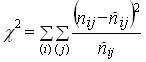(7.32)
Расчет теоретически ожидаемых частот в ячейках таблицы сопряженности должен производиться, как мы уже указывали выше, в предположении справедливости нулевой гипотезы. Нуль-гипотеза (Н0) в данном случае есть предположение о статистической независимости рассматриваемых переменных. Как известно из теории вероятностей, две случайные величины (события) являются статистически независимыми, если вероятность их совместной реализации равна произведению вероятностей реализации каждой из них по отдельности, т. е.
, 
где
В нашем случае выборочными оценками соответствующих вероятностей π будут являться величины р(хi, хj) = пij/п,
и поэтому расчет теоретически ожидаемой по Н0 частоты п?ij следует производить по формуле
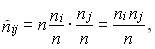(7.33)
т. е. произведение итогов по столбцу и строке, деленное на общий объем данных.
Если подставить выражение п?ij в формулу (7.32), то получим
(7.34)
Используя эту формулу, мы можем находить эмпирические значения критерия χ2 без промежуточного вычисления теоретических частот в явном виде.
Очевидно, что для определения эмпирического значения критерия χ2 нет необходимости рассчитывать все s теоретических частот в каждой строке, а достаточно найти лишь s - 1 значение частоты в r - 1 строке, так как оставшиеся частоты могут быть получены как разности между маргинальными суммами эмпирических частот и суммами известных теоретических частот, т. е. значения теоретических частот в последних строке и столбце таблицы всегда полностью детерминированы. Поэтому число степеней свободы для r × s таблицы сопряженности равно:
d.f.= (r - 1) (s -1). (7.35)
Заметим, что для таблицы 2×2 число степеней свободы равно 1.
В таблице распределения статистики χ2d.f.α приведены значения этой величины для различных уровней значимости при различных числах степеней свободы (см. приложение, табл. 4). Например, на уровне α = 0,01 для d.f. = 1 мы находим χ2 = 10,827. Это означает, что равное или большее значение этой величины χ2 может встретиться только один раз из тысячи при условии, что все сделанные допущения (нуль-гипотеза) справедливы. Другими словами, если выполняется предложение об отсутствии взаимосвязи между переменными, то крайне маловероятно (Р < 0,001), что наблюдаемые и ожидаемые частоты будут отличаться настолько, что фактическая величина χ2 будет равной или большей 10,827. Если же χ2ф ≥ χ2d.f.α, то гипотеза Н0 на данном уровне значимости а может быть отвергнута.
Вероятность того, что, отвергая нулевую гипотезу, мы совершаем ошибку (первого рода), которая численно равна уровню значимости о., задаваемому при проверке гипотезы.
Интерпретация χ2 теста зачастую усложняется, когда в таблице сопряженности имеются ячейки с нулевыми значениями наблюдаемых частот. Дело в том, что если пара (хi, хj) значений переменных не наблюдалась в выборке, то это может означать, что объем выборки не столь велик, чтобы зафиксировать такую редкую комбинацию, либо что данная комбинация невозможна по каким-то объективным причинам. В последнем случае действительное число степеней свободы анализируемой системы меньше числа степеней свободы таблицы сопряженности, на основании которого произведена оценка уровня значимости χ2 теста.
Корректировка применения χ2 теста возможна лишь в том случае, если эмпирические данные, наполняющие таблицу сопряженности, есть результаты независимой случайной выборки относительно большого объема п. Последнее требование вызвано тем, что выборочное распределение χ2 аппроксимирует табличное распределение статистики χ2 только при больших п. Естественно, возникает вопрос о том, насколько велико должно быть п, чтобы иметь возможность использовать данный тест. Ответ на этот вопрос зависит от числа ячеек и величин маргинальных сумм. Вообще говоря, чем меньше число ячеек и чем более близки между собой по величине маргиналы, тем меньше может быть п. Существует, однако, практическое число, позволяющее оценить снизу по п диапазон возможного применения критерия χ2: если в данной таблице сопряженности любая из теоретических ожидаемых частот п?ij в ячейке (i, j) не больше 5, то рекомендуется произвести, если это возможно, модификацию таблицы либо воспользоваться другим критерием.
В общем случае корректировка таблицы размера r? s затруднительна. Практика показала, что если число ячеек велико, а ожидаемые частоты, равные или меньше пяти, встречаются лишь в одной-двух ячейках, то проведение корректировки нецелесообразно; во всех иных случаях разумной альтернативой является объединение категорий (градаций) с тем, чтобы элиминировать подобные ячейки. Естественно, такое объединение должно быть таким, чтобы получаемая в результате комбинация не была содержательно бессмысленной.
В социально-экономических исследованиях, как правило, установление факта наличия связи между переменными не самоцель. Установив наличие связи, исследователь должен измерить ее силу (тесноту) с тем, чтобы иметь возможность сравнивать взаимосвязи между различными характеристиками, выделять наиболее сильные из них
55.
Одна из важнейших задач статистики- определение в рядах динамики общей тенденции развития.
Основной тенденцией развития называется плавное и устойчивое изменение уровня во времени, свободное от случайных колебаний. Задача состоит в выявлении общей тенденции в изменении уровней ряда, освобожденной от действия различных факторов.
Изучение тренда включает два основных этапа:
ряд динамики проверяется на наличие тренда;
производится выравнивание временного ряда и непосредственно выделение тренда с экстраполяцией полученных результатов.
С этой целью ряды динамики подвергаются обработке методами укрупнение интервалов, скользящей средней и аналитического выравнивания:
Метод укрупнения интервалов.
Одним из наиболее элементарных способов изучения общей тенденции в ряду динамики является укрупнение интервалов. Этот способ основан на укрупнении периодов, к которым относятся уровни ряда динамики. Например, преобразование месячных периодов в квартальные, квартальных в годовые и т.д.
Метод скользящей средней.
Выявление общей тенденции ряда динамики можно произвести путем сглаживания ряда динамики с помощью скользящей средней.
Скользящая средняя- подвижная динамическая средняя, которая рассчитывается по ряду при последовательном передвижении на один интервал, то есть сначала вычисляют средний уровень из определенного числа первых по порядку уровней ряда, затем- средний уровень из такого же числа членов, начиная со второго. Таким образом, средняя как бы скользит по ряду динамики от его начала к концу, каждый раз отбрасывая один уровень в начале и добавляя один следующий.
При этом посредством осреднения эмпирических данных индивидуальные колебания погашаются, и общая тенденция развития явления выражается в виде некоторой плавной линии (теоретические уровни). И так, суть метода заключается в замене абсолютных данных средними арифметическими за определенные периоды.
Скользящая средняя обладает достаточной гибкостью, но недостатком метода является укорачивание сглаженного ряда по сравнению с фактическим, что ведет к потери информации. Кроме того, скользящая средняя не дает аналитического выражения тренда.
Период скользящей может быть четным и нечетным. Практически удобнее использовать нечетный период, так как в этом случае скользящая средняя будет отнесена к середине периода скольжения. Скользящие средние с продолжительностью периода, равной 3, следующие:
; 
; 
и т.д.
Полученные средние записываются к соответствующему срединному интервалу.
Особенность сглаживания по четному числу уровней состоит в том, что каждая из численных (например, четырехчленных) средних относится к соответствующим промежуткам между смежными периодами. Для получения значений сглаженных уровней соответствующих периодов необходимо произвести центрирование расчетных средних.
Недостатком способа сглаживания рядов динамики является то, что полученные средние не дает теоретических рядов, в основе которых лежала бы математически выраженная закономерность.
Метод аналитического выравнивания.
Более совершенным приемом изучения общей тенденции в рядах динамики является аналитическое выравнивание. При изучении общей тенденции методом аналитического выравнивания исходят из того, что изменения уровней ряда динамики могут быть с той или иной степенью точности приближения выражены определенными математическими функциями. Вид уравнения определяется характером динамики развития конкретного явления. Логический анализ при выборе вида уравнения может быть основан на рассчитанных показателях динамики, а именно:
если относительно стабильны абсолютные приросты (первые разности уровней приблизительно равны),, сглаживание может быть выполнено по прямой;
если абсолютные приросты равномерно увеличиваются (вторые разности уровней приблизительно равны), можно принять параболу второго порядка;
при ускоренно возрастающих или замедляющихся абсолютных приростах - параболу третьего порядка;
при относительно стабильных темпах роста- показательную функцию.
Для аналитического выравнивания наиболее часто используются следующие виды трендовых моделей: прямая (линейная), парабола второго порядка, показательная (логарифмическая) кривая, гиперболическая.
Цель аналитического выравнивания- определение аналитической или графической зависимости. На практике по имеющемуся временному ряду задают вид и находят параметры функции, а затем анализируют поведение отклонений от тенденции. Чаще всего при выравнивании используются следующие зависимости; линейная, параболическая и экспоненциальная.
После выяснения характера кривой развития необходимо определить ее параметры, что можно сделать различными методами:
решением системы уравнений по известным уровням ряда динамики;
методом средних значений (линейных отклонений), который заключается в следующем: ряд расчленяется на две примерно равные части, и вводятся преобразования, чтобы сумма выровненных значений в каждой части совпала с суммой фактических значений, например, в случае выравнивания прямой линии 
;
выравниванием ряда динамики с помощью метода конечных разностей;
методом наименьших квадратов: это некоторый прием получения оценки детерминированной компоненты, 
характеризующих тренд или ряд изучаемого явления.
Во многих случаях моделирование рядов динамики с помощью полиномов или экспоненциальной функции не дает удовлетворительных результатов, так как в рядах динамики содержатся заметные периодические колебания вокруг общей тенденции. В таких случаях следует использовать гармонический анализ.
Для менеджера предпочтительно применение именно этого метода, поскольку он определяет закон, по которому можно достаточно точно спрогнозировать значения уровней ряда. Однако его применение требует достаточных знаний в области высшей математики и математической статистики.
|
|
|
