 |
Исследование турбулентной фильтрации
|
|
|
|
Цель работы- экспериментально изучить законы турбулентной фильтрации жидкости через пористую среду.
Теоретические сведения
Как известно, режим турбулентной фильтрации наступает при выполнении условия:
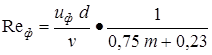>7…9, (8.1)
где Reф –фильтрационное число Рейнольдса;
u ф - скорость фильтрации;
d -средний размер частиц пористой среды;
n - коэффициент кинематической вязкости жидкости;
m - пористость.
При турбулентной фильтрации нарушается закон Дарси и наблюдается нелинейная зависимость скорости фильтрации от пьезометрического уклона:
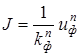
(8.2)
(8.3)
где а, b, n - экспериментальные коэффициенты.
где k ф- коэффициент фильтрации.
При малых скоростях фильтрации, т.е. при Reф < 7, законы (8.2) и (8.3) вырождаются в закон Дарси. При этом n = 1, b =0.
При квадратичном законе сопротивление (Reф > 10000) уравнение (8.2) принимает вид
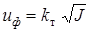(8.4)
где k т - коэффициент турбулентной фильтрации, определяемой по формуле С.В. Избаша, см/с:
k т = С ф m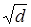 
(8.5)
Для крупнозернистых грунтов
, 
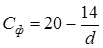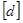= см (8.6)
Описание установки
Установка показана на рисунке 6.2. Порядок выполнения данной работы аналогичен порядку выполнения лабораторной работы №7. Изменяя краном напор жидкости, провести 5-10 опытов при различных расходах, когда условие 8.1. выполняется в каждом опыте. Результаты измерений занести в табл. 8.1.
Таблица 8.1 – Результаты измерений
| Но-мер опы-та | Площадь сечения w, м2 | Средний диаметр частиц d ч, м | Темпера-тура жидкости t 0, 0C | Расход Q, м3/с | Скорость фильтра-ции u ф, м/с | Пьезомет-рический уклон J, м/м |
Обработка результатов экспериментов
|
|
|
Определяют расход жидкости в каждом опыте (объемным способом):
Qi = 
.
По величине Qi находят скорость фильтрации
u фi =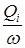 
.
Зная средний диаметр частиц пористой среды d ч и температуру жидкости t 0, проверяют условие турбулентности (8.1.).
Используя экспериментальные значения пьезометрического уклона J 
, методом наименьших квадратов определяют искомые коэффициенты a, b, n.
Метод наименьших квадратов
Метод построен на подборе аналитической зависимости, наилучшим образом описывающей данные. Аналитическая зависимость подбирается исходя из условия минимума функционала:
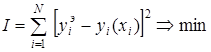(8.7)
Для условий данной лабораторной работы функционал (8.7) записывают в виде
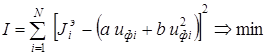(8.8)
Условием минимума функционала является равенство нулю частных производных функционала по искомым величинам:
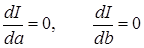(8.9)
Взяв производные, получим:
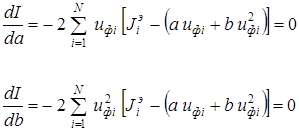(8.10)
Решив систему уравнения (8.10) относительно искомых a и b, n получим:
,
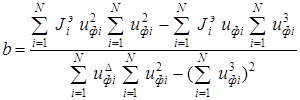(8.11)
.
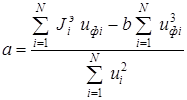Прологарифмировав уравнение (8.3) и воспользовавшись известным из лабораторной работы №7 значением коэффициента фильтрации k ф, аналогичным образом найдем числовое значение коэффициента:
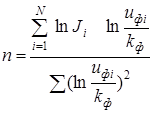/8.12/
Контрольные вопросы
1. Турбулентная фильтрация условия ее возникновения, закон турбулентной фильтрации.
2. Метод наименьших квадратов, его суть.
Лабораторная работа №9
Экспериментальное изучение свободной затопленной струи
Цель работы- экспериментально проверить зависимость осевой скорости турбулентной затопленной струи от расстояния вдоль оси для различных типов насадок.
Теоретические сведения
Струей называется поток жидкости (газа), не ограниченный какими либо твердыми поверхностями. Если струя данной жидкости (газа) движется в среде, представляющей собой ту же жидкость (газ), то такая струя считается затопленной.
Рассмотрим затопленную изометрическую струю, образовавшейся при продувании воздуха через насадку.
|
|
|
Вследствие турбулентного перемешивания движущихся частиц с окружающей средой, струя постепенно расширяется, что обуславливает увеличение расхода через поперечное сечение по мере удаления от места истечения и изменение скорости вдоль оси струи.
Внутри ядра струи (рис.9.1) осевая максимальная скорость не изменяется. Ядро окружено пограничным слоем, расширяющимся по мере его сужения.
О – плюс струи; ОО/ - ось струи; К/К- ядро струи; ОА, ОА, ОВ, ОВ- изотахи; 2 r 0- диаметр насадки; u 0- максимальная осевая скорость струи.
Рис. 9.1 - Схема течения в затопленной струе
Изотахи представляют собой линии равных относительных скоростей, т.е. в любой точке на них выполняется равенство:
, (9.1)
где w- средняя скорость струи вдоль оси ОХ.
Точка пресечение изотах – это полюс струи.
Полагая статическое давление в струе равным давлению в окружающей неподвижной среде, применим закон сохранения импульса для произвольного сечения w струи с сечением насадки w 0:
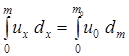, (9.2)
где m - масса жидкости (газа) протекающая через произвольное сечение струи;
u x – скорость струи вдоль оси ОХ;
d m- масса элементарной струйки в произвольном сечении, протекающая за 1 с;
m 0- масса жидкости (газа), протекающая через сечение насадки;
u 0- начальная скорость струи.
Учтем, что
(9.3)
После подстановки (9.3) в (9.2) получим:
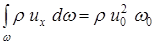(9.4)
Если затопленная струя вытекает из круглого отверстия радиуса r 0, то уравнение (9.4) приобретает вид
, (9.5)
где r s- радиус произвольного сечения струи w.
Введем безразмерные переменные 
и Vx= 
и перепишем уравнение (9.5) в виде
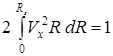(9.6)
Заменим в (9.6)
;
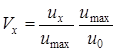
Получим
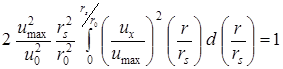(9.7)
где u max- мгновенное значение скорости на оси струи;
r s- значение радиуса сечения струи, соответствующему данному V max.
После вычисления интеграла (9.7) получим
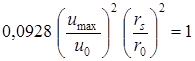
откуда с достаточной точностью приближения, учитывая, что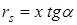 
, где a - угол между осью и границей распространения струи.
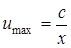
Значение постоянной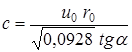 
можно определить опытным путем, чем и проверить правильность теоретических выкладок.
Описание установки
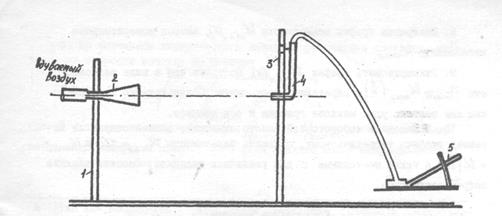
Установка представляет собой неподвижный кронштейн 1 (рис. 9.2.) со сменной насадкой 2 и подвижным кронштейном 3 с прикрепленной к нему трубкой Пито 4, которая соединена с микроманометром 5. Трубка Пито 4 перемещается в вертикальном и горизонтальном (осевом) направлениях, что позволяет исследовать распределение скоростей в данном поперечном сечении струи. Установка укомплектована тремя видами насадок: цилиндр, диффузор (с углом раскрытием 70) и конфузор.
|
|
|
|
Рис. 9.2. Схема экспериментальной установки для исследования
затопленной струи.
|
|
|
