Обработка результатов измерений.

ПРЯМЫЕ ИЗМЕРЕНИЯ

Работа химиков, физиков и представителей других естественно-научных профессий часто связана с выполнением количественных измерений различных величин. При этом возникает вопрос анализа достоверности получаемых значений, обработки результатов непосредственных измерений и оценки погрешностей расчетов, в которых используются значения непосредственно измеряемых характеристик (последний процесс также называется обработкой результатов косвенных измерений).

Для уменьшения влияния случайных ошибок обычно производят измерение величины несколько раз. Предположим, что мы измеряем некоторую величину x. В результате проведенных измерений мы получили значений величины:

 

x₁, x₂, x₃,... x_n. (2)

 

Этот ряд значений величины x получил название выборки. Имея такую выборку, мы можем дать оценку результата измерений. Величину, которая будет являться такой оценкой, мы обозначим 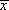. Но так как это значение оценки результатов измерений не будет представлять собой истинного значения измеряемой величины, необходимо оценить его ошибку. Предположим, что мы сумеем определить оценку ошибки Δx. В таком случае мы можем записать результат измерений в виде

 

х = 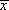± Δx (3)

Так как оценочные значения результата измерений 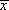и ошибки Δx не являются точными, запись (3) результата измерений должна сопровождаться указанием его надежности P. Под надежностью или доверительной вероятностью понимают вероятность того, что истинное значение измеряемой величины заключено в интервале, указанном записью (3). Сам этот интервал называется доверительным интервалом.

Например, измеряя длину некоторого отрезка, окончательный результат мы записали в виде

l = (8.34 ± 0.02) мм, (P = 0.95)

 

Это означает, что из 100 шансов – 95 за то, что истинное значение длины отрезка заключается в интервале от 8.32 до 8.36 мм.

Таким образом, задача заключается в том, чтобы, имея выборку найти оценку результата измерений 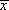, его ошибку Δx и надежность P.

 

Средней квадратичным отклонением результата измерения называется величина (в некоторой литературе обозначается как S)

 

(4)

 

Δx – абсолютная ошибка для данной доверительной вероятности (может обозначаться как )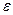

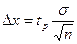(5)

Где t_p – коэффициент Стьюдента при соответствующей доверительной вероятности (таблица 1).

 

при заданном Р

 

Таблица 1

Коэффициенты Стьюдента
n	Значения Р
0.6	0.8	0.95	0.99	0.999
	1.376	3.078	12.706	63.657	636.61
	1.061	1.886	4.303	9.925	31.598
	0.978	1.638	3.182	5.841	12.941
	0.941	1.533	2.776	4.604	8.610
	0.920	1.476	2.571	4.032	6.859
	0.906	1.440	2.447	3.707	5.959
	0.896	1.415	2.365	3.499	5.405
	0.889	1.397	2.306	3.355	5.041
	0.883	1.383	2.262	3.250	4.781
	0.879	1.372	2.228	3.169	4.587
	0.876	1.363	2.201	3.106	4.437
	0.873	1.356	2.179	3.055	4.318
	0.870	1.350	2.160	3.012	4.221
	0.868	1.345	2.145	2.977	4.140
	0.866	1.341	2.131	2.947	4.073
	0.865	1.337	2.120	2.921	4.015
	0.863	1.333	2.110	2.898	3.965
	0.862	1.330	2.101	2.878	3.922
	0.861	1.328	2.093	2.861	3.883
	0.860	1.325	2.086	2.845	3.850
	0.859	1.323	2.080	2.831	3.819
	0.858	1.321	2.074	2.819	3.792
	0.858	1.319	2.069	2.807	3.767
	0.857	1.318	2.064	2.797	3.745
	0.856	1.316	2.060	2.787	3.725
	0.856	1.315	2.056	2.779	3.707
	0.855	1.314	2.052	2.771	3.690
	0.855	1.313	2.048	2.763	3.674
	0.854	1.311	2.045	2.756	3.659
	0.854	1.310	2.042	2.750	3.646
	0.851	1.303	2.021	2.704	3.551
	0.848	1.296	2.000	2.660	3.460
	0.845	1.289	1.980	2.617	3.373
∞	0.842	1.282	1.960	2.576	3.291

 

Пример:

Проводили измерения длины металлического бруска. Было сделано 10 измерений и получены следующие значения: 10 мм, 11 мм, 12 мм, 13 мм, 10 мм, 10 мм, 11 мм, 10 мм, 10 мм, 11 мм. Записать результат измерения при доверительной вероятности 0, 95

Решение:

= 10,8 (мм)

Находим среднее квадратичное отклонение

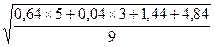= =1,033

По таблице для Р=0,95 и количества измерений n=10, t_p=2,262

0,74 (мм)

Ответ: P=0,95

Задачи:

 

1. Результаты многократного измерения длинны детали (мм) следующие: 80,003; 80.000; 79,998; 80.000; 79,998. Систематическая погрешность показаний составляет (+0,003 мм). Как правильно записать результаты измерений при доверительной вероятности Р=0,95 (относительная ширина доверительного интервала t при числе степеней свободы к=4 составит t=2,776) …

 

2. При многократном измерении температуры Т в производственном помещении получены значения в ⁰С: 20,4; 20,2; 20,0; 20,5; 19,7; 20,3; 20,4; 20,1. Укажите доверительные границы истинного значения температуры в помещении с вероятностью Р=0,95 (t_р=2,365).

 

3. При многократном измерении массы получены значения в кг: 98, 100, 97, 101, 99, 102, 103. Укажите доверительные границы для истинного значения массы с вероятностью Р=0,95 (t_р=2,45)

 

4. При многократном измерении отверстия получены отклонения от настроенного размера D в мкм: 0, +1, +2, +3, +1, -1. Как следует записать результат измерения при вероятности Р=0,982 коэффициент Стьюдента t_р=3,465.

 

5. При измерении усилия динамометр показывает 1000 Н. погрешность градуировки равна -50 Н. Среднее квадратичное отклонение показаний σ_F=10 Н. Укажите доверительные границы для истинного значения измеряемого усилия с вероятностью Р=0,9544 (t_p=2)

 

6. При многократном измерении силы F получены значения в Н: 403; 408; 410; 405; 406; 398; 406; 404. Укажите доверительные границы истинного значения силы с вероятностью Р=0,95 (t_p=2,365).

 

7. Амперметр с пределами измерений 0….10А показывает 8 А. Погрешность от подключения амперметра в цепь ∆_s=-0,2 А. Среднее квадратичное отклонение показаний прибора σ_I=0,3 А. Укажите доверительные границы истинного значения измеряемой силы тока в цепи с вероятностью Р=0,9544 (t_p=2)

 

8. Вольтметр показывает 230В. Среднее квадратичное отклонение показаний σ_U = 2 В. Погрешность от подключения вольтметра в цепь (изменение напряжения) равна -1 В. Чему равно истинное значение напряжения с вероятностью Р=0,9544 (t_p=2).

 

9. При многократном измерении длины L получены значения в мм: 30,2; 30,0; 30,4; 29,7; 30,3; 29,9; 30,2. Укажите доверительные границы истинного значения длины с вероятностью Р=0,98 (t_p=3,143)

 

10. При измерении температуры Т в помещении термометр показывает 26 ⁰С. Среднее квадратичное отклонение показаний σ_Т=0,3⁰С. Систематическая погрешность измерения ∆_s=+0,5⁰С. Укажите доверительные границы для истинного значения температуры с вероятностью Р=0,9973 (t_p=3)

 

11. При многократном измерении длины L получены значения в мм: 91; 90;95; 90; 93; 91; 94. Укажите доверительные границы истинного значения длины с вероятностью Р=0,99 (t_р=3,707)

 

12. Результаты многократного измерения твердости детали по шкале Роквела следующие: 32; 33; 35; 32; 34. Систематическая погрешность составляет (-1НRС мм). Как записать результата измерения при доверительной вероятности Р=0,95 (относительная ширина доверительного интервала t при числе степеней свободы k=4 составит t=2,8).

 

Косвенные измерения

Косвенное измерение – измерение, при котором значение физической величины определяют на основании результатов прямых измерений других физических величин, функционально связанных с искомой.

В большинстве экспериментов используют косвенные измерения. Исследуемую величину f определяют по результатам прямых измерений других физических величин, например, x,y,z,..., с которыми она связана заранее установленным функциональным математическим соотношением

f = f(x, y, z, …).

При косвенных измерениях:

1. Для каждой серии измерений величин, входящих в определение искомой величины, производится обработка в описанной выше последовательности. При этом для всех измеряемых величин задают одно и то же значение доверительной вероятности Р.

2. По заданной формуле находится среднее арифметическое косвенной искомой величины.

3. Определить среднее квадратичное отклонение совместного распределения, вычисляемое как корень из дисперсии, следует находить из выражения:

Пример. Без учета поправки на теплообмен подъем температуры в калориметре определяют как разность между конечной 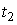и начальной температурами. После обработки опытных данных были получены следующие (округленные) результаты с соответствующими среднеквадратическими отклонениями:

t₁=25,10718⁰C, 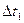=0,6*10^{-4 0}С

t₂=27,10739⁰C, =0,3*10^{-4 0}С

 

Результат косвенного измерения находим как разность соответствующих средних арифметических:

=27,10739-25,10718=2,00021⁰С

 

а среднеквадратическое отклонение результата:

 

Итог измерения: 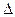t=(2,00021 0,00007)⁰C, P=0,6826

Здесь мы приняли t_P=1, что при нормальном распределении погрешностей измерений и достаточно большом числе их наблюдений соответствует доверительной вероятности 0.6826 нахождения подъема температуры в указанных пределах.

Задачи:

 

1. При испытании материала на растяжение измерением получены значения силы F=903 Н и диаметра стержня d=10 мм. Средние квадратичные отклонения погрешности измерений этих параметров: =5Н, =0,05 мм. Укажите доверительные границы для истинного значения напряжения с доверительной вероятностью Р=0,95 (t_p=1,96), если предел прочности определяется по формуле 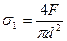. Значение погрешности округляется до одной значащей цифры.

2. Сопротивление нагрузки определяется по закону Ома . Показания Вольтметра U=100 В, Амперметра I=2А. Средние квадратичные отклонения показаний: вольтметра 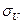=0,5В, амперметра =0,05 А. Доверительные границы истинного значения сопротивления с вероятностью Р=0,95 (t_p=1,96) равны…

⇐ Предыдущая123Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: