Системы счисления. Двоичная система счисления.

Двоичная система счисления — это позиционная система счисления с основанием 2. В этой системе счисления натуральные числа записываются с помощью всего лишь двух символов (в роли которых обычно выступают цифры 0 и 1).

Двоичная система используется в цифровых устройствах, поскольку является наиболее простой и соответствует требованиям:

• Чем меньше значений существует в системе, тем проще изготовить отдельные элементы, оперирующие этими значениями. В частности, две цифры двоичной системы счисления могут быть легко представлены многими физическими явлениями: есть ток — нет тока, индукция магнитного поля больше пороговой величины или нет и т. д.
• Чем меньше количество состояний у элемента, тем выше помехоустойчивость и тем быстрее он может работать. Например, чтобы закодировать три состояния через величину индукции магнитного поля, потребуется ввести два пороговых значения, что не будет способствовать помехоустойчивости и надёжности хранения информации.
• Двоичная арифметика является довольно простой. Простыми являются таблицы сложения и умножения — основных действий над числами.
• Возможно применение аппарата алгебры логики для выполнения побитовых операций над числами.

 

Преобразование двоичных чисел в десятичные.

При переводе числа из любой системы счисления в десятичную систему счисления нужно каждый символ этого числа умножить на основание системы счисления, в которой записано это число, в степени соответствующей положению символа в записи числа и все произведения сложить.

 

Например:

Переведём число 101100, 1011₂ из двоичной системы счисления в десятичную систему счисления:

101100, 101₂ = 1*2⁵ + 0*2⁴ + 1*2³ + 1*2² + 0*2¹ + 0*2⁰ + 1*2^-1 + 0*2^-2 + 1*2^-3 =
= 32 + 0 + 8 + 4 + 0 + 0 + 0,5 + 0 + 0,125 = 44, 625₁₀

 

Ещё один пример:

Допустим, вам дано двоичное число 110001. Для перевода в десятичное просто запишите его справа налево как сумму по разрядам следующим образом:

 

Можно записать это в виде таблицы следующим образом:

				+32	+16				+1

 

Точно так же, начиная с двоичной точки, двигайтесь справа налево. Под каждой двоичной единицей напишите её эквивалент в строчке ниже. Сложите получившиеся десятичные числа.
Таким образом, двоичное число 110001 равнозначно десятичному 49.

Преобразование методом Горнера

Для того, что бы преобразовывать числа из двоичной в десятичную систему данным методом, надо суммировать цифры слева-направо, умножая ранее полученный результат на основу системы (в данном случае 2). Например, двоичное число 1011011 переводится в десятичную систему так: 0*2+ 1 =1 >> 1*2+ 0 =2 >> 2*2+ 1 =5 >> 5*2+ 1 =11 >> 11*2+ 0 =22 >> 22*2+ 1 =45 >> 45*2+ 1 =91 То есть в десятичной системе это число будет записано как 91. Или число 101111 переводится в десятичную систему так: 0*2+ 1 =1 >> 1*2+ 0 =2 >> 2*2+ 1 =5 >> 5*2+ 1 =11 >> 11*2+ 1 =23 >> 23*2+ 1 =47 То есть в десятичной системе это число будет записано как 47

 

Преобразование десятичных чисел в двоичные.

Допустим, нам нужно перевести число 19 в двоичное. Вы можете воспользоваться следующей процедурой:

19 /2 = 9 с остатком 19 /2 = 4 c остатком 14 /2 = 2 с остатком 02 /2 = 1 с остатком 01 /2 = 0 с остатком 1

Итак, мы делим каждое частное на 2 и записываем в остаток 1 или 0. Продолжать деление надо пока в делимом не будет 1. Ставим числа из остатка друг за другом, начиная с конца. В результате получаем число 19 в двоичной записи (начиная с конца): 10011.

 

Двоичная арифметика.

Сложение чисел в двоичной системе счисления.

При сложении чисел в двоичной системе счисления, нужно использовать следующую таблицу сложения:

1 + 0 = 1

0 + 1 = 1

0 + 0 = 0

1 + 1 = 10

 

Например, сложим числа 1101111₂ и 1011101₂

 

Умножение чисел в двоичной системе счисления.

При умножении чисел в двоичной системе счисления, нужно использовать следующую таблицу умножения:

1 * 0 = 0

0 * 1 = 0

0 * 0 = 0

1 * 1 = 1

 

Например, перемножим числа 11111₂ и 101₂

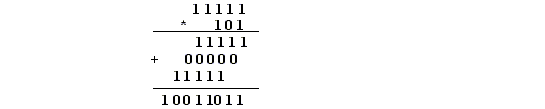
⇐ Предыдущая123

Поделиться:

Воспользуйтесь поиском по сайту: